概念
什么是算法?(内容都是出自大话数据结构)
算法其实就是我们读书的时候的阶梯方法,一个题目对应这多解。比如说最常见的高斯求和,你可以从1到100的一个个算。你也可以用高斯的解法去算。答案都能算出来。只是步骤的多或少而已。换到我们的计算机领域中什么是算法呢?范围大一点就是你写的代码都是算法。准确点就是你写的函数都是算法。例子
这就是一个算法,其他语言写也行,只是我刚好就用js,就用js写了。之后会用C
function a (n) {
let sum ;
for (let i = 0; i < n; i++) {
sum += i;
}
return sum;
}
算法的比较
为什么会出现算法的比较呢?
还是之前的问题,你的解法是不是最优解,是不是很快,是不是通俗易懂。这就出现比较了。也好比说同样是人为什么人家是资本,你是无产。为什么人家生下来就是包租公,你是打工人。哈哈,跑题了。回到我们的问题,上面我们写了一个常规的求和,这个算法看上去没什么问题,也能够完美的解决我们的问题。就很nice。有些数学好的同学就提出了那么麻烦,要我算100次我才不干呢。于是乎就想出了以下的解题思路。其实就是等差数列中的累加法。不动的同学补一下吧。

然后我们优化一下代码.只要你改变n的值就可以计算不同的值了。
int i ,sum = 0 ,n = 100;
sum = (1+n) * n /2;
return sum;
经过优化的代码是不是看起来就简单了许多,行数就少了许多。用最少的代码完成复杂的逻辑是一个码农的基本素养(狗头)。
讲了一大片乱七八糟的东西都还没引出算法的特性
输入、输出、有穷性、确定性、可行性这就是特性。最重要的是可行性和有穷性。不然你写个无限循环的代码出来,那就从入门到入牢了。
算法的效率
上面介绍了算法是个什么东西,还有基本特性。还进行了比较,但是呢比较还没有讲完。在数据结构当中,我们的计算机先驱给我们制定了一套验证算法效率的方法有事后检测法,事前检测法。
- 事后检测法:指的是通过检测算法在计算机中的运行时间来判断算法的效率。时间少,效率就高。这是一个方法,但是呢这个效率一定是正确的吗?难道以前的那种砖头机也能跑出10的评分吗?我的编译器不一样出来的还是相同的吗,答案是否定的。等算法运行完在看的效率很明显准确率不高。这啊那啊的影响。这就算是被我们遗弃了。
- 事前检测法:和上面相反,在算法还没运行时就开始进行检测。经过前人的分析我们一般进行以下步骤检测
2.1 算法采用的策略
2.2 编译产生代码的质量
2.3 问题输入的规模(就是输入)
2.4 执行代码的速度
这里主要讲述一下2.3吧。为什么呢?这里就不细讲了
求和
第一种
function a (n) {
let sum ; /*执行一次*/
for (let i = 0; i < n; i++) { /*执行n+1次*/
sum += i; /*执行n次*/
}
return sum; /*执行1次*/
}
第二种
int i ,sum = 0 ,n = 100; /*执行1次*/
sum = (1+n) * n /2; /*执行1次*/
return sum; /*执行1次*/
通过观察代码执行的次数,我们一眼就看出来那个算法更加优秀。还是前面的问题,你现在只运行100次没什么影响,到了一亿呢,一千万呢?那他要运行多少次呢?留给你自己想吧。
我们再看一段代码
function a (n) {
let sum ,j; /*执行一次*/
for (let i = 0; i <= n; i++) { /*执行n次*/
j++;
for (let k = 0; k < n; k++) {
sum += i; /*执行n次*/
}
}
return sum; /*执行1次*/
}
你再看看这两个内嵌循环。
当i=0时,里面的循环要走完i才到1,就相当于执行了n*n次。现在还没有问题等他到了指数的时候那就是爆炸函数了。这就是我们常说的大O表示法即算法的时间复杂度。
判断一个函数的时间复杂度,就是自己去走一遍代码,看看代码运行了几次(不用全部都走完,走出规律就行)。我们常见的就是有这几种时间复杂度
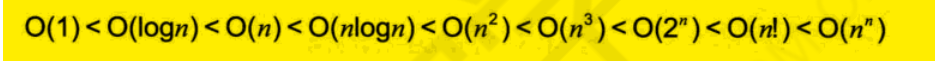
我们在判断的时候出现了什么n+1,2n+1这种。就可以直接不考虑常数了。直接要未知数就行。比如说n+1 n+20 都可以表示成O(n),因为常数的影响不大。详细的话那就要看书了。在看一例子吧

算法的最坏情况和最好情况
举个例子,以前的老人摔倒讹人的事件还有印象吧。小明出门的时候处于善良扶了老人起来没想到就被讹了十多万。那这不就是小明的最坏情况吗。最好的情况就是老人还嘉奖他了。对不对。我这里只是举个例子。没什么意思。回到算法,我们的求和从1加到100,是不是要加100次,如果我才加3次呢,那不是只运行3次吗?那他的O(n)还是这个吗?显然不是的。他就变成了O(1)【所有的常数都是写1】。还有一个平均的值。这里就不细说了。
空间复杂度
其实就是用空间换取时间。就是我用的内存加大,结果我都存进去了,你直接找就行。那不是方便快捷了吗?那你就要用钱了。给我死命加内存条。砸钱。