[数据结构与算法]动态规划问题集合（updating）

DP问题的特征

如果一个问题有在逐层向最优解进行一步一步地求解过程中，下一步有多种方案可以选择同时到达某一步可以从多个步骤求得，并且若是用广搜深搜技术难以实现或者时间复杂度超出所给限制时，我们可以考虑利用动态规划求解。

状态表示

首先动态规划需要用一个数组来表示某一状态，其中这一状态可分为集合和属性。

集合代表到达当前状态的所有情况的集合。
到达某一状态通常伴随着某种属性，这种属性可以是最大值、最小值和数量

递推方程

当前状态是由多个上一状态推导而来，则当前状态的属性从前一状态求得而来的方式就是递推方程

背包问题

01背包

有 $N$ 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 $v_i$，价值是 $w_i$。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价>值最大。
输出最大价值。

$$令f(i,j)的意义表示背包中物品个数没有超过i,体积没有超过j的所有方案的集合$$
$$令f(i,j)的属性表示当前状态下所有方案中的最大价值$$

则下来我们进行求递推方程的过程。

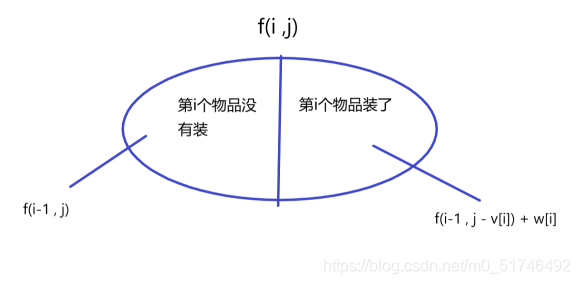
v代表体积，w代表价值
如图，当前状态（物品个数没有超过i,体积没有超过j）可以拿第i个物品到底有没有装进背包进行划分。如果第i个物品没有装进背包，则装的物品不超过$i?1$个时，其体积的最大值就有可能是就$j$，所以这一前一状态就是$f(i?1,j)$；如果第$i$个物品装进了背包，去除第$i$个物品时，装的物品不超过$i?1$，体积最大值不超过$j?v[i]$，此时再把物品$i$装进装进去，则这前一状态是$f(i?1,j?v[i])+w[i]$。所以由上述两种状态我们可知递推方程为：
$$f(i,j)=max(f(i?1,j),f(i?1,j?v_i)+w_i)$$

代码：

dp数组代表 f函数，vol是体积，val是价值
滚动数组优化稍后再写

#include <iostream>
using namespace std ;
const int N = 1005 ;
int dp[N][N] ;
int vol[N] , val[N] ;
int main(){
    int n , v ;
    
    cin >> n >> v;
    
    for(int i = 1 ; i <= n ; i ++){
        cin >> vol[i] >> val[i] ;
    }
    for(int i = 1 ; i <= n ; i ++){
        for(int j = 0 ; j <= v ; j ++){
            dp[i][j] = dp[i-1][j] ;
            if(j >= vol[i]) dp[i][j] = max(dp[i][j] , dp[i-1][j-vol[i]] + val[i]) ;
        }
    }
    
    cout << dp[n][v] << endl ;
    
    return 0 ;
}

更新中…