数据结构的定义:
1)数据是所有能被输入到计算机中,且能被计算机处理的符号的集合
2)数据是计算机操作的对象的总称,也是计算机处理的信息的某种特定的符号表示形式
(1)数据元素又被称为数据节点或者数据记录
是数据中的一个个体,数据的基本单位

(2)数据结构
带结构的数据元素的集合 (这里强调元素的集合,ID Status Type)
相互之间存在着某种特定关系的数据元素的集合(比如上面3113,3112两两相临就存在联系,线性关系)
数据以及数据元素相互之间的联系
(3)数据的存储结构
数据元素及其关系在计算机存储器中的存储方式,也称为数据的物理结构
比如说我想在计算机中存储 { ID Status Type}
可以实现为常用的Json类型 {"id":3113,"status":"Fixed","Type":"Gerrit"
"id":3112,"status":"Opened","Type":"Bugzilla"
}
定义好这种类型的数据结构就意味着要在计算机中分配存储空间用以保存数据,上图中显示给用户看的这个表格数据就是计算机已经
实现好的存储结构,是客观存在的数据结构所以也成为物理结构
(4)数据的运算
在上面存储结构的基础上可以进行一些增加修改和删除的操作
(5)数据结构的表示
该表中的记录顺序反映了数据元素之间的逻辑关系,为线性关系
用ID标识每条数据记录,数据间的逻辑关系表示为:<3111,3112>,<3112,3113>这样就确定了每条数据所在的位置
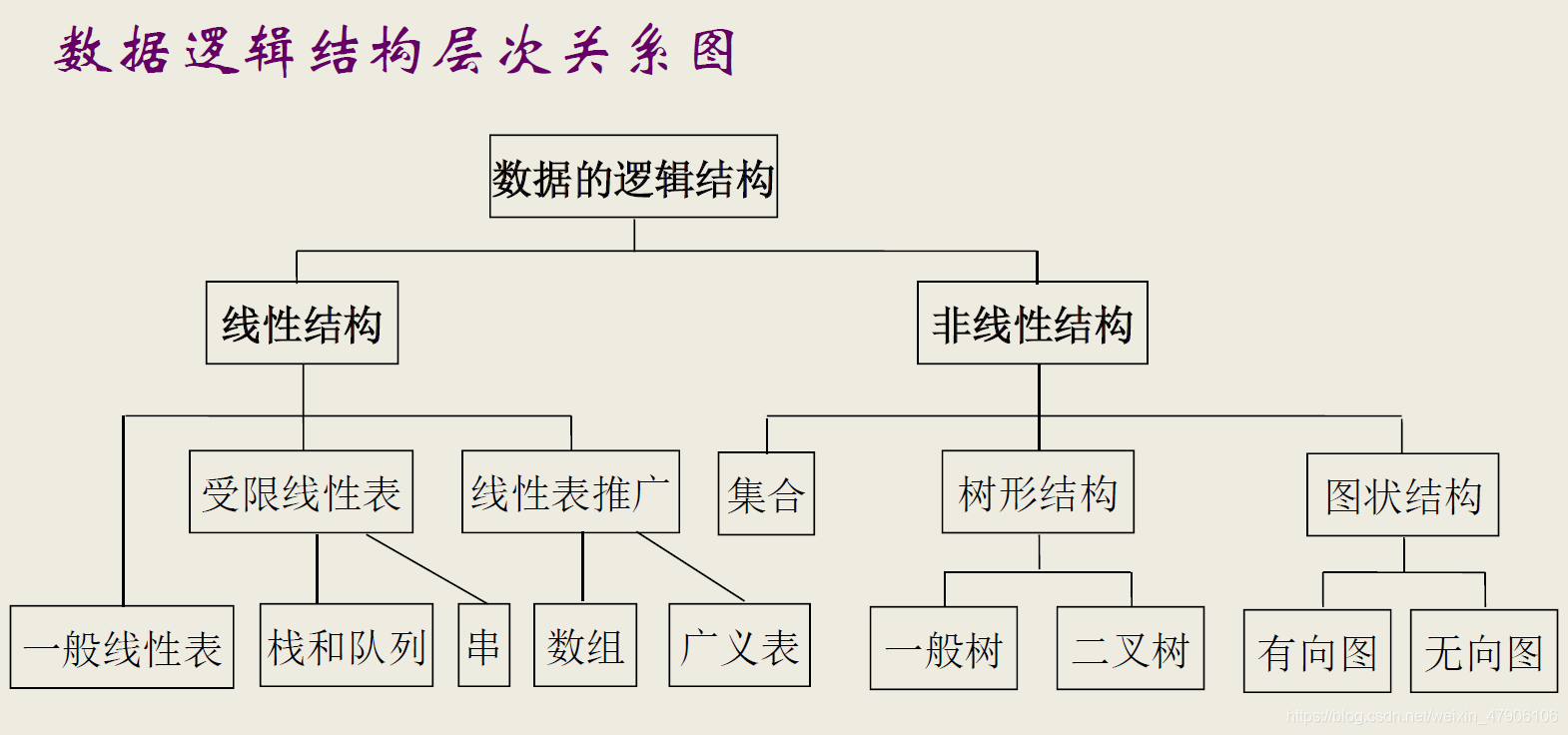
(6)逻辑结构类型
线性结构
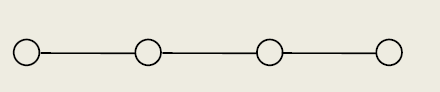
- 节点之间,一对一
- 开始节点和终端节点都是唯一的
- 除了开始节点和终端节点以外,其余节点都有且仅有一个前驱节点,有且仅有一个后继节点
树形结构,节点之间一对多
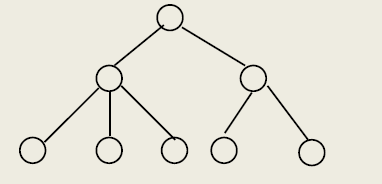
- 开始节点唯一,终端节点不唯一。
- 除终端节点以外,每个节点有一个或多个后续节点
- 除开始节点外,每个节点有且仅有一个前驱节点
图形结构,多对多
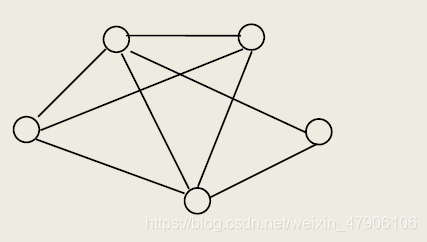
没有开始节点和终端节点,所有节点都可能有多个前驱节点和多个后继节点
算法及其描述
(1)算法的定义:算法是对特定问题求解方法(步骤)的一种描述,是指令的有限序列,其
中每一条指令表示一个或多个操作。
(2)算法的重要的特性
- 有穷性:在有穷步之后结束
- 可行性:可通过基本运算有限次执行来实现
- 有输入
- 有输出
(3)算法和程序的关系?
一个计算机程序是对一个算法使用某种程序设计语言的具体实现。算法必须可终止,意味着不是所有的计算机程序都是算法。
(4)算法复杂度
传统情况下效率的概念
- 单位时间完成的工作量
- 指最有效地使用社会资源以满足人类的愿望和需要
(5)算法的效率

有效地使用计算资源满足需求
- 时:用时短(CPU的计算资源)使用cpu在最短时间内完成运算
- 空:耗费的内存少(存储资源)尽可能占用少的内存空间,可以多用计算机跑几次算法
何为“用时短”的算法?
比如你这个算法是在超级计算机中运行的还是在普通计算机中运行的,这样不能叫用时短
所以:
- 不能用程序执行时间比较效率
- 执行的环境不同
- 实现的语言不同
- 其他因素
用基本运算的次数度量算法的时间复杂度
- 算法执行时间大致为基本运算所需的时间与其运算次数的乘积。
- 基本运算的一般是最深层循环内的语句
(6)算法的时间复杂度
原理:在一个算法中,进行基本运算的次数越少,其运行时间也就相对地越少;基本运算次数越多,,其运行时间也就相对地越多。
定义:把算法中包含基本运算次数的多少称为算法的时间复杂度,也就是说,一个算法的时间复杂度是指该算法的基本运算次数。
度量:算法中基本运算次数T(n)是问题规模n的某个函数f(n),记作:T(n)=O(f(n))
“大O”
- 表示时间复杂度的“量级”
- 随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同。
比如:T(n)=5n2-2n+10000=O(n2)
- 只关注T(n)的最高阶,忽略其低阶项和常系数,这样既可简化T(n)的计算,又能比较客观地反映出当n很大时算法的时间性能。
- 算法分析只关心n很大时的表现。
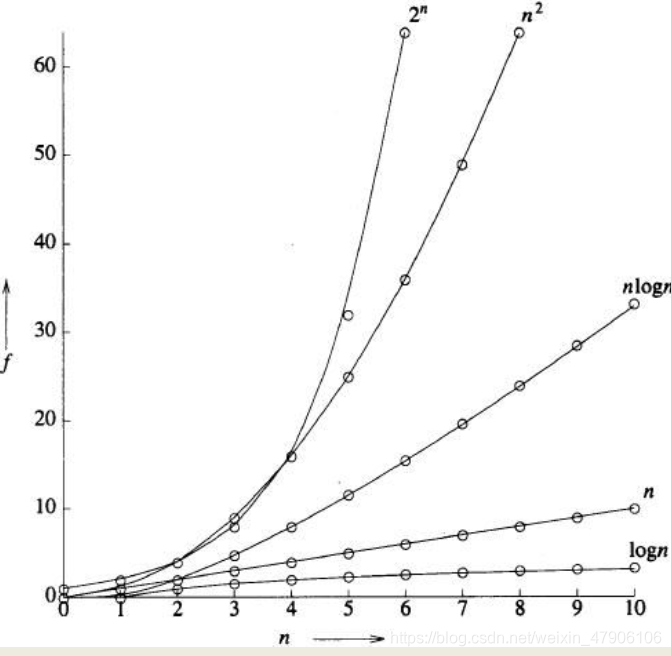
(7)复杂度的量级
- O(1),常数阶 复杂度与问题规模n无关 比如:没有循环的算法
- O(log2n),对数阶 同 O(lgn), O(lbn)
- O(n),线性阶 与问题规模n的增长呈线性增大关系, 比如:有执行n次的一重循环的算法
- O(nlog2n) 线性对数阶
- O(n2),平方阶 多项式阶算法为有效算法。
- O(n3),立方阶 多项式阶算法为有效算法。
- O(2n),指数阶
O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2n)<O(n!)