题目大意:
有一个初始序列,你要维护其3个操作:
1.格式:1 x y k 表示把区间[x,y]乘以k。
2.格式:2 x y k 表示把区间[x,y]加上k。
3.格式:3 x y 表示求区间[x,y]的和。
思路:
标准的线段树模板,蒟蒻打了3小时才过。
解题过程:
线段树是一种灵活的数据结构,在信竞中较为常见。
它的原理是这样的:
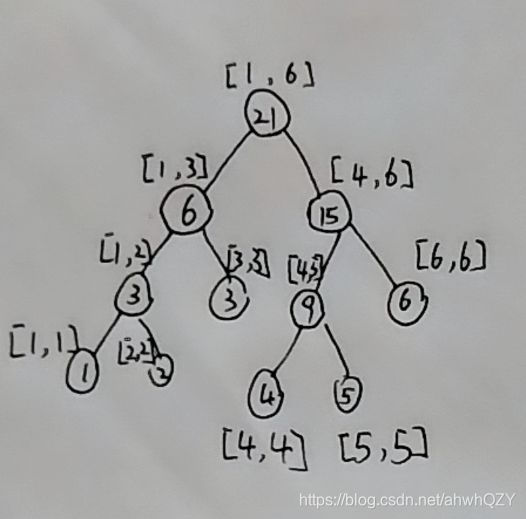
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?上图为区间[1,6]的线段树
?序列中的每个元素即为线段树中的叶子节点,在一个子树中父节点=左孩子+右孩子。
所以定义一个结构体:
struct Node{
ll l,r,k;//左孩子,右孩子,值
ll add,mul;//加法和乘法
}tree[N<<2];//N<<2=N*4,线段树空间通常开4倍大那我们如何建树呢?
上文说了,当节点为孩子节点是便是序列值,所以l==r时就是叶子节点。
所以建树程序如下:
inline ll build_tree(ll value,ll l,ll r){//ll 为提前定义的long long
tree[value]=Node{l,r,0,0,1};//初始化
if (l==r){
ll num;
scanf("%lld",&num);
return tree[value].k=num%Mod;//存储时注意取模
}
ll mid=(l+r)>>1;
return tree[value].k=(build_tree(value<<1,l,mid)+build_tree(value<<1|1,mid+1,r))%Mod;
//线段树左边加右边
}接着就是更新节点环节了,要更新3部分:
加法更新,乘法更新,和的更新。
inline void pushdown(ll value){
tree[value*2].add=(tree[value].add+tree[value*2].add*tree[value].mul)%Mod;
//左孩子加法更新:不用担心tree[value].mul没有值,初始化时变成1的
tree[value*2+1].add=(tree[value].add+tree[value*2+1].add*tree[value].mul)%Mod;
//右孩子加法更新,同上
tree[value*2].mul=(tree[value].mul*tree[value*2].mul)%Mod;
tree[value*2+1].mul=(tree[value].mul*tree[value*2+1].mul)%Mod;
//乘法更新时不会乘上加法,注意!
tree[value*2].k=(tree[value].mul*tree[value*2].k+tree[value].add*(tree[value*2].r-tree[value*2].l+1))%Mod;
tree[value*2+1].k=(tree[value].mul*tree[value*2+1].k+tree[value].add*(tree[value*2+1].r-tree[value*2+1].l+1))%Mod;
//更新左右孩子当前值
tree[value].add=0;
tree[value].mul=1;
//还原
}我们还有要区间更新的地方updata,见下:
inline void updata(ll value,ll x,ll pos,ll L,ll R){
pushdown(value);//单点修改
if (pos==1&&tree[value].l>=L&&tree[value].r<=R){//乘法操作
tree[value].mul=(tree[value].mul*x)%Mod;
tree[value].add=(tree[value].add*x)%Mod;
tree[value].k=(tree[value].k*tree[value].mul)%Mod;
return;
}
if(pos==2&&tree[value].l>=L&&tree[value].r<=R){//加法操作
tree[value].add=(tree[value].add+x)%Mod;
tree[value].k=(tree[value].k+tree[value].add*(tree[value].r-tree[value].l+1))%Mod;
return;
}
ll mid=(tree[value].l+tree[value].r)/2;//分为2个区间
if(L<=mid)
updata(value*2,x,pos,L,R);
if(R>mid)
updata((value*2)+1,x,pos,L,R);
tree[value].k=(tree[value*2].k+tree[value*2+1].k)%Mod;//tree[value].k的更新直接两边相加
}那这时候只缺查询操作了。
inline ll query(ll value,ll L,ll R){
pushdown(value);//单点修改
if (tree[value].l>=L&&tree[value].r<=R)
return tree[value].k%Mod;//如果是已经合并了的,直接返回
ll mid=(tree[value].l+tree[value].r)>>1;
return ((L<=mid?query(value*2,L,R):0)+(R>mid?query(value*2+1,L,R):0))%Mod;
//左区间如果存在就加,右区间同理
}至此,我们的线段树终于完成。
下面贴出此题代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+1;
struct Node{
ll l;
ll r;
ll k;
ll add;
ll mul;
}tree[N*4];
ll n,m,Mod,pos;
inline ll build_tree(ll value,ll l,ll r){
tree[value]=Node{l,r,0,0,1};
if (l==r){
ll num;
scanf("%lld",&num);
return tree[value].k=num%Mod;
}
ll mid=(l+r)>>1;
return tree[value].k=(build_tree(value*2,l,mid)+build_tree(value*2+1,mid+1,r))%Mod;
}
inline void pushdown(ll value){
tree[value*2].add=(tree[value].add+tree[value*2].add*tree[value].mul)%Mod;
tree[value*2+1].add=(tree[value].add+tree[value*2+1].add*tree[value].mul)%Mod;
tree[value*2].mul=(tree[value].mul*tree[value*2].mul)%Mod;
tree[value*2+1].mul=(tree[value].mul*tree[value*2+1].mul)%Mod;
tree[value*2].k=(tree[value].mul*tree[value*2].k+tree[value].add*(tree[value*2].r-tree[value*2].l+1))%Mod;
tree[value*2+1].k=(tree[value].mul*tree[value*2+1].k+tree[value].add*(tree[value*2+1].r-tree[value*2+1].l+1))%Mod;
tree[value].add=0;
tree[value].mul=1;
}
inline ll query(ll value,ll L,ll R){
pushdown(value);
if (tree[value].l>=L&&tree[value].r<=R)
return tree[value].k%Mod;
ll mid=(tree[value].l+tree[value].r)>>1;
return ((L<=mid?query(value*2,L,R):0)+(R>mid?query(value*2+1,L,R):0))%Mod;
}
inline void updata(ll value,ll x,ll pos,ll L,ll R){
pushdown(value);
if (pos==1&&tree[value].l>=L&&tree[value].r<=R){
tree[value].mul=(tree[value].mul*x)%Mod;
tree[value].add=(tree[value].add*x)%Mod;
tree[value].k=(tree[value].k*tree[value].mul)%Mod;
return;
}
if(pos==2&&tree[value].l>=L&&tree[value].r<=R){
tree[value].add=(tree[value].add+x)%Mod;
tree[value].k=(tree[value].k+tree[value].add*(tree[value].r-tree[value].l+1))%Mod;
return;
}
ll mid=(tree[value].l+tree[value].r)/2;
if(L<=mid)
updata(value*2,x,pos,L,R);
if(R>mid)
updata((value*2)+1,x,pos,L,R);
tree[value].k=(tree[value*2].k+tree[value*2+1].k)%Mod;
}
int main(){
scanf("%lld%lld",&n,&Mod);
build_tree(1,1,n);
cin>>m;
for (ll i=1;i<=m;i++){
cin>>pos;
ll x,y;
cin>>x>>y;
if (pos!=3){
ll k;
cin>>k;
updata(1,k,pos,x,y);
}
else if (pos==3)
printf("%lld\n",query(1,x,y));
}
}