[数据结构与算法]栈与队列--Java

栈(Stack)与队列(Queue)

栈

定义:

一种运算受限的线性数据结构,只能在表尾进行插入删除操作(栈底固定,栈顶浮动),表尾称为栈顶,另一端称为栈底

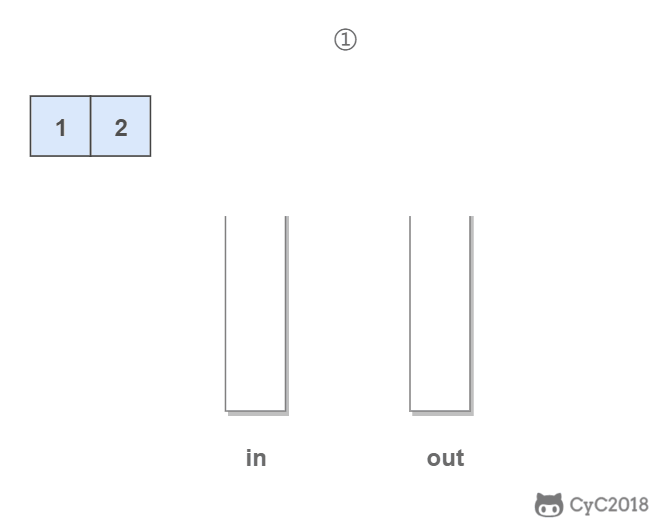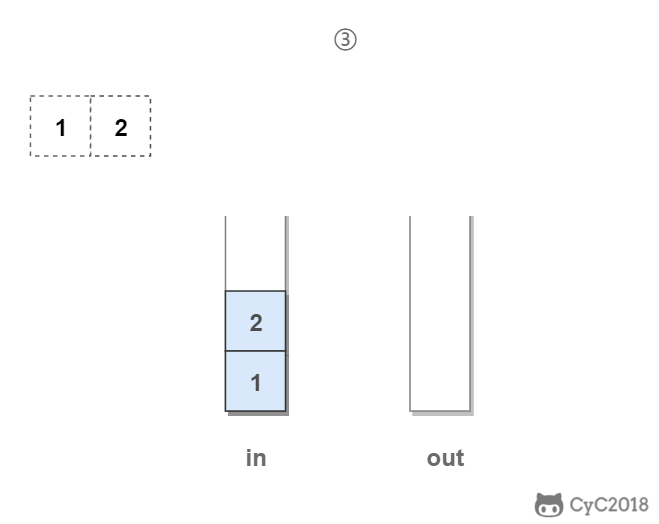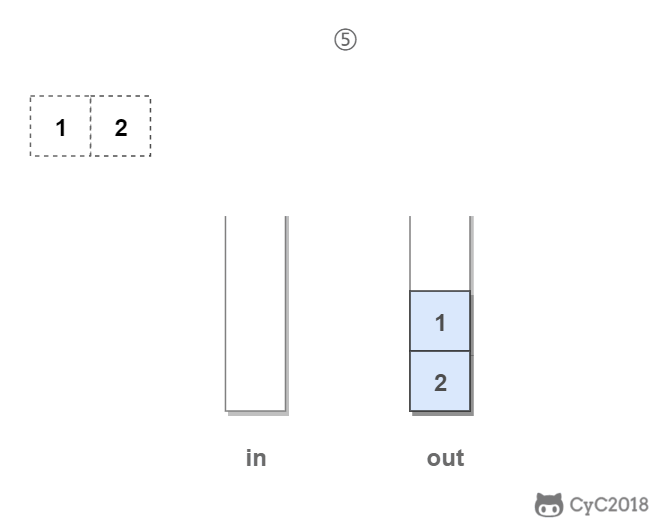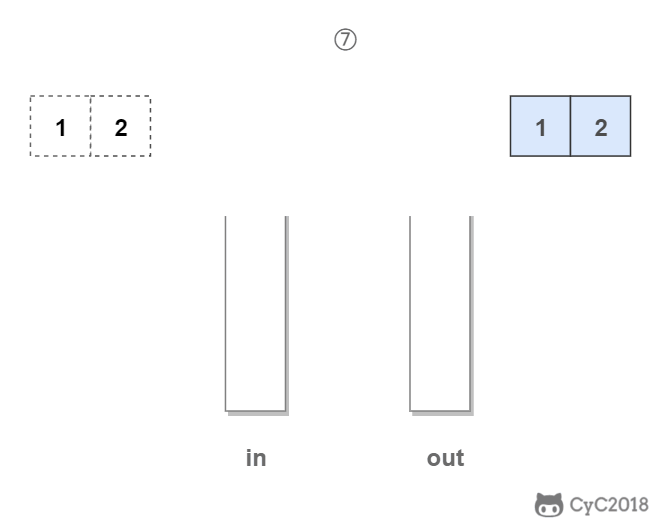
特点:

• 后进先出
• Last In First Out(LIFO)

操作:

• push(E) 入栈
• pop() 出栈
• peek() 返回栈顶元素
• getSize() 返回栈中元素个数
• isEmpty() 判断栈是否为空

栈的实现

创建一个stack接口,声明栈的几个基本方法

public interface Stack<T> {

    /**
     * 压栈
     * @param elem
     */
    void push(T elem);

    /**
     * 弹栈
     * @return
     */
    T pop();

    /**
     * 查看栈顶元素
     * @return
     */
    T peek();

    /**
     * 返回栈中元素个数
     * @return
     */
    int getSize();

    /**
     * 判断栈是否为空
     * @return
     */
    boolean isEmpty();
}

数组实现

使用之前的自定义数组类来实现自定义栈

package com.company.project.subject.day2.stack;

/**
 * 数组
 */
public class MyselfArray<T> {

    //数组当前元素个数
    private int size;

    //数组
    private T[] data;

    /**
     * 默认无参构造容量为10的数组
     */
    public MyselfArray() {
        this(10);
    }

    /**
     * 有参构造方法
     *
     * @param capacity 数组可存的容量
     */
    public MyselfArray(int capacity) {
        this.size = 0;
        data = (T[]) new Object[capacity];//强制类型转换
    }

    /**
     * 向指定位置添加元素
     *
     * @param index 索引
     */
    public void add(int index, T elem) {
        //目标索引必须处在0~size之间
        if (index < 0 || index > this.size) {
            throw new IllegalArgumentException("index is error");
        }

        //当数组容量已满时,进行扩容操作(2倍)
        if (this.size == data.length) {
            resize(2 * data.length);
        }

        /*
            将要插入的元素后方向后移
            1.从后向前遍历,找到插入位置(0~size)
            2.将插入位置之后的所有元素全部向后移一位
            3.插入一个元素后,size+1
         */
        //          末尾元素   到要插入的下标停止遍历
        for (int i = this.size - 1; i >= index; i--) {
            //将目标索引及之后的元素向后移
            data[i + 1] = data[i];
        }
        //将目标元素添加到目标位置
        data[index] = elem;
        //添加元素后,有效元素数+1
        this.size++;
        //释放空间
        //data[size]=null;

    }

    /**
     * 向头部添加元素
     */
    public void addFirst(T elem) {
        //头部索引为0
        add(0, elem);
    }

    /**
     * 向末尾添加元素
     */
    public void addLast(T elem) {
        //尾部待插入元素索引为size
        //index : 0 1 2 3 4 5 
        //size  : 1 2 3 4 5 null  
        add(this.size, elem);
    }

    /**
     * 重新设置容量大小,进行扩容/缩容
     *
     * @param newCapacity 新数组容量
     */
    public void resize(int newCapacity) {
        //创建新数组
        T[] newData = (T[]) new Object[newCapacity];
        //复制元素
        for (int i = 0; i < this.size; i++) {
            newData[i] = data[i];
        }
        //复制数组
        this.data = newData;
    }

    /**
     * 删除指定位置的元素
     *
     * @param index 目标索引
     * @return 目标索引的值
     */
    public T remove(int index) {
        //目标索引必须处在0~size-1之间
        if (index < 0 || index >= this.size) {
            throw new IllegalArgumentException("index is invalid");
        }

        //当有效元素数<=数组容量的1/4时    缩容 为 1/2
        if (this.size <= (data.length / 4) && data.length / 2 > 0) {
            resize(data.length / 2);
        }

        //记录将被删除的元素
        T result = data[index];

        /*
            将要插入的元素后方向后移
            1.从前向后遍历,找到删除位置(0~size-1)
            2.记录待删除位置的元素
            2.将删除位置之后的所有元素全部向前移一位
            3.删除一个元素后,size-1
         */

        //将目标索引之后的索引对应元素向前移一位
        for (int i = index + 1; i < this.size; i++) {
            data[i - 1] = data[i];
        }

        this.size--;
        data[size] = null;

        //返回被删除的元素
        return result;

    }

    /**
     * 删除指定的元素
     * (若有重复元素  只能删除第一次找到的元素)
     *
     * @param elem 目标元素
     * @return 目标元素的索引
     */
    public int removeElem(T elem) {
        int index = this.isContains(elem);

        if (index == -1) {
            return -1;
        } else {
            remove(index);
        }

        return index;
    }

    /**
     * 删除第一个元素
     */
    public T removeFirst() {
        return remove(0);
    }

    /**
     * 删除末尾元素
     */
    public T removeLast() {
        return remove(this.size - 1);
    }


    /**
     * 返回指定位置的元素
     *
     * @param index 返回数组元素的索引
     * @return int
     */
    public T getElemByIndex(int index) {
        //当索引不在有效元素范围内(0~size-1)时
        if (index < 0 || index >= this.size) {
            throw new ArrayIndexOutOfBoundsException("index is error");
        }

        return data[index];
    }

    /**
     * 修改指定位置的元素
     *
     * @param index
     * @param elem
     */
    public void modifyElemByIndex(int index, T elem) {
        //当索引不在有效元素范围内(0~size-1)时
        if (index < 0 || index >= this.size) {
            throw new ArrayIndexOutOfBoundsException("index is error");
        }

        data[index] = elem;
    }

    /**
     * 判断数组是否为空
     *
     * @return boolean
     */
    public boolean isEmpty() {
        return this.size == 0;
    }


    /**
     * 是否包含指定的元素
     *
     * @param elem 目标元素
     * @return int
     */
    public int isContains(T elem) {
        for (int i = 0; i < size; i++) {
            //包含返回目标元素索引
            if (data[i].equals(elem)) {
                return i;
            }
        }

        //不包含返回-1
        return -1;
    }

    /**
     * 重写toString
     *
     * @return String
     */
    @Override
    public String toString() {
        StringBuffer stringBuffer = new StringBuffer();
        stringBuffer.append("[");

        for (int i = 0; i < this.size; i++) {
            stringBuffer.append(data[i]);
            //每个元素用","隔开
            if (i != this.size - 1) {
                stringBuffer.append(",");
            }
        }

        stringBuffer.append("]");
        return stringBuffer.toString();
    }

    /**
     * 返回元素个数
     *
     * @return int
     */
    public int getSize() {
        return this.size;
    }

    /**
     * 返回数组容量
     *
     * @return int
     */
    public int getCapacity() {
        return data.length;
    }

    /**
     * 返回最后一个元素
     * @return
     */
    public T getLastElem(){
        return data[size-1];
    }

    /**
     * 返回第一个元素
     * @return
     */
    public T getFirstElem(){
        return data[0];
    }

}

自定义栈

package com.company.project.subject.day2.stack;

public class MyStack<T> implements Stack<T>{

    /**
     * 使用数组实现栈
     */
    MyselfArray<T> myArray;

    /**
     * 构造方法
     */
    public MyStack(){
        this(10);
    }

    public MyStack(int capacity){
        myArray=new MyselfArray<T>(capacity);
    }


    /**
     * 压栈
     * @param elem
     */
    @Override
    public void push(T elem) {
        myArray.addLast(elem);
    }

    /**
     * 弹栈
     * @return
     */
    @Override
    public T pop() {
        //删除末端元素,并返回
        return myArray.removeLast();
    }

    /**
     * 返回栈顶元素
     * @return
     */
    @Override
    public T peek() {
        return myArray.getLastElem();
    }

    /**
     * 返回有效元素个数
     * @return
     */
    @Override
    public int getSize() {
        return myArray.getSize();
    }

    /**
     * 判断栈是否为空
     * @return
     */
    @Override
    public boolean isEmpty() {
        return myArray.isEmpty();
    }

    @Override
    public String toString() {
        StringBuilder stringBuilder = new StringBuilder();

        stringBuilder.append("栈元素数: "+this.getSize()+"  栈容量: "+myArray.getCapacity()+"  栈元素:\r\n");
        while (!this.isEmpty()){
            stringBuilder.append(this.pop()+"<<<");
        }
        return stringBuilder.substring(0,stringBuilder.lastIndexOf("<")-2).toString();
    }
}

测试

package com.company.project.subject.day2.stack;

public class StatckTest {
    public static void main(String[] args) {

        Stack<Integer> stack = new MyStack<>();

        System.out.println("当前栈为空:"+stack.isEmpty());

        for (int i = 0; i < 5; i++) {
            stack.push(i);
        }
        
        System.out.println(stack.toString());
    }
}

运行:

package com.company.project.subject.day2.stack;

public class StatckTest {
    public static void main(String[] args) {

        Stack<Integer> stack = new MyStack<>();

        System.out.println("当前栈为空:"+stack.isEmpty());

        for (int i = 0; i < 5; i++) {
            stack.push(i);
        }
        
        //System.out.println(stack.toString());


        System.out.println("栈当前元素个数:"+stack.getSize());

        int length = stack.getSize();
        /**
         * 遍历栈时若使用getSize() 当弹栈时,元素个数发生变化,应将栈的元素个数取出
         */
        for (int i = 0; i<length; i++) {
            System.out.print(stack.pop());
        }

    }
}

运行:

链表实现

先空着…

栈的应用

有效的括号(20)

链接：https://leetcode-cn.com/problems/valid-parentheses

题目:

给定一个只包括 ‘(’，’)’，’{’，’}’，’[’，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

 /**
     * 第20题 有效的括号
     * 1.判断栈是否为空
     * 2.将左(右)括号压栈
     * 3.将右(左)括号与栈中的括号弹出相比较
     * 4.直到栈为空返回true
     * @param s
     * @return
     */
    public boolean isValid(String s) {

        Stack<Character> stringStack = new Stack();

        //判断参数是否合法
        if (s==null){
            throw new IllegalArgumentException("字符串为空");
        }

        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            //将左括号压栈
            if(ch=='{'||ch=='('||ch=='['){
                stringStack.push(ch);
            }else{
                //判断当前栈是否为空
                if(stringStack.isEmpty()){
                    return false;
                }
                //弹出左括号
                char res = stringStack.pop();
                //比较左括号与右括号
                if(res=='{'&&ch!='}'){
                    return false;
                }
                if(res=='['&&ch!=']'){
                    return false;
                }
                if(res=='('&&ch!=')'){
                    return false;
                }
            }
        }

        //遍历完后若栈为空,则返回true
        return stringStack.isEmpty();
    }

棒球比赛(682)

比赛开始时，记录是空白的。你会得到一个记录操作的字符串列表 ops，其中 ops[i] 是你需要记录的第 i 项操作，ops 遵循下述规则：

整数 x - 表示本回合新获得分数 x
“+” - 表示本回合新获得的得分是前两次得分的总和。题目数据保证记录此操作时前面总是存在两个有效的分数。
“D” - 表示本回合新获得的得分是前一次得分的两倍。题目数据保证记录此操作时前面总是存在一个有效的分数。
“C” - 表示前一次得分无效，将其从记录中移除。题目数据保证记录此操作时前面总是存在一个有效的分数。
请你返回记录中所有得分的总和。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/baseball-game

package com.company.project.arithmetic;
import java.util.Stack;

/**
 *  棒球比赛
 */
public class Solution682 {

    public static void main(String[] args) {
        String[] ops = {"5","2","C","D","+"};
        System.out.println(new Solution682().calPoints(ops));
    }

    /**
     *
     * @param ops 操作序列
     * @return 总分
     */
    public int calPoints(String[] ops) {
        int res = 0;//记录总分

        if (ops == null) {
            throw new IllegalArgumentException("所给记录为空!");
        }

        Stack<Integer> scoreStack = new Stack();

        for (int i = 0; i < ops.length; i++) {
            String s = ops[i];
            switch (s) {
                case "C":
                    //清除前一次分数,并保证每次操作前面存在分数
                    if (scoreStack.size() < 1) {
                        throw new IllegalArgumentException("数据不合法");
                    }
                    scoreStack.pop();//出栈
                    break;
                case "D":
                    //本次得分为前一次记录的2倍
                    if (scoreStack.size() < 1) {
                        throw new IllegalArgumentException("数据不合法");
                    }
                    scoreStack.push(scoreStack.peek() * 2);
                    break;
                case "+":
                    //本次得分为前两次记录之和
                    if(scoreStack.size()<2){
                        throw new IllegalArgumentException("数据不合法");
                    }
                    int scoreTemp1 = scoreStack.pop();//前一次得分
                    int scoreTemp2 = scoreTemp1 + scoreStack.peek();//本次得分
                    scoreStack.push(scoreTemp1);//将前一次得分入栈
                    scoreStack.push(scoreTemp2);//将本次得分入栈
                    break;
                default:
                    //将分数入栈
                    scoreStack.push(Integer.parseInt(s));
                    break;
            }
        }
        //求栈中分数总和
        while (!scoreStack.isEmpty()) {
            res += scoreStack.pop();
        }
        return res;
    }
}

1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

输入："abbaca"
输出："ca"

package com.company.project.arithmetic.leetcode;
import java.util.Stack;
public class Solution1047 {
    public String removeDuplicates(String s) {
        Stack<String> stack = new Stack<>();
        for (int i = 0; i < s.length(); i++) {
            //取出字符串中的单个字符
            String s1 = String.valueOf(s.charAt(i));
            //栈空时入栈
            if(stack.isEmpty()){
                stack.push(s1);
            }else if(stack.peek().equals(s1)){
                //栈顶元素与即将入栈元素相同,出栈
                stack.pop();
            }else {
                stack.push(s1);
            }
        }

        StringBuilder res = new StringBuilder();
        for(String ss: stack){
            res.append(ss);
        }

        return res.toString();
    }

    public static void main(String[] args) {
        System.out.println(new Solution1047().removeDuplicates("abbaca"));
    }
}

队列

定义:

队列是一种操作受限的先线性表,只能在队首(即表头)front进行删除,队尾(即表尾)tail进行插入操作

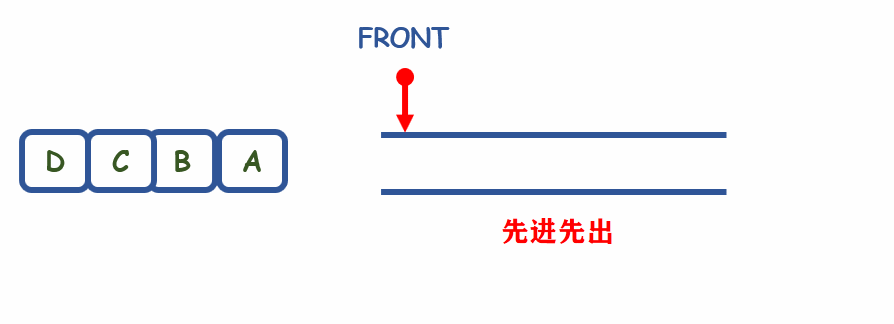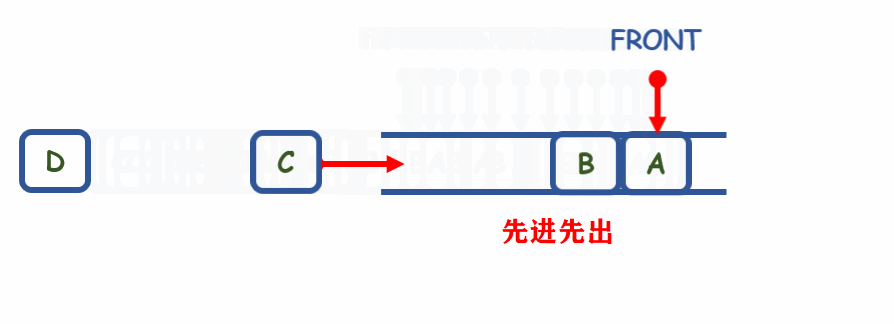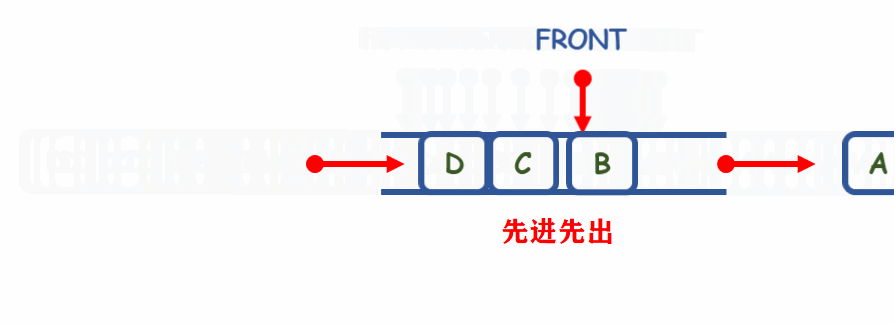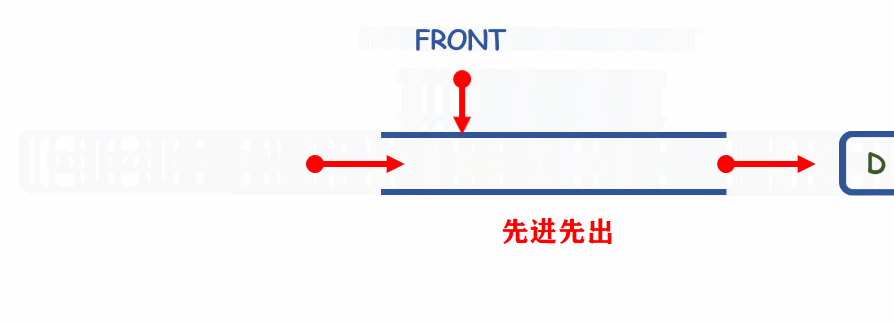
特点:

• 先进先出
• First In First Out(FIFO)

操作

• enqueue(E e) 入队
• dequeue() 出队
• getFront() 返回队首元素
• getSize() 返回队列元素个数
• isEmpty() 判断队列是否为空

队列的实现

数组队列

声明一个队列接口

package com.company.project.subject.day2.queue;

public interface Queue<T> {

    //入队
    void enqueue(T elem);

    //出队
    T dequeue();

    //返回队首元素
    T getFront();

    //返回有效元素数
    int getSize();

    //判断是否为空
    boolean isEmpty();
    
}

使用数组实现

package com.company.project.subject.day2.queue;
import com.company.project.subject.day2.stack.MyselfArray;
public class MyQueue<T> implements Queue<T> {

    private MyselfArray<T> myArray;

    /**
     * 无参构造方法
     */
    public MyQueue(){
        this(10);
    }

    /**
     * 有参构造
     * @param capacity 初始化队列容量
     */
    public MyQueue(int capacity){
        myArray=new MyselfArray<>(capacity);
    }

    /**
     * 入队
     * @param elem 入队元素
     */
    @Override
    public void enqueue(T elem) {
        myArray.addLast(elem);
    }

    /**
     * 出队
     * @return 队首元素
     */
    @Override
    public T dequeue() {
        return myArray.removeFirst();
    }

    /**
     * 返回队首元素
     * @return 队首元素
     */
    @Override
    public T getFront() {
        return myArray.getFirstElem();
    }

    /**
     * 返回队列中有效元素数
     * @return 有效元素数
     */
    @Override
    public int getSize() {
        return myArray.getSize();
    }

    /**
     * 判断队列是否为空
     * @return boolean
     */
    @Override
    public boolean isEmpty() {
        return myArray.isEmpty();
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();

        if(this.isEmpty()){
            return null;
        }

        sb.append("队首>>> ");
        while (!this.isEmpty()){
            sb.append(this.dequeue()+",");
        }
        String str= sb.substring(0, sb.lastIndexOf(","));

        str+=" <<<队尾";

        return str.toString();
    }
}

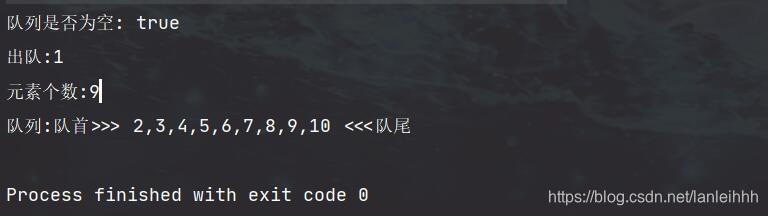
测试

package com.company.project.subject.day2.queue;
import com.company.project.subject.day2.queue.MyQueue;
public class QueueTest {

    public static void main(String[] args) {

        MyQueue<Integer> myQueue = new MyQueue<>();
        System.out.println("队列是否为空: "+myQueue.isEmpty());

        for (int i = 0; i < 10; i++) {
            myQueue.enqueue(i+1);
        }
        System.out.println("出队:"+myQueue.dequeue());
        System.out.println("元素个数:"+myQueue.getSize());
        System.out.println("队列:"+myQueue);

    }
}

时间复杂度分析

• enqueue(E e) O(1)
• dequeue() O(n) 出队后还要将其他元素前移
• getFront() O(1)
• getSize() O(1)
• isEmpty() O(1)

循环队列

使用数组实现队列的问题

在进行出队操作时,出队队首元素,其余元素需前移,时间复杂度为O(N)

为了解决每次出队需要移动其余数组元素的问题,我们使用front来记录队首的位置,tail记录队尾

• 情况1

  • front==tail 队列为空

  

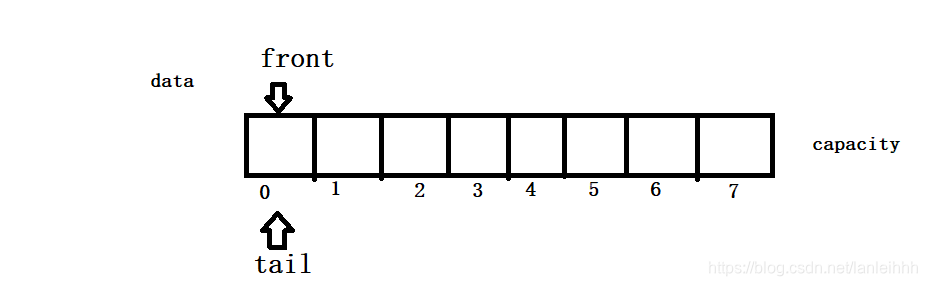
• 情况2

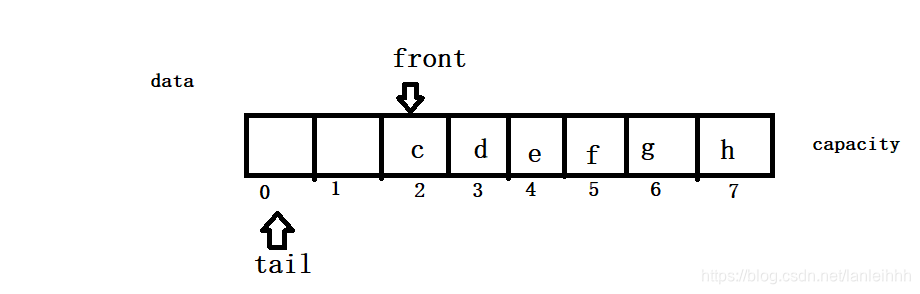
• 情况3 (tail+1)%capacity==front 队满

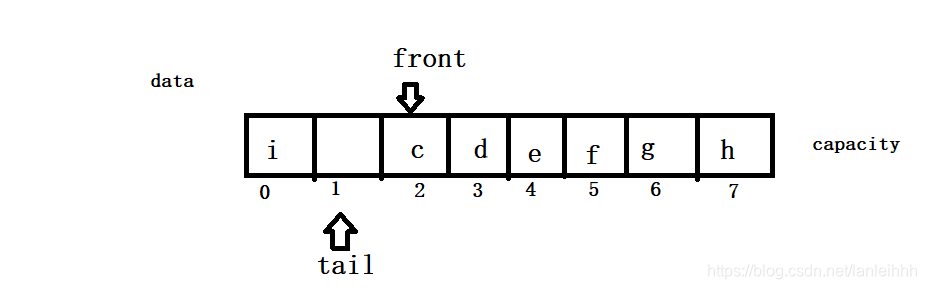
实现循环队列

新建一个自己的循环队列类

package com.company.project.subject.day2.queue;
public class LoopQueue<T> {
}

声明属性

	//数据容器
    private T[] data;
    //有效元素个数
    private int size;
    //队首指针
    private int frant;
    //队尾指针
    private int tail;

构造方法

	public LoopQueue() {
        this(10);
    }

    public LoopQueue(int capacity) {
    	//初始化时多创建一个多余空间
        data = (T[]) new Object[capacity+1];
        this.size = 0;
        this.frant = 0;
        this.tail = 0;
    }

返回队首元素

public T getFront() {
        //队列不为空返回队首元素
        if (this.isEmpty()) {
            throw new IllegalArgumentException("this queue is empty");
        }
        return data[this.frant];
    }

改变容量

public void resize(int newCapacity) {
        //创建一个新的泛型数组
        T[] newDate = (T[]) new Object[newCapacity];

        //遍历原数组,将原数组的值赋值到新数组中
        for (int i = 0; i < this.size; i++) {
            newDate[i] = data[(this.frant + i) % getCapacity()];
        }
		
        //用新数组替换原数组
        this.data = newDate;
        //队首指针指向0索引
        this.frant = 0;
		//队尾指针指向队尾元素的下一个元素
        this.tail = this.size;
    }

入队

	//入队
    public void enQueue(T elem) {
        //判断队列是否已满
        if ((tail + 1) % this.getCapacity() == this.frant) {
            //扩容         预留一个不用的空间
            resize(this.getCapacity() * 2 - 1);
        }

        this.data[this.tail] = elem;
        this.size++;
        //尾指针向后移
        this.tail = (this.tail + 1) % this.getCapacity();
    }

出队

	//出队
    public T deQueue() {
        if (this.isEmpty()) {
            throw new IllegalArgumentException("this queue is empty");
        }

        //记录队首元素
        T res = this.data[this.frant];
        //有效元素数-1
        this.size--;
        //首指针向后移
        this.frant = (this.frant + 1) % this.getCapacity();

        //当前队列元素个数等于总容量的1/4,且总容量>3时 缩容
        if ((this.getSize() == this.getCapacity() / 4) && (this.getCapacity() / 2 > 1)) {
            //预留一个不用的空间
            resize((this.getCapacity() + 1) / 2);
        }

        return res;//返回队首元素
    }

其他方法

	//判断循环队列是否为空
    public boolean isEmpty() {
        return this.frant == this.tail;
    }

    //获取循环队列的有效元素个数
    public int getSize() {
        return this.size;
    }

    //获取循环队列的容量
    public int getCapacity() {
        return data.length;
    }

	//重写toString()
	@Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        if(this.isEmpty()){
            return null;
        }
        sb.append("队首>>> ");
        while (!this.isEmpty()){
            sb.append(this.deQueue()+",");
        }
        String str= sb.substring(0, sb.lastIndexOf(","));
        str+=" <<<队尾";
        
        return str.toString();
    }

完整代码

package com.company.project.subject.day2.queue;
public class LoopQueue<T> {

    //数据容器
    private T[] data;
    //有效元素个数
    private int size;
    //队首指针
    private int frant;
    //队尾指针
    private int tail;

    public LoopQueue() {
        this(10);
    }

    public LoopQueue(int capacity) {
        data = (T[]) new Object[capacity];
        this.size = 0;
        this.frant = 0;
        this.tail = 0;
    }

    //判断循环队列是否为空
    public boolean isEmpty() {
        return this.frant == this.tail;
    }

    //获取循环队列的有效元素个数
    public int getSize() {
        return this.size;
    }

    //获取循环队列的容量
    public int getCapacity() {
        return data.length;
    }

    //返回循环队列的队首元素
    public T getFront() {
        //队列不为空返回队首元素
        if (this.isEmpty()) {
            throw new IllegalArgumentException("this queue is empty");
        }
        return data[this.frant];
    }

    //入队
    public void enQueue(T elem) {
        //判断队列是否已满
        if ((tail + 1) % this.getCapacity() == this.frant) {
            //扩容         预留一个不用的空间
            resize(this.getCapacity() * 2 - 1);
        }

        this.data[this.tail] = elem;
        this.size++;
        //尾指针向后移
        this.tail = (this.tail + 1) % this.getCapacity();
    }

    /**
     * 扩容/缩容
     *
     * @param newCapacity
     */
    public void resize(int newCapacity) {
        //创建一个新的泛型数组
        T[] newDate = (T[]) new Object[newCapacity];

        //遍历原数组,将原数组的值赋值到新数组中
        for (int i = 0; i < this.size; i++) {
            newDate[i] = data[(this.frant + i) % getCapacity()];
        }

        //用新数组代替原数组
        this.data = newDate;
        //首指针指向0
        this.frant = 0;

        this.tail = this.size;
    }

    //出队
    public T deQueue() {
        if (this.isEmpty()) {
            throw new IllegalArgumentException("this queue is empty");
        }

        //记录队首元素
        T res = this.data[this.frant];
        //有效元素数-1
        this.size--;
        //首指针向后移
        this.frant = (this.frant + 1) % this.getCapacity();

        //当前队列元素个数小于等于总容量的1/4,且总容量>3时 缩容
        if ((this.getSize() <= this.getCapacity() / 4) && (this.getCapacity() / 2 > 1)) {
            //预留一个不用的空间
            resize((this.getCapacity() + 1) / 2);
        }

        return res;//返回队首元素
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();

        if(this.isEmpty()){
            return null;
        }

        sb.append("队首>>> ");
        while (!this.isEmpty()){
            sb.append(this.deQueue()+",");
        }
        String str= sb.substring(0, sb.lastIndexOf(","));

        str+=" <<<队尾";

        return str.toString();
    }
}

测试

package com.company.project.subject.day2.queue;
public class LoopQueueTest {
    public static void main(String[] args) {

        LoopQueue<Integer> loopQueue = new LoopQueue<>();
        System.out.println("初始容量: "+loopQueue.getCapacity());

        for (int i = 0; i < 10; i++) {
            loopQueue.enQueue(i+1);
        }

        System.out.println("队满后扩容: "+loopQueue.getCapacity());
        for (int i = 0; i < 6; i++) {
            loopQueue.deQueue();
        }
        System.out.println("出队后缩容:"+loopQueue.getCapacity());
        System.out.println(loopQueue);
    }
}

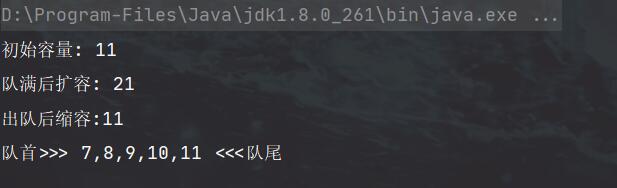
时间复杂度分析

• enqueue(E e) O(1)
• dequeue() O(1)
• getFront() O(1)
• getSize() O(1)
• isEmpty() O(1)

性能比较

package com.company.project.subject.day2.queue;

public class QueueCompare {
    public static void main(String[] args) {

        LoopQueue<Integer> loopQueue = new LoopQueue<>();
        long loopStart = System.nanoTime();
        for (int i = 0; i < 2000000; i++) {
            loopQueue.enQueue(i+10);
            if(i%3000==0){
                while (!loopQueue.isEmpty()){
                    System.out.println(loopQueue.deQueue());
                }
            }
        }
        while (!loopQueue.isEmpty()){
            System.out.println(loopQueue.deQueue());
        }
        long loopEnd = System.nanoTime();


        MyQueue<Integer> queue = new MyQueue<>();
        long start = System.nanoTime();
        for (int i = 0; i < 2000000; i++) {
            queue.enqueue(i+10);
            if(i%3000==0){
                while (!queue.isEmpty()){
                    System.out.println(queue.dequeue());
                }
            }
        }
        while (!queue.isEmpty()){
            System.out.println(queue.dequeue());
        }
        long end = System.nanoTime();

        System.out.println("循坏队列耗时: "+(loopEnd-loopStart)/1000000000.0);
        System.out.println("普通队列耗时: "+(end-start)/1000000000.0);

    }
}

运行:

队列应用

栈实现队列

剑指 Offer 09. 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof

class CQueue {

    //入队栈
    private Stack<Integer> stack1;
    //出队栈
    private Stack<Integer> stack2;

    public CQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }

    //入队
    public void appendTail(int value) {
        stack1.push(value);
    }

    /**
     * 出队
     * 栈2不为空返回栈顶元素
     * 栈1为空返回-1
     * 栈1不为将栈1元素弹出到栈2中,返回栈2栈顶元素
     * @return 队首元素,队空返回-1
     */
    public int deleteHead() {
        if(!stack2.isEmpty()){
            return stack2.pop();
        }
        if(stack1.isEmpty()){
            return -1;
        }else {
            while(!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
            return stack2.pop();
        }
    }
}

队列实现栈

225. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

• 实现 MyStack 类：

  void push(int x) 将元素 x 压入栈顶。
  int pop() 移除并返回栈顶元素。
  int top() 返回栈顶元素。
  boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/implement-stack-using-queues

package com.company.project.arithmetic.leetcode;
import java.util.LinkedList;
import java.util.Queue;

//用两个队列实现栈
public class MyStack225 {

    //与栈保持一致的队列
    Queue<Integer> queue1;
    //辅助队列
    Queue<Integer> queue2;

    public MyStack225() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }

    //入栈
    public void push(int x) {
        //将元素放入辅助队列
        queue2.offer(x);
        while (!queue1.isEmpty()){
            //栈(queue1)不为空时,将栈(queue1)中元素取出放入辅助队列
            queue2.offer(queue1.poll());
        }
        //交换两个队列
        Queue<Integer> queueTemp = queue1;
        queue1 = queue2;
        queue2 = queueTemp;
    }
	//出栈
    public int pop() {
        return queue1.poll();
    }
	//查看栈顶元素
    public int top() {
        return queue1.peek();
    }
	//判断栈是否为空
    public boolean empty() {
        return queue1.isEmpty();
    }
}