[数据结构与算法]线段树模板

概述

当需要对一个区间进行查询与修改时，常规的操作的时间复杂度为O(n)，其中n为区间长度。通过采用线段树这一数据结构，我们可以将时间复制度降低为O(nlogn)

以下是示意图:

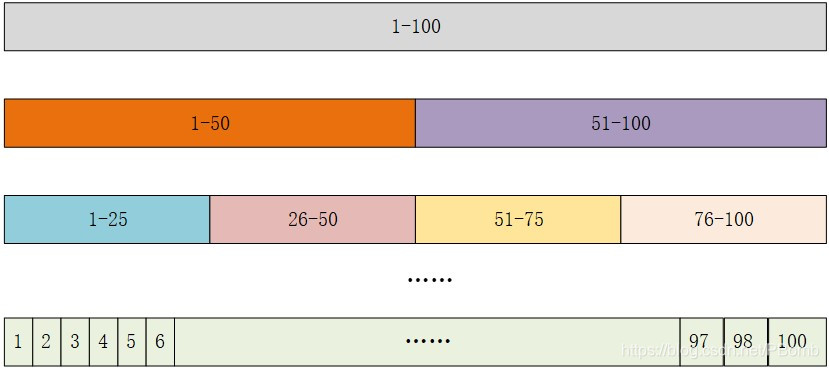
对于每个区间，我们用一个节点进行维护，我们可以继续向下划分得到子区间做为该节点的孩子节点，直到无法再向下划分。

这样每个区间的信息都可以从其子区间获取，而对于区间的修改，这需要对每个包含了该区间的节点进行修改。

ps:在为节点数组开空间时要开4n空间（n为区间长度），这是因为虽然最后一层有n个节点满二叉树只有2n-1个节点，但由于线段树维护的是区间，因此会出现空节点。
?

懒标记(lazy tag)

刚刚提到，对指定区间进行修改时需要对所有有关的区间进行修改，这样的时间开销会特别大。于是我们为可以区间的节点打上一个标记，记录下对当前区间的修改，而停止对其子节点进行修改过。
这里我采用的定义是：某个节点的标记是用于记录其子区间的。当这个节点的子节点要被查询或修改过时，便将懒标记下放，计算出子区间正确的值。

?

具体操作

线段树分别要实现以下几个操作

?

建树

void build(int u, int l, int r)
{
    if(l == r) {
        tr[u] = {l, r, num[l], 0};
    } else {
        int mid = l + r >> 1;
        tr[u].l = l, tr[u].r = r;
        build(u * 2, l, mid);
        build(u * 2 + 1, mid + 1, r);
        pushup(u);
    }
}

?

上传

void pushup(int u)
{
    tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum;
}

?

下放

void pushdown(int u)
{
    node& left = tr[u * 2];
    node& right = tr[u * 2 + 1];
    
    left.sum += tr[u].add * (left.r - left.l + 1);
    right.sum += tr[u].add * (right.r - right.l + 1);
    
    left.add += tr[u].add;
    right.add += tr[u].add;
    tr[u].add = 0;
}

?

修改

void modify(int u, int l, int r, int x)
{
    if(tr[u].l >= l && tr[u].r <= r) {
       tr[u].sum += (LL)x * (tr[u].r - tr[u].l + 1);
       tr[u].add += x;
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        
        if(l <= mid) {
            modify(u * 2, l, r, x);
        }
        
        if(r > mid) {
            modify(u * 2 + 1, l, r, x);
        }
        pushup(u);
    }
    
}

?

查询

LL query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) {
       return tr[u].sum; 
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        LL ans = 0;
        
        if(l <= mid) {
            ans += query(u * 2, l, r);
        }
        
        if(r > mid) {
            ans += query(u * 2 + 1, l, r);
        }
        return ans;
    }
}

?

模板题目（传送门）

完整代码

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

typedef long long LL;

int num[N];

struct node
{
    int l, r;
    LL sum, add;
}tr[4 * N];

void pushup(int u)
{
    tr[u].sum = tr[u * 2].sum + tr[u * 2 + 1].sum;
}

void pushdown(int u)
{
    node& left = tr[u * 2];
    node& right = tr[u * 2 + 1];
    
    left.sum += tr[u].add * (left.r - left.l + 1);
    right.sum += tr[u].add * (right.r - right.l + 1);
    
    left.add += tr[u].add;
    right.add += tr[u].add;
    tr[u].add = 0;
}

void build(int u, int l, int r)
{
    if(l == r) {
        tr[u] = {l, r, num[l], 0};
    } else {
        int mid = l + r >> 1;
        tr[u].l = l, tr[u].r = r;
        build(u * 2, l, mid);
        build(u * 2 + 1, mid + 1, r);
        pushup(u);
    }
}

LL query(int u, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) {
       return tr[u].sum; 
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        LL ans = 0;
        
        if(l <= mid) {
            ans += query(u * 2, l, r);
        }
        
        if(r > mid) {
            ans += query(u * 2 + 1, l, r);
        }
        return ans;
    }
}

void modify(int u, int l, int r, int x)
{
    if(tr[u].l >= l && tr[u].r <= r) {
       tr[u].sum += (LL)x * (tr[u].r - tr[u].l + 1);
       tr[u].add += x;
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        
        if(l <= mid) {
            modify(u * 2, l, r, x);
        }
        
        if(r > mid) {
            modify(u * 2 + 1, l, r, x);
        }
        pushup(u);
    }
    
}

int main()
{
    int n, m;
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++)
        cin >> num[i];
    
    build(1, 1, n);
    
    while(m--) {
        int t;
        cin >> t;
        if(t == 1) {
            int x, y, k;
            cin >> x >> y >> k;
            modify(1, x, y, k);
        } else {
            int x, y;
            cin >> x >> y;
            cout << query(1, x, y) << endl;
        }
    }
    
    return 0;
}