线性表的表示和实现
1.线性表的特点和基本操作
线性表的基本特点
1.集合中必存在唯一的一个“第一元素”。2.集合中必存在唯一的一个 “最后元素” 。
3.除最后一个元素之外,均有唯一的后继。
4.除第一个元素之外,均有唯一的前驱。
线性表、包括顺序表和链表,顺序表里面元素的地址是连续的。链表里面节点的地址不是连续的,是通过指针连起来的。
线性表的基本操作
-
InitList(&L)
操作结果:构造一个空的线性表L。 -
DestroyList(&L)
初始条件:线性表L已存在。
操作结果:销毁线性表L。 -
ListEmpty(L)
初始条件:线性表L已存在。
操作结果:若L为空表,则返回TRUE,否则返回FALSE。 -
ListLength(L)
初始条件:线性表L已存在。
操作结果:返回L中数据元素的个数。 -
GetElem(L, i, &e)
初始条件:线性表L已存在, 1≤i ≤ ListLength(L) 。
操作结果:用e返回L中第i个数据元素的值。 -
LocateElem(L, e, compare())
初始条件:线性表L已存在,compare()是数据元素判定函数。
操作结果:返回L中第1个与e满足compare( )的数据元素的位序。若这样的元素不存在,则返回值为0。 -
PriorElem(L, cur_e, &pre_e )
初始条件:线性表L已存在。
操作结果:若cur_e是L中的数据元素,且不是第一个,则用pre_e返回它的前驱,否则操作失败,pre_e无定义。 -
NextElem(L, cur_e, &next_e)
初始条件:线性表L已存在。
操作结果:若cur_e是L中的数据元素,且不是最后一个,则用next_e返回它的后继,否则操作失败,next_e无定义。 -
ListTraverse(L, visit( ))
初始条件:线性表L已存在。
操作结果:依次对L中的每个数据元素调用函数visit( )。一旦visit( )失败,则操作失败。
/* 以上除了初始化和销毁操作其他都是引用型操作 */ -
ClearList(&L)
初始条件:线性表L已存在。
操作结果:将L重置为空表。 -
ListInsert(&L, i, e)
初始条件:线性表L已存在,1≤i≤Listlength(L)+1。
操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1。 -
ListDelete(&L, i, &e)
初始条件:线性表L已存在且非空,1≤i≤Listlength(L)。
操作结果:删除L中第i个数据元素,并用e返回其值,L的长度减1。
}ADT List
2.线性表的顺序表示和实现
①顺序表的存储结构
#define MAXSIZE 100 //顺序表的最大容量
typedef struct{
ElemType *elem; //顺序表在内存的基址
int length; //当前顺序表的长度,即表中存放元素的个数
}SqList; //顺序表的结构类型名为SqList
②初始化InitList
1. 初始化:创建一个空的顺序表
Status InitList(SqList &L) { //构造一个空的顺序表L
L.elem=new ElemType[MAXSIZE];
if(!L.elem) exit(OVERFLOW); //分配失败
L.length=0; //空表长度为0
return OK;
} //InitList
③取值GetElem
2. 取值:获取表中第i个数据元素的值
Status GetElem(SqList L, int i, ElemType &e){
//若i<1或i大于表长,返回ERROR;否则用e返回第i个元素的值,并返回OK
if(i<1||i>L.length) return ERROR; //i值不合法,返回ERROR
e=L.elem[i-1]; //将第i个元素值赋给e
return OK;
}//GetElem
基本操作:元素的赋值
赋值次数:1
时间复杂度:O(1)
④修改ModifyElem
修改:将表中第i个数据元素的值改为指定值
status ModifyElem(SqList &L, int i, ElemType e){
//在顺序表L中修改第i个元素,且1≤i≤ListLength_Sq(L)
if(i<1||i>L.length) return ERROR; //i值不合法,返回ERROR
*(L.elem+i-1) =e; //将指定元素值赋给第i个元素
return OK;
}//ModifyElem
基本操作:元素的赋值
赋值次数:1
时间复杂度:O(1)
⑤查找LocateElem
3.查找:查找指定元素e
int LocateElem(SqList L, ElemType e){
//在顺序表L中查找第1个值与e相等的元素的位序,若找到,返回其在L中的位序,否则返回0。
for(i=0;i<L.length;i++) if(e==L.elem[i]) return i+1;
return 0;
} //LocateElem
基本操作:元素的比较
最坏情况下比较的次数:n
平均比较次数:(n+1)/2
时间复杂度:O(n)
⑥插入ListInsert
4. 插入:将指定元素e插入到指定位置
Status ListInsert ( SqList &L, int i, ElemType e) {
//在顺序表L的第i个位置插入新的数据元素e,且1≤i≤ListLength(L)+1
if(i<1||i>L.length+1) return ERROR;
if(L.length==MAXSIZE) return ERROR; //当前存储空间已满
for(j=L.length-1; j>=i-1; j--)
L.elem[j+1]=L.elem[j]; //插入位置及其后的元素后移
L.elem[i-1]=e; //插入元素e
L.length++; //表长加1
return OK;
} //ListInsert
基本操作:元素的移动
最坏情况下移动的次数:n
平均移动次数: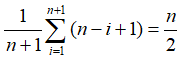
时间复杂度:O(n)
⑦删除ListDelete
5. 删除:将指定位置元素e删除
操作特点:插入位置后面的元素均需前移一个位置
合法的删除位置:1≤i≤ListLength(L)
Status ListDelete(SqList &L, int i) {
//在顺序表L中删除第i个元素并用e返回其值,且1≤i≤ListLength_Sq(L)
if(i<1||i>L.length) return ERROR; //删除位置不合法
for(j=i; j<=L.length-1; j++)
L.elem[j-1]=L.elem[j]; //被删除元素之后的元素向前移一个位置
--L.length; //表长减1
return OK;
} //ListDelete
基本操作:元素的移动
最坏情况下的移动次数:n-1
平均移动次数: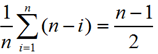
时间复杂度:O(n)
3.线性表的链式表示和实现
①链式存储结构特点
链式存储结构特点:用一组任意的存储单元存储线性表的数据元素(这组存储单元可以连续,也可以不连续)。
? 单链表可由一个头指针唯一确定。
? 若要访问数据元素ai,须从头指针出发,顺着指针域逐个访问,直至第i个结点。因此,线性表的链式存储结构只适合顺序访问,不支持直接访问。
单链表有两种形式:不带头结点的单链表和带头结点的单链表。
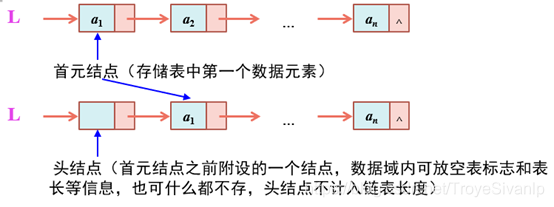
②单链表的存储结构
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //直接后继:指向下一个结点的指针
}LNode, *LinkList;
③初始化InitList
1. 初始化:创建一个带头结点的空链表
status InitList(LinkList &L) { //构造一个空的链表L
L=new LNode; //生成新结点
if(!L) exit(OVERFLOW); //分配失败
L->next=NULL; //空表长度为0
return OK;
} //InitList
④取值GetElem

//L为带头结点的单链表头指针,当第i个元素存在时,其值赋给e并返回OK,否则返回ERROR
status GetElem(LinkList L, int i, ElemType &e) {
p=L->next; j=1; //p指向首元结点,j为计数器
while( p&&j<i ) { p=p->next; ++j; } //顺指针向后查找直至第i个元素或表尾
if( !p || j>i )return ERROR;
e=p->data;
return OK;
} //GetElem_L
基本操作:指针后移
若1≤i≤n,指针移动i-1次,否则移动0次或n次
最坏情况下移动的次数:n(表中不存在第i个元素时)
时间复杂度:O(n)
⑤查找
3. 查找:查找链表中与给定元素e的值相等的元素的位置
LNode *LocateElem(LinkList L, ElemType e){
//在带头结点的单链表L中查找第1个数据元素为e的,若找到则返回该元素结点的地址(指针类型),否则返回NULL。
p=L->next; //p指向首元结点
while( p&&p->data!=e ) p=p->next;
return p;
} //LocateElem_L
基本操作:元素的比较
最坏情况下的比较次数:n
平均比较次数:(n+1)/2
时间复杂度:O(n)
⑥插入ListInsert
4. 插入:将值为e的元素插入到指定位置
status ListInsert( LinkList &L, int i, ElemType e){
//在带头结点的单链表L中第i个位置之前插入元素e,1≤ i≤表长+1
p=L; j=0;
while( p&&j<i-1 ) { p=p->next; j++; } //顺指针找第i-1个结点
if( !p || j>i-1 ) return ERROR; //i大于表长加1或i小于1
s=new LNode; //生成新结点
s->data=e;
s->next=p->next; //插入L中
p->next=s;
return OK;
} //ListInsert
基本操作:指针后移
当1≤i ≤表长+1时,指针后移i-1次,否则,后移0或n+1次
时间复杂度:O(n)
⑦删除ListDelete
5. 删除:删除指定位置/值的元素
status ListDelete(LinkList &L, int i, ElemType &e) {
//在带头结点的单链表L中,删除第i个元素,并用e返回其值
p=L; j=0;
while( p->next && j<i-1 ) {p=p->next; j++;} //顺指针找第i-1个结点
if( !(p->next) || j>i-1 ) return ERROR; //i小于1或i大于表长
q=p->next; //q指向第i个结点
p->next=q->next;
e=q->data;
free(q); //释放所删结点的空间
return OK;
} //ListDelete
基本操作:指针后移
当1≤i ≤表长时,指针后移i-1次,否则后移0或n次
时间复杂度:O(n)
⑧创建单链表CreatList_R
6. 创建单链表:后插法
void CreatList_R(LinkList &L, int n) {
//正位序输入n个元素的值,建立带头结点的单链线性表L
L=new LNode;
L->next=NULL; //空链表
q=L;
for(i=0; i<n; i++){
p= new LNode;
cin>> p->data;
p->next=NULL;
q->next=p; //将新结点插入在表尾
q=p;
}
} //CreatList_R
⑨双向链表的存储结构
typedef struct DuLNode{
ElemType data; //数据域
struct DuLNode *prior; //直接前驱
struct DuLNode *next; //直接后继
}DuLNode, *DuLinkList;
⑩双向链表插入节点ListInsert_DuL
status ListInsert_DuL (DuLinkList &L, int i, ElemType e) {
//在带头结点的双向循环链表L中第i个位置之前插入元素e,i的合法值为1≤i ≤表长加1。
p=L->next; j=1;
while(p!=L&&j<i) {p=p->next; j++; }
//查找第i个结点的位置,即插入位置,而不是找前驱结点
if(j!=i) return ERROR; //i值不合法
s=new DuLNode; //生成新结点
s->data=e;
s->prior=p->prior; p->prior->next=s; //插入
s->next=p; p->prior=s;
return OK;
} //ListInsert_DuL
⒒双向链表删除节点
status ListDelete_DuL(DuLinkList &L, int i, ElemTypw &e) {
//删除带头结点的双向循环链表中第i个元素,i的合法值为1≤i ≤表长
p=L->next; j=1;
while(p!=L&&j<i) {p=p->next; j++;}
//查找第i个结点的位置,即插入位置,而不是找前驱结点
if(p==L||j>i) return ERROR; //i值不合法
e=p->data;
p->prior->next=p->next; //删除第i个结点
p->next->prior=p->prior;
free(p); //释放结点空间
return OK;
} //ListDelete_DuL
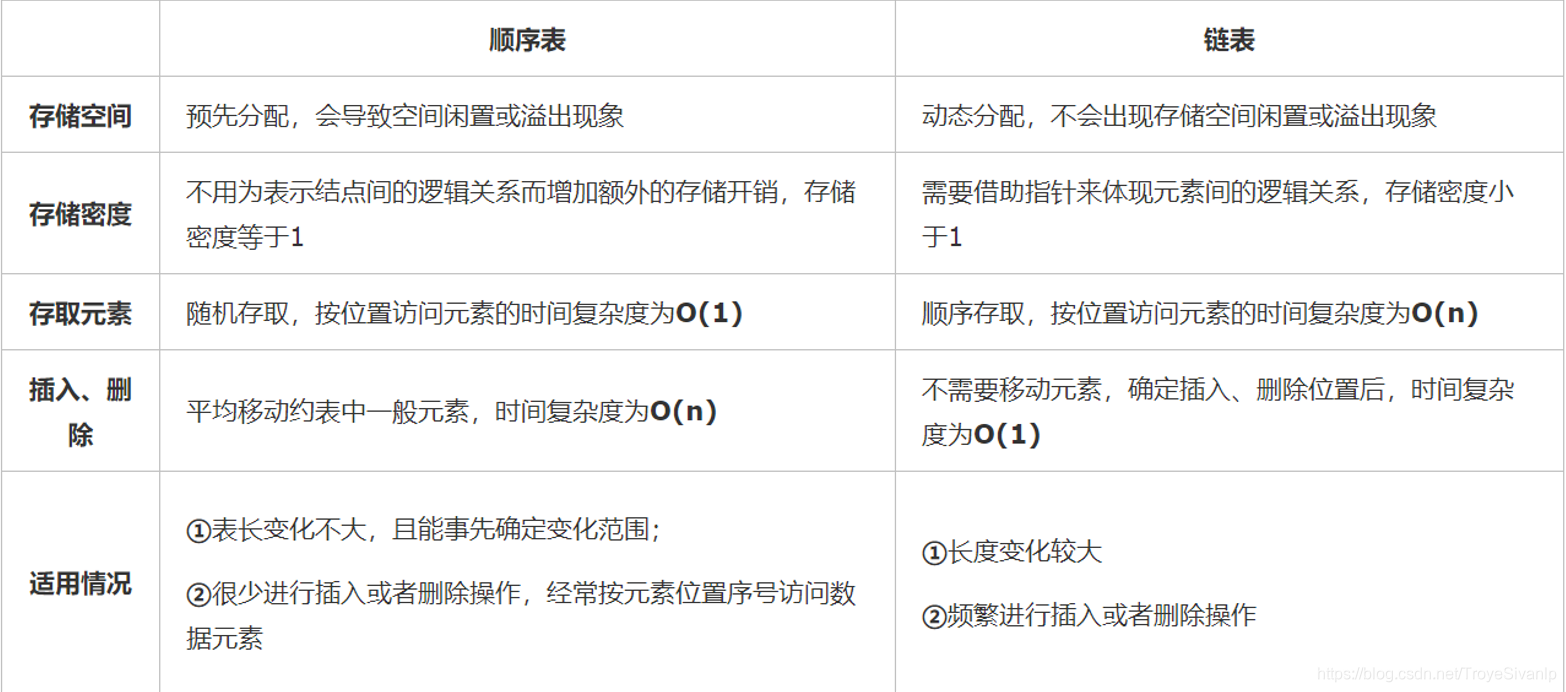
4.顺序表和链表的比较