如果只有一个自变量X,而且因变量Y和自变量X之间的数量变化关系呈近似线性关系,就可以建立一元线性回归方程,由自变量X的值来预测因变量Y的值,这就是一元线性回归预测。
数据:
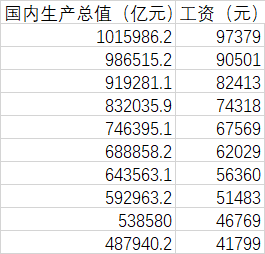
拟合数据如下,我们要根据国内国内生产总值,预测工资
下面展示一些 需要的第三方库。
import pandas as pd #read_excel,读入excel中的数据
import matplotlib.pyplot as plt #绘制回归曲线
from sklearn.linear_model import LinearRegression #包含通过最小二乘法,建立线性回归方程的系数的第三方库
将excel表中的数据读到data变量中,data为一个dataframe类型框架,并利用data初始化x,y
data = pd.read_excel("F:/数据测试.xlsx") # 参数为excel文件的路径
x_国内生产总值 = data["国内生产总值(亿元)"].values.reshape(-1, 1) #将其转化为列向量
y_工资 = data["工资(元)"].values.reshape(-1, 1)#将其转化为列向量
然后对建立一元线性模型,并拟合数据
reg = LinearRegression() #建立一元线性模型
model = reg.fit(x_国内生产总值, y_工资) #拟合数据
然后对样本中的值,进行预测,并绘制出图像
predictions = model.predict(x_国内生产总值) # 对样本中的值,进行预测
plt.plot(x_国内生产总值, predictions) # 绘制回归曲线
plt.title("GDP-Time") #图像的标头
plt.xlabel("国内生产总值(/亿元)") # x轴标签
plt.ylabel("工资(/元)") # y轴标签
plt.show() #显示图像
然后我们运行程序,就得到了以下回归方程曲线

我们可以再加入原始数据的散点图,看起来可视化程度会更高!
plt.scatter(x_国内生产总值, y_工资) # 此行代码要加在 plt.show() 之前
点击运行,结果如下:

至此,一元函数的线性回归就暂时告一段落了(后面可能会对计算一元线性回归的拟合优度,判断线性回归方程是否合理进一步叙述,今天先从简单的开始),在实践中学习,由易到难,欢迎点赞,评论,一起交流!