一、树
双亲表示法: 顺序存储各个结点时,给各个结点添加一个变量,记录其父结点的位置。
孩子表示法: 建立多个指针域,指向它所有子节点的地址,任何一个结点都会掌握他所有子节点的信息。
孩子兄弟表示法: 从树的根结点开始依次采用链表去存储各个结点的孩子结点和兄弟结点,可以把一颗普通的树转换为二叉树。
二、二叉树
1. 定义
二叉树:树中每个结点最多只能由两个字结点。
- 在二叉树中,第i层上最多有2^(i-1)
- 在二叉树中,如果深度为k,那么最多有 (2^k)-1 个结点
- 满二叉树:在一颗二叉树中,所有分支节点都存在在左子树和右子树,而且叶子都在同一层上。
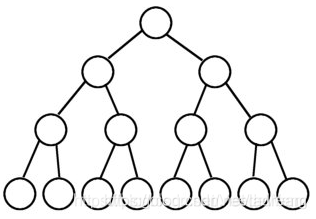
- 完全二叉树:除去最后一层之外,每一层上的结点数均达到最大值,最后一层只缺少最右边的若干节点,满二叉树一定是完全二叉树,反过来不一定成立。
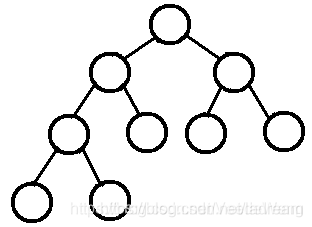
三、二叉搜索树
1.定义
二叉搜索树:binary serach tree(BST),二叉查找树、二叉排序树。二叉搜索树其实就是普通的二叉树上加了一些限制。
二叉树对于结点时没有任何限制的,但是在二叉搜索树中插入子节点的由一些特殊的要求:
- 非空左子树的所有键值都小于根节点的键值
- 非空右子树的所有键值都大于其根节点的键值
- 左右子树本身也都是二叉搜索树
二叉搜索树的特点:相对较小的值总是保存在子结点上,相对较大的值总是保存在右节点上。
2.实现
// 结点
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
}
}
// 二叉搜索树,相对较小的值存在左边,相对较大的存在最右边
class BinarySearchTree {
constructor() {
// 根结点
this.root = null
}
// 插入值
insertNode(node, newnode) {
// 右边
if (newnode.value > node.value) {
// 原来右边的子结点没有数据
if (node.right === null) {
node.right = newnode
}
else {
this.insertNode(node.right, newnode)
}
}
else if (newnode.value < node.value) {
// 原来左边的子结点没有数据
if (node.left === null) {
node.left = newnode
}
else {
this.insertNode(node.left, newnode)
}
}
}
// insert
insert(value) {
let newNode = new Node(value)
// 空间
if (this.root === null) {
this.root = newNode
} else {
this.insertNode(this.root, newNode)
}
}
}
const bst = new BinarySearchTree()
bst.insert(5)
bst.insert(3)
bst.insert(6)
bst.insert(4)
console.log(bst)
3.遍历
(1)先序遍历
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
// 先序遍历
preOrderTravelsal(cb) {
this.preOrderTravelsalNode(this.root, cb)
}
preOrderTravelsalNode(node, cb) {
if (node === null) return
// 打印
cb(node.value)
this.preOrderTravelsalNode(node.left, cb)
this.preOrderTravelsalNode(node.right, cb)
}
const rst = []
const cb = (value) => {
rst.push(value)
}
const bst = new BinarySearchTree()
bst.insert(11)
bst.insert(7)
bst.insert(15)
bst.insert(5)
bst.insert(9)
bst.insert(3)
bst.insert(9)
bst.preOrderTravelsal(cb)
console.log(rst) //[ 11, 7, 5, 3, 9, 15 ]
(2)中序遍历
- 递归遍历左子树
- 访问父亲
- 递归遍历右子树
// 中序遍历
inOrder(cb) {
this.inOrderNode(this.root, cb)
}
inOrderNode(node, cb) {
if (node === null) return
this.inOrderNode(node.left, cb)
cb(node.value)
this.inOrderNode(node.right, cb)
}
(3)后序遍历
- 后续遍历左子树
- 后续遍历右子树
- 访问父亲
// 后序遍历
postOrder(cb) {
this.postOrderNode(this.root, cb)
}
postOrderNode(node, cb) {
if (node === null) return
this.postOrderNode(node.left, cb)
this.postOrderNode(node.right, cb)
cb(node.value)
}
(4)最大值、最小值、查找
// 最大值
max() {
let node = this.root
// 最右边的结点就是最大的值
while (node.right !== null) {
node = node.right
}
return node.value
}
// 最小值
min() {
let node = this.root
// 最右边的结点就是最大的值
while (node.left !== null) {
node = node.left
}
return node.value
}
// 寻找特定的值
search(val) {
let node = this.root
while (node !== null) {
if (node.value > val) {
node = node.left
}
else if (node.value < val) {
node = node.right
}
else {
return true
}
}
}
四、平衡二叉树
1.定义
二叉平衡树: 又称平衡二叉搜索树,也叫AVL树,是一种自平衡的树。
除了规定的左节点小于根结点,右结点大于根结点外,还规定了左子树和右子树的高度差不得超过1
平衡因子: 左子树的高度减去右子树的高度。
所以平衡二叉树中,平衡因子的绝对值<=1时,可以满足二叉平衡树的需求。 如果平衡因子的绝对值超过了1,那么我们就称之为:失衡,结点需要随时添加、随时删除。
控制平衡因子: 旋转结点。向左单旋转、向左双旋转、向右单旋转、向右双旋转
五、红黑树
1.定义
AVL树相对于红黑树它的插入、删除操作效率都不高。
红黑树:是一种自平衡的二叉搜索树,以前叫平衡二叉B树,R-B tree
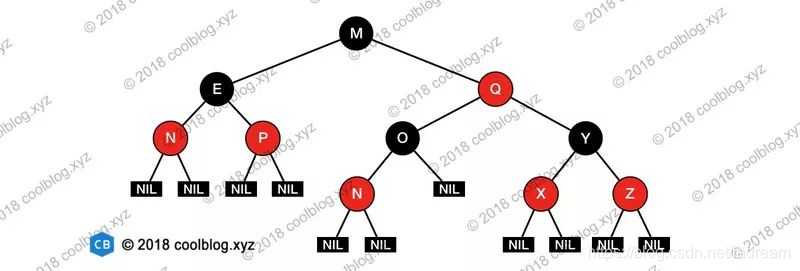
2.特性
这五条是必须遵守的规则,保障了从根节点到叶子结点的最长路径不大于最短节点的2倍
- 结点是红色或黑色(给结点设置color属性)
class Node{
constructor(){
this.color = 'black'
}
}
- 根节点是黑色
- 叶子结点都是黑色,且为null(NIL结点)
- 红色节点的父结点都是黑色,红色结点的子结点都是黑色
- 从任意结点出发,到其每个叶子结点的路径中包含相同数据的黑色结点
- 红黑树插入数据时会先去遍历数据应该插入到哪个位置,插入的数据一定是红色