
一、认识平衡二叉树
前几天,我们将搜索二叉树(也称为二叉排序树)讲解了,重点讲了搜索二叉树的插入和删除操作,由特别是删除操作,是比较难的知识点。现在我们将继续在搜索二叉树的基础之上,学习一颗新的数,那就是大名鼎鼎的平衡二叉树(AVL树)。在学习平衡二叉树前,同学们需掌握了搜索二叉树的基本操作之后,再来看平衡二叉树的知识,就会简单一点哦!!!
前期文章:二叉树的概念以及搜索二叉树。
本期文章:GitHub源码链接。
我们前面讲了搜索二叉树的定义:一个节点的左子节点的关键字值小于这个节点,右子节点的关键字值大于或等于这个父节点。简单点说就是左边的小,右边的大。现在我们试着将这个数组插入到搜索二叉树,看看是什么样子?
int[] array = {1,2,3,4,5,6,7,8}; //升序
当我们试着去插入后,会发现,这颗搜索二叉树有一点怪怪,如图:
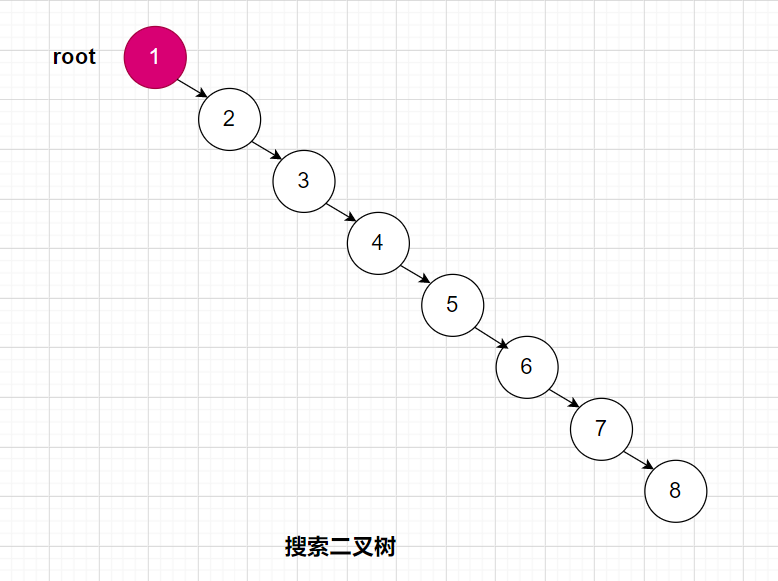
根据上面的图,我们可以看出,当我们去对一个本身已经有序的数组,去插入到搜索二叉树中,结果却跟“链表”长得更相似。也就是说,假设我们需要查找8,这颗搜索二叉树的时间复杂度就跟链表一样,是O(N)了。所以怎么办??? 就出现了今天的主题:平衡二叉树。
要想使时间复杂度降下来,我们就得调整这棵树的“样子”,使之查找元素的时间复杂度,跟这棵树的深度直接挂钩,直接变为O(logN)。所以我们得从添加元素的时候着手。平衡二叉树代码的整体框架,跟搜索二叉树差不多,如下:
class TreeNode {
public int val;
public int height; //新加的成员变量:节点高度
public TreeNode left;
public TreeNode right;
public TreeNode(int val) {
this.val = val;
this.height = 1; //新节点的初始高度为1
}
}
public class AVL{
private TreeNode root; //根结点
public void add(int val) { //插入新的节点
}
public void remove(int val) { //删除对应的节点
}
public boolean contains(int val) { //查询是否有该值
}
}
二、插入操作
首先,平衡二叉树与搜索二叉树的差别在于:平衡二叉树,它自己可以自动调节整棵树的平衡,也叫自平衡机制。 所以在平衡二叉树里,有一个概念叫做平衡因子,意思就是: 对于每一个子树而言,它的左子树的高度 减去 右子树的高度 ,差值的绝对值不能超过1;换句话说就是:两边高度相减的范围必须在[-1,1],这个区间呢,才能称为平衡。这也是我们为什么在TreeNode类里面加入了height这个变量的原因。
插入操作,我们只需掌握4种不同情况导致的不平衡。分别是 LL型、RR型、LR型和RL型。
-
LL型
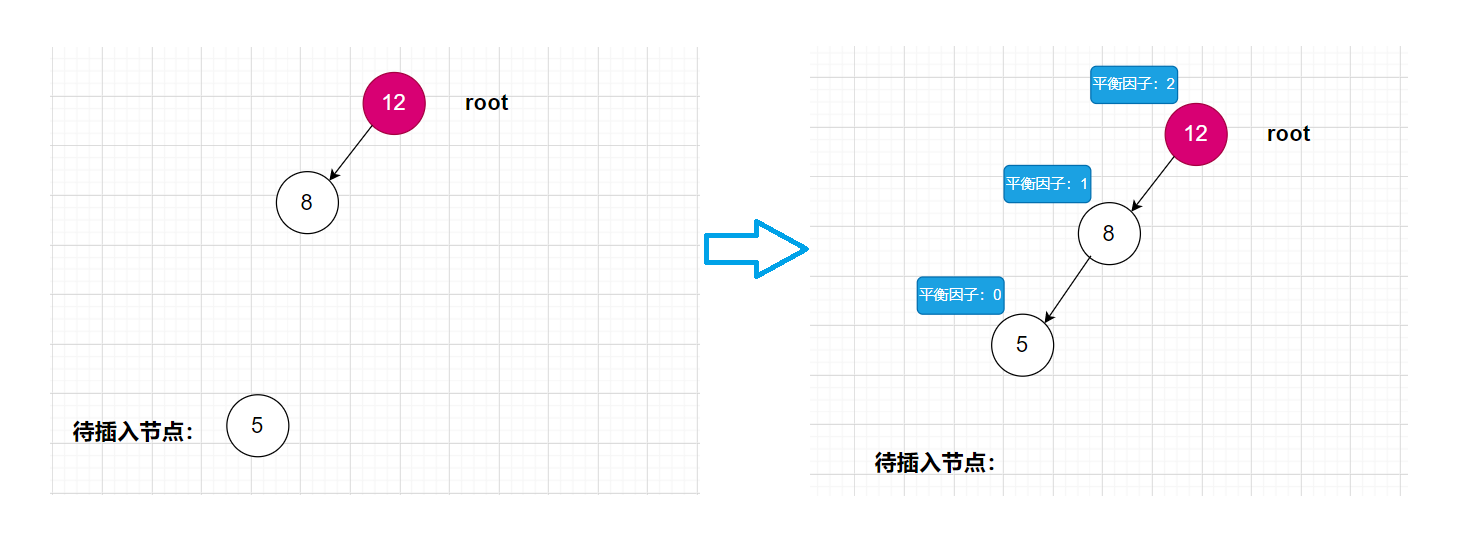
就如上面这幅图所示,当我们插入5节点后,计算平衡因子,我们就会发现,在12结点处的平衡因子超过了1,所以我们需要对12这个节点进行调整。正是因为2节点的插入,从而导致了12节点的不平衡,而5节点在12节点的左子树(8节点)的左子树(5节点)。所以这种情况就叫LL型。我们稍微将上面的图再“装饰”一下,将它们各自的子节点都显示出来,如下图:(注:T1~T4,在实际的情况中可能没有,此时是为了让大家更好理解如何去进行旋转操作,才加上的)
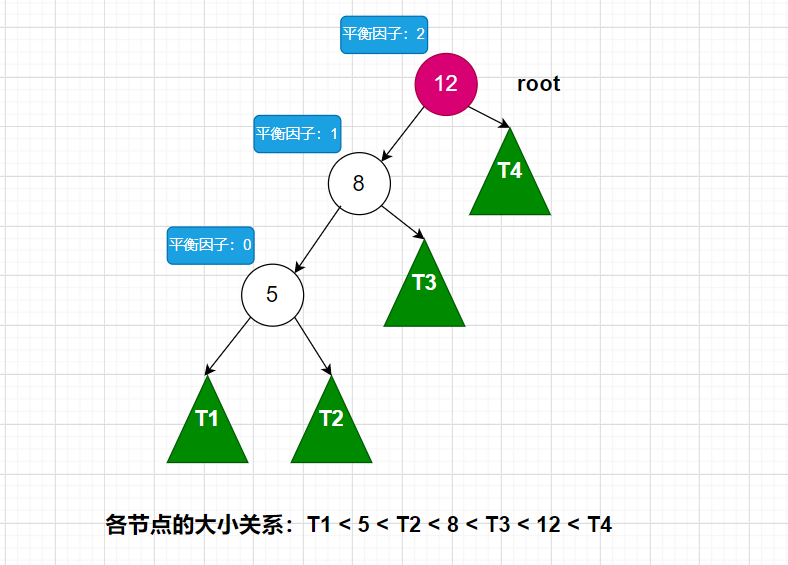
LL型动图
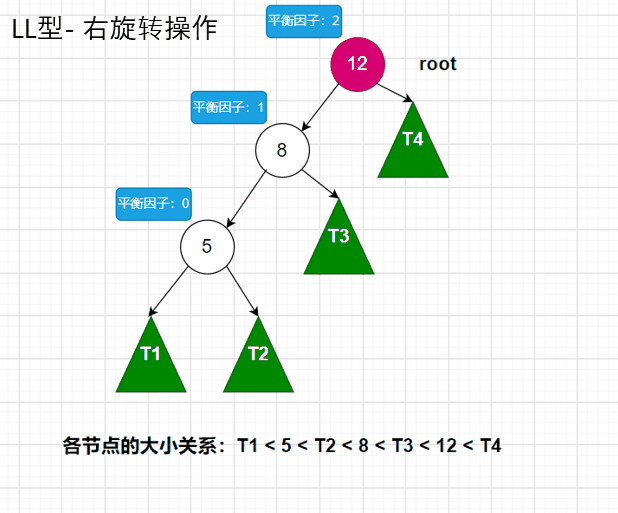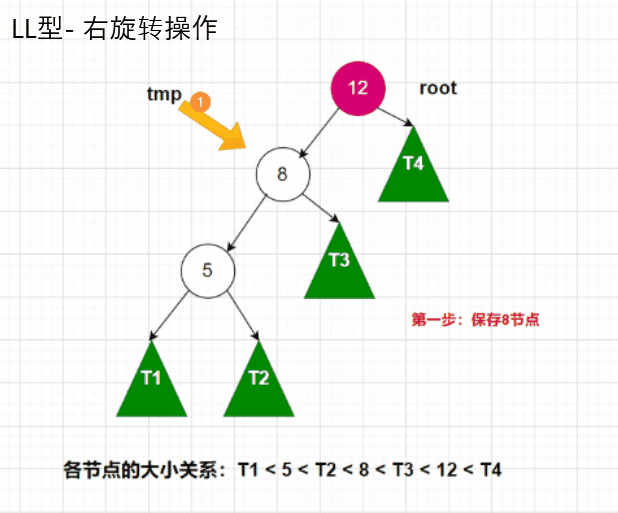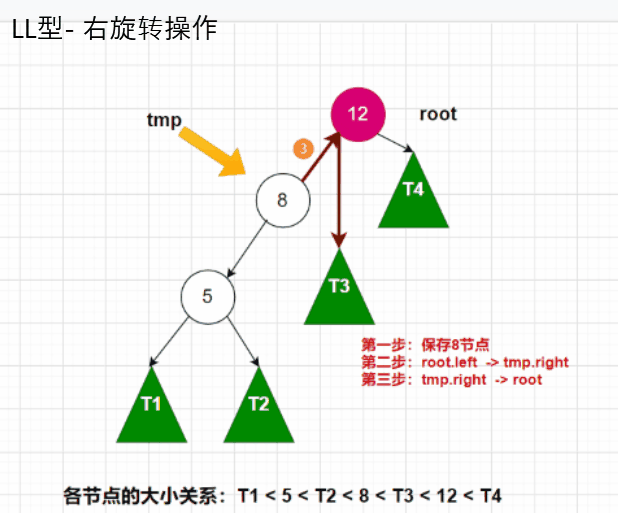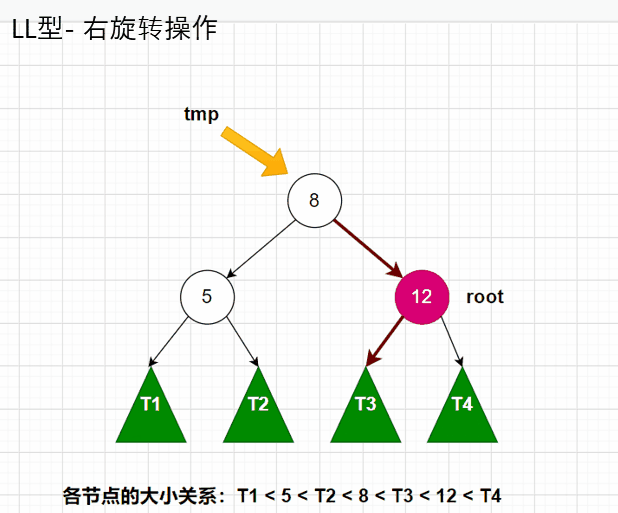
对于LL型,我们需要进行右旋转操作,同学们根据动图,自行在纸上画一下是如何进行连接的,就能更好的理解其中的关系。代码图如下:

最后,我们还要再说一下,旋转之后,只有两个节点的高度是需要更改的,就是root和tmp这两个节点的高度,等于它左右子树的高度,再加上自己本身的高度值1,就是旋转之后,这个节点的新高度了。切记:必须先计算root的高度之后,才能计算tmp的高度,因为root是tmp的右子树,tmp的高度是依赖于root的高度值。
-
RR型
讲完了LL型,RR型,也就简单了许多,RR型和LL型是差不多的。只是二者互为镜像而已。我们就直接看动图吧!
RR型动图
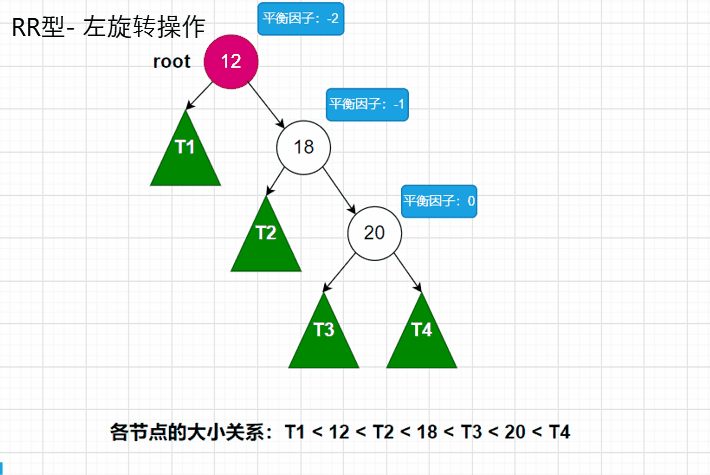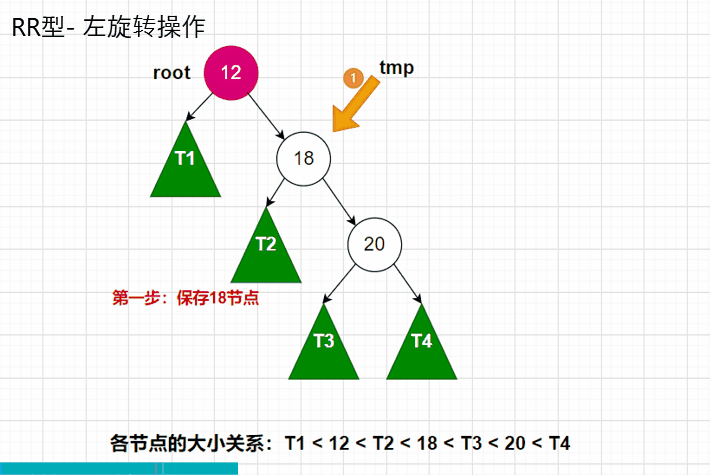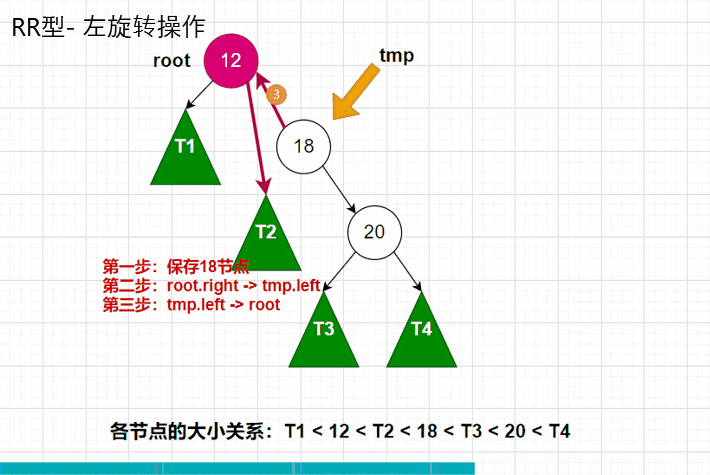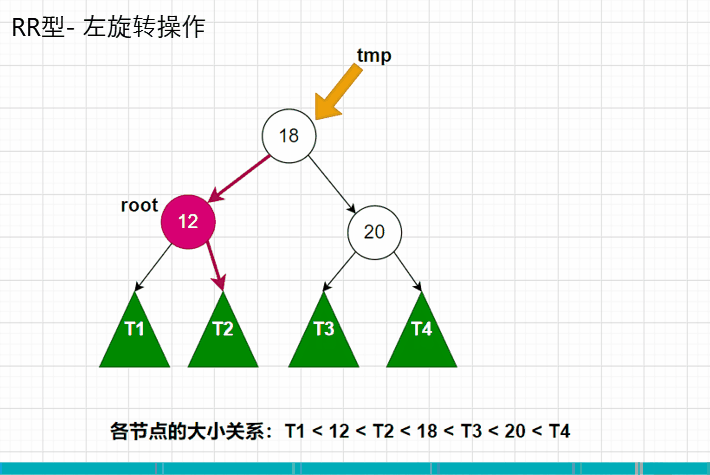
计算高度的节点还是root和tmp这两个节点,还是先计算root的高度,再计算tmp的高度。代码图如下:
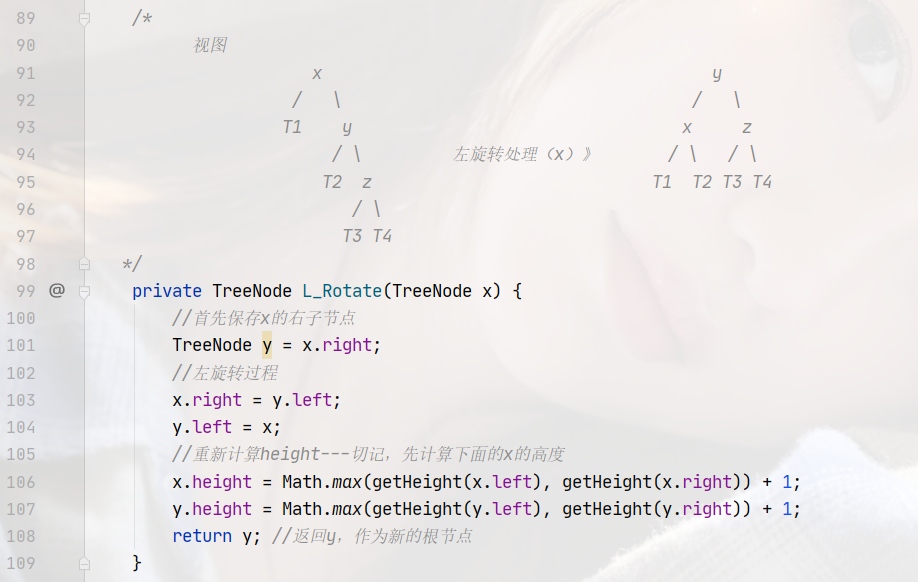
-
LR型
讲完了LL型和RR型,接来了的LR和RL型,就非常简单,因为LR和RL,根本不需要重新再写新的方法,我们只需要旋转两次,就是LR或者RL的操作,多的不说,我们以图为切入点,展开来讲;
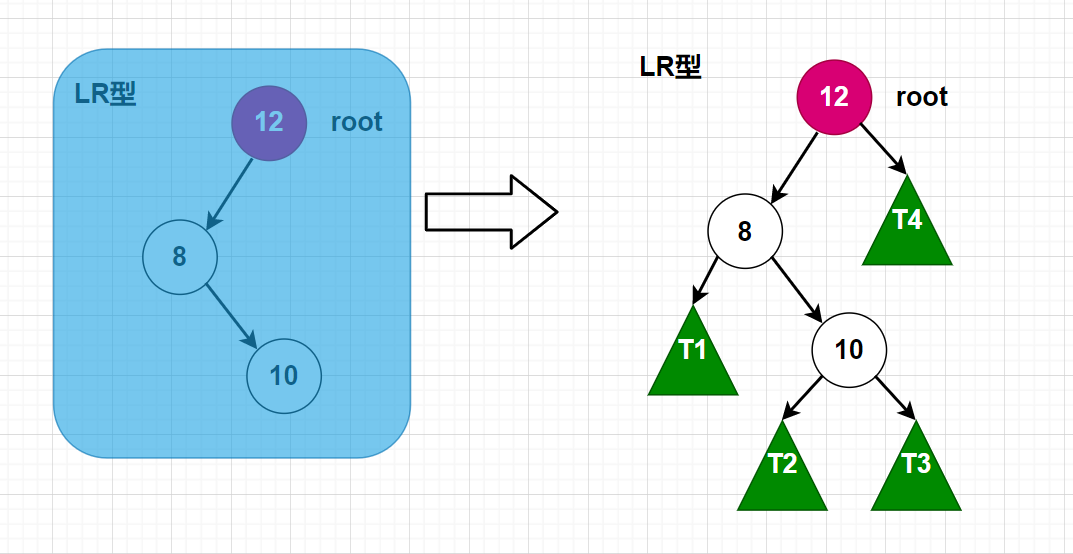
上图就是LR型的情况,当我们尝试着上面的LL型和RR型,发现是解决不了问题的。我们只有想办法让LR型转化成LL型,问题就迎刃而解了。问题在于怎么转化? 来,我们看下图:
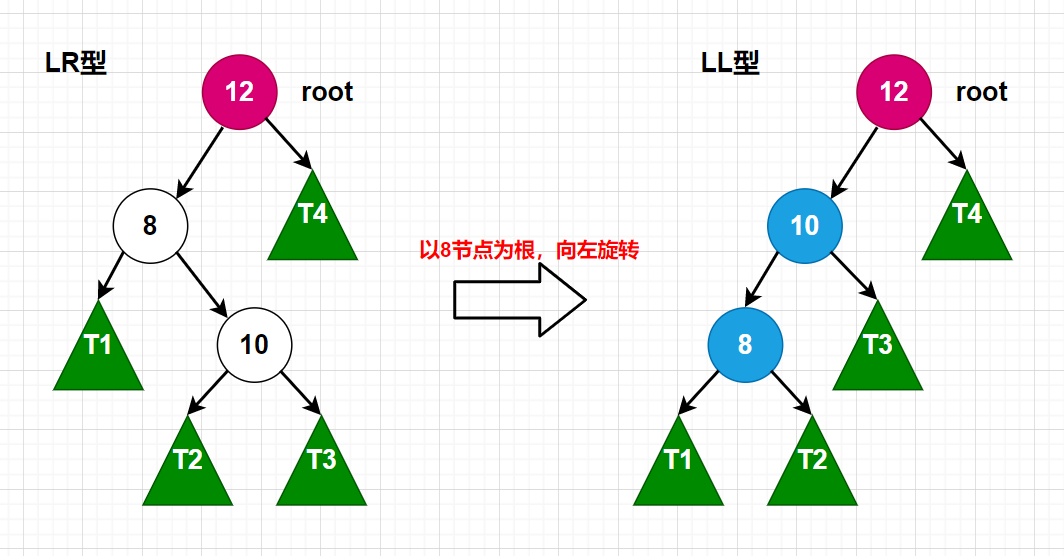
我们可以发现,我们只需将8节点先向左旋转一下,就能得到LL型的状态。得到LL型后,问题就回到了LL型上,那我们再整体向右旋转一次,就能达到平衡的效果。我们以动图来演示一下:
LR型动图
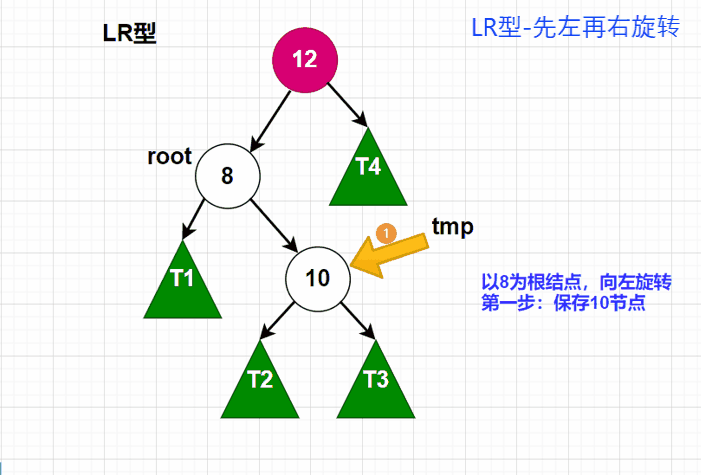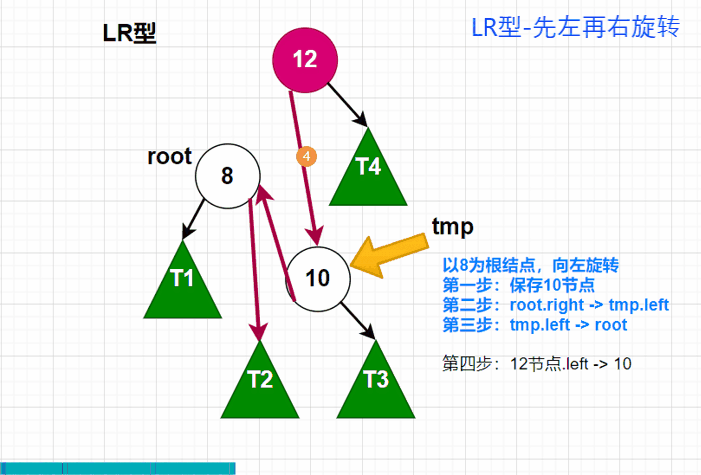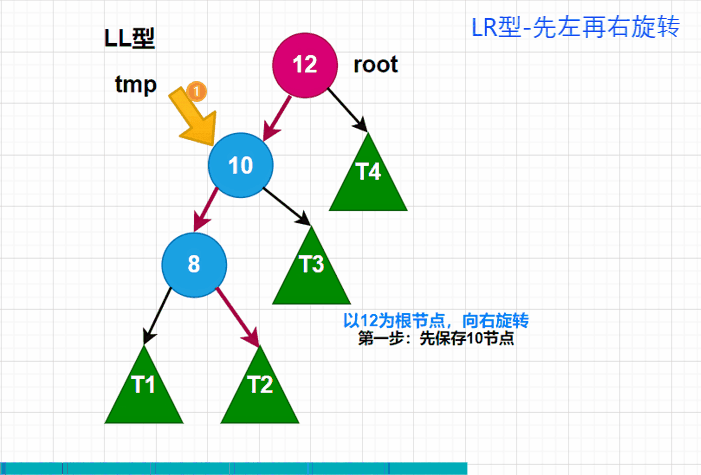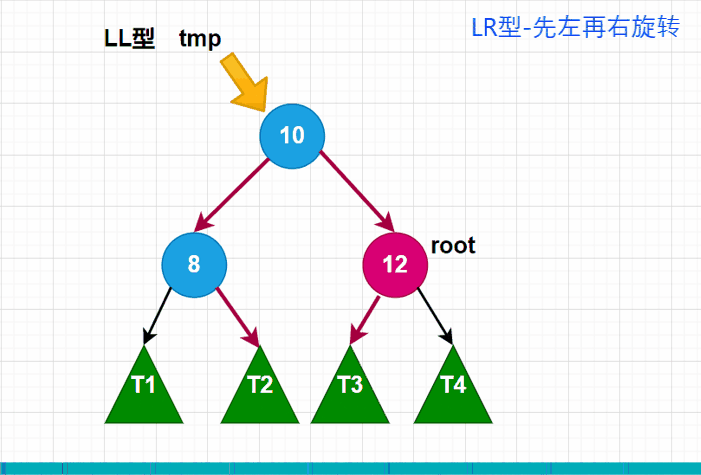
-
RL型
相应的RL型,跟LR型也是差不多,就是镜像而已。
LR是先左旋转再右旋转,而RL是先有旋转再左旋转。我们还是以图来展开说明吧!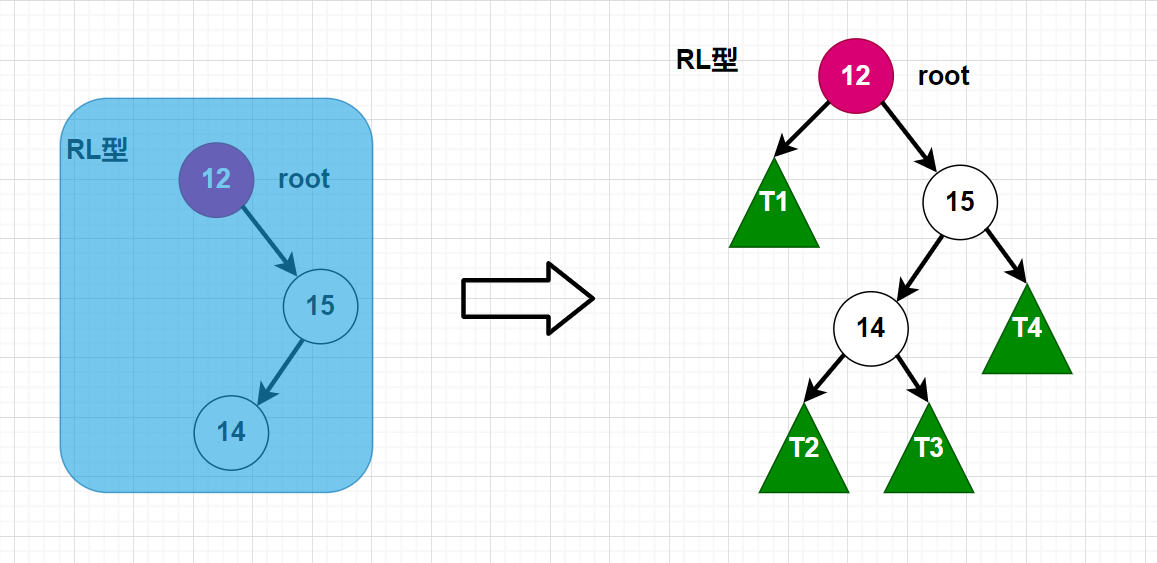
旋转过程如下:
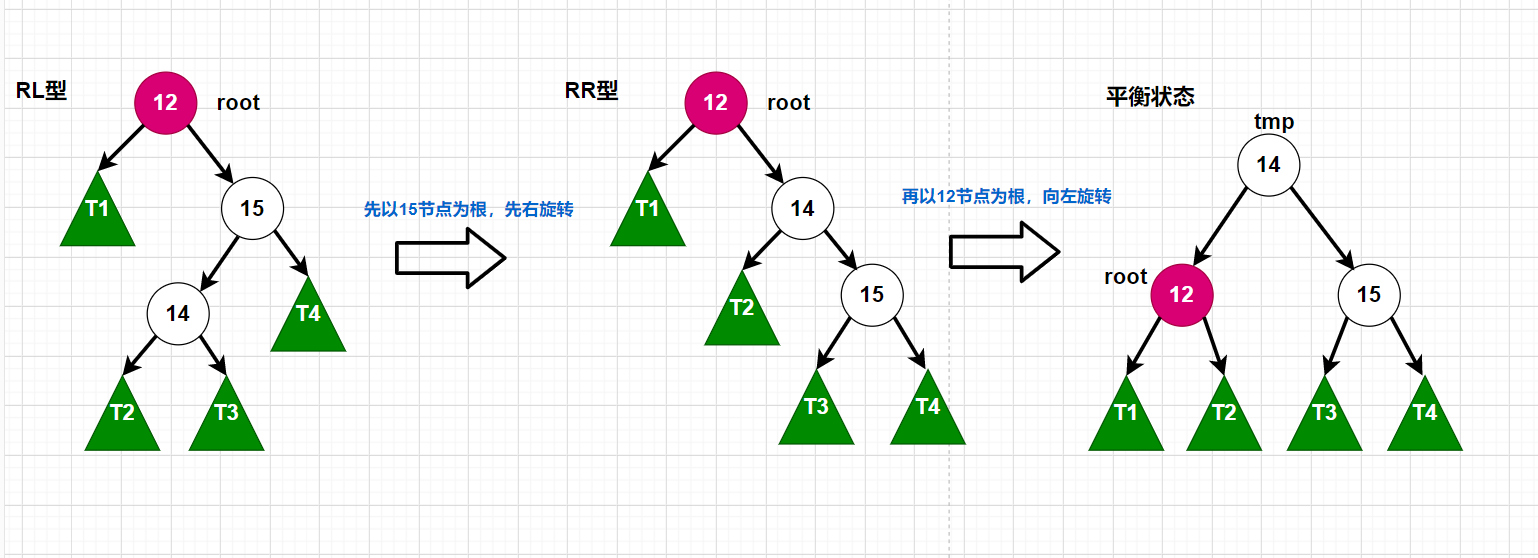
整体的代码演示,我先以图片的形式,将框架分出来,看着更为直观一点,更容易理解一点。

public void add(int val) {
root = add(root, val);
}
private TreeNode add(TreeNode node, int val) {
if (node == null) {
return new TreeNode(val);
}
if (val < node.val) {
node.left = add(node.left, val);
} else { //大于等于的情况,还是需要新建节点
node.right = add(node.right, val);
}
//计算当前节点的高度
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1; //取左右两边的最大值,再加1
//计算平衡因子
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
//LL型,做右旋转处理
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return R_Rotate(node); //直接将新的根结点返回即可
}
//RR型,做左旋转处理
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return L_Rotate(node); //新的根节点,直接返回
}
//LR型,先对左子树进行左旋转,然后再对根节点进行右旋转
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = L_Rotate(node.left); //先进行左旋转,变成LL型
return R_Rotate(node); //再进行右旋转
}
//RL型,先对右子树进行右旋转,然后再对根节点进行左旋转
node.right = R_Rotate(node.right);
return L_Rotate(node);
}
return node;
}
//计算平衡因子
private int getBalanceFactor(TreeNode node) {
if (node == null) {
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
//计算节点的高度
private int getHeight(TreeNode node) {
if (node == null) {
return 0;
}
return node.height;
}
这样的话,平衡二叉树的插入操作,我们就讲完了。接下来,我们来看看删除操作。
三、删除操作
删除和插入是一样的,我们只是在搜索二叉树的删除操作上,做一些改动,就能实现平衡二叉树的删除操作。
分析:整棵树原本是已经平衡了,是因为我们需要删除一个节点,从而导致整棵树产生不平衡。所以们只需要从删除的节点处,向上一直遍历,一直向上回溯,然后计算回溯到的节点,重新计算高度,重新计算平衡因子即可。操作完全就是add方法的一样,直接拷下来即可。下图是搜索二叉树的删除操作:

平衡二叉树的删除,简直就是一模一样。我们可以发现,在上面图中删除之后,就是直接返回了node节点,。
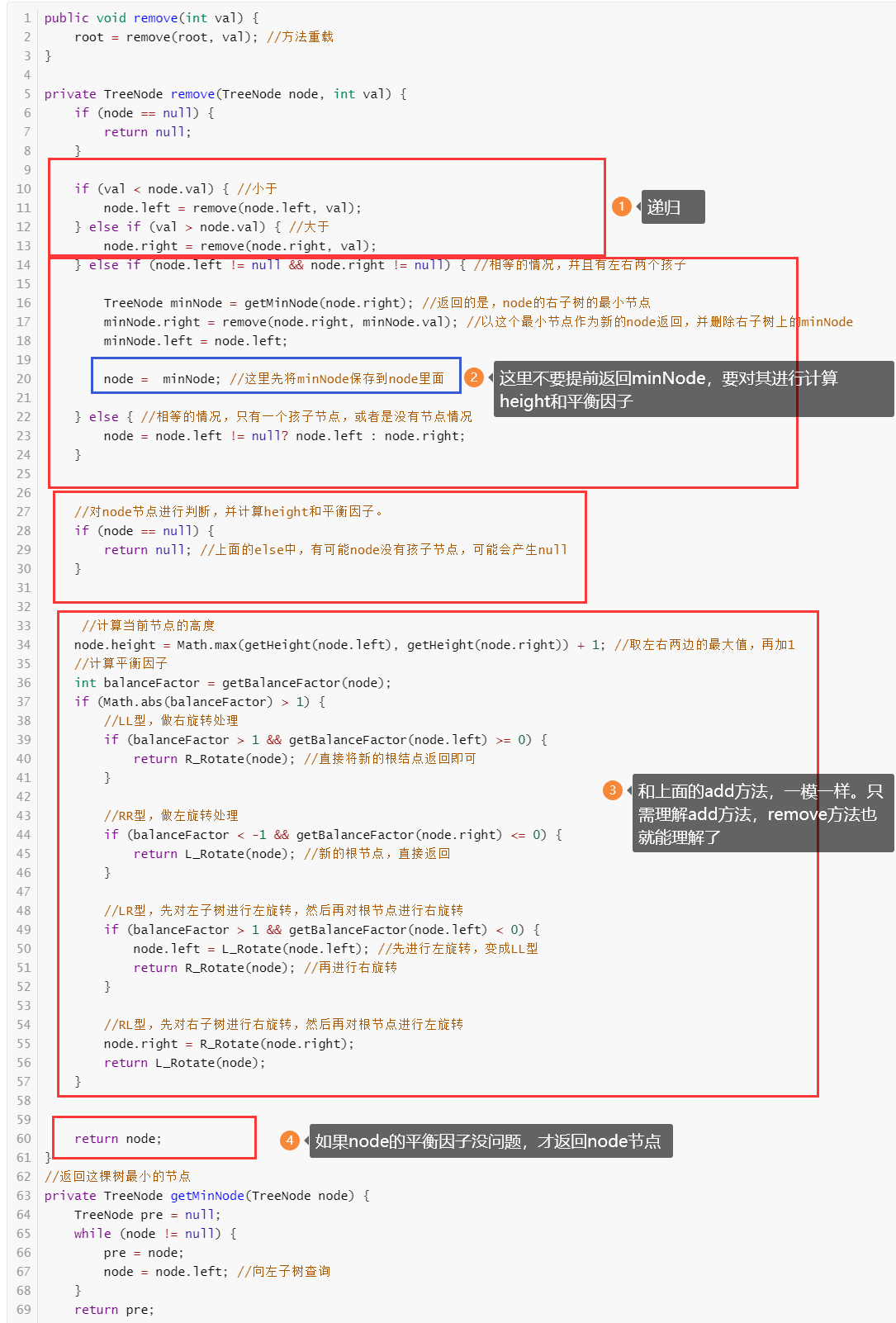
而平衡二叉树删除,就是不要先返回node节点,先对node节点进行计算height,并且计算平衡因子,如果平衡因子超过1了,就调整即可。如果平衡因子没超过1,此时 返回node节点就行。
平衡二叉树删除操作代码大致框架如下:
public void remove(int val) {
root = remove(root, val); //方法重载
}
private TreeNode remove(TreeNode node, int val) {
if (node == null) {
return null;
}
if (val < node.val) { //小于
node.left = remove(node.left, val);
} else if (val > node.val) { //大于
node.right = remove(node.right, val);
} else if (node.left != null && node.right != null) { //相等的情况,并且有左右两个孩子
TreeNode minNode = getMinNode(node.right); //返回的是,node的右子树的最小节点
minNode.right = remove(node.right, minNode.val); //以这个最小节点作为新的node返回,并删除右子树上的minNode
minNode.left = node.left;
node = minNode; //这里先将minNode保存到node里面
} else { //相等的情况,只有一个孩子节点,或者是没有节点情况
node = node.left != null? node.left : node.right;
}
//对node节点进行判断,并计算height和平衡因子。
if (node == null) {
return null; //上面的else中,有可能node没有孩子节点,可能会产生null
}
//计算当前节点的高度
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1; //取左右两边的最大值,再加1
//计算平衡因子
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
//LL型,做右旋转处理
if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
return R_Rotate(node); //直接将新的根结点返回即可
}
//RR型,做左旋转处理
if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
return L_Rotate(node); //新的根节点,直接返回
}
//LR型,先对左子树进行左旋转,然后再对根节点进行右旋转
if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
node.left = L_Rotate(node.left); //先进行左旋转,变成LL型
return R_Rotate(node); //再进行右旋转
}
//RL型,先对右子树进行右旋转,然后再对根节点进行左旋转
node.right = R_Rotate(node.right);
return L_Rotate(node);
}
return node;
}
//返回这棵树最小的节点
private TreeNode getMinNode(TreeNode node) {
TreeNode pre = null;
while (node != null) {
pre = node;
node = node.left; //向左子树查询
}
return pre;
}
对于平衡二叉树,我们只需深刻理解到LL型和RR型的旋转操作,那基本上平衡二叉树就还算掌握的不错。LR型和RL型,就是前面两种的衍生而已。不管是add方法还是remove方法;都只需在搜索二叉树的基础之上进行稍微的修改即可。最后大家可以自己再添加一下方法,例如:isBST、isBalanceTree等等。
好啦,本期更新就到此结束啦!!!同学们好好的拿出纸笔去画一画那4种旋转过程,那么恭喜你,平衡二叉树就掌握的不错啦!!!
下期见!!!