? ? ? ? ?回溯算法也是属于dfs深度优先遍历算法,普通的dfs算法只是用于可达性问题,这种问题只是需要执行到特定的位置然后返回就可以;而回溯算法主要用于求解排列组合问题,例如有{a,b,c},求解它的全排列问题,这种问题再执行到特定的位置返回之后,还会继续执行求解过程。
因为回溯算法不是立刻返回,而是继续求解,因此再程序实现的时候,需要注意对元素的标记问题:
1、再访问一个新元素进行新的递归调用的时候,需要将新元素标记为已经访问,这一才能再继续递归调用的时候,不用重复访问该元素;
2、再递归返回的时候,需要将元素标记为没有访问,因为只需要保证在一个递归链中不同时访问一个元素,可以访问以及访问过,但是不在当前递归链中的元素。

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
class Solution {
public List<String> letterCombinations(String digits) {
//开辟结果集空间
List<String> combinations = new ArrayList<>();
if(digits == null || digits.length() == 0) return combinations;
// 建立字母和数字的映射
Map<Character,String> phoneMap = new HashMap<Character,String>();
phoneMap.put('2',"abc");
phoneMap.put('3',"def");
phoneMap.put('4',"ghi");
phoneMap.put('5',"jkl");
phoneMap.put('6',"mno");
phoneMap.put('7',"pqrs");
phoneMap.put('8',"tuv");
phoneMap.put('9',"wxyz");
// 回溯算法 0 表示起始位置 ,stringbuilder是为了遍历字符串,对应结果集里面的每一个字符串组合 每次回溯index都会更新,最开始是从0开始
BackTracking(combinations,phoneMap,0,digits,new StringBuilder());
return combinations;
}
private void BackTracking(List<String> combinations,Map<Character,String> phoneMap,
int index,String digits,StringBuilder combination ){
if(index == digits.length()){ // 回溯结束的条件
combinations.add(combination.toString());
}else{ // 回溯还没结束,需要先获取当前的索引
// 获取当前是在哪个数字对应的字母上
char c = digits.charAt(index);
String leters = phoneMap.get(c);
// 获取value的长度方便后续进行遍历
int latterCount = leters.length();
for(int i =0 ;i<latterCount;i++){
// 将当前的字符串装入到stringbuild 里面
combination.append(leters.charAt(i)); // 相当于加入了a
// 进行递归 每一次递归都要向后移动一位
BackTracking(combinations,phoneMap,index+1,digits,combination);
// 回溯 相当于拼接完ad后,删除d,重新递归去寻找 ae
combination.deleteCharAt(index);
}
}
}
}
回溯+剪枝
class Solution {
public List<String> restoreIpAddresses(String s) {
// 开辟结果空间 所有可能的ip地址组合
List<String> address = new ArrayList<>();
//为每一个可能的ip地址开辟空间, 涉及到字符串的遍历StringBuilder可以直接用get遍历
StringBuilder tmpaddress = new StringBuilder();
//进行回溯算法,拼凑处所有可能的结果
// 传入的参数分别是 起始下标值、每一个可能的结果集,所有的结果、
backTracking(0,tmpaddress,address,s);
return address;
}
// 回溯算法
private void backTracking(int k ,StringBuilder tmpaddress,
List<String> address,String s ){
// 如果s的长度为0或者指针k到达了结尾位置 且又合法的4段数字ip地址
// 就进一步判断s本来就是空的情况 还是说因为遍历到了结尾后s被截取光了
// 如果是前者直接结束回溯,如果是后者则说明找到了一个满足条件的ip地址,将其添加到结果集中,然后结束本次回溯
// 特殊情况
if(s.length() == 0 || k==4){ //k==4 表示
if(s.length() == 0 && k==4){ // 访问到了结尾的位置
address.add(tmpaddress.toString());
}
// 其他情况则直接返回
return ;
}
// 普通情况 遍历所有可能的情况
for(int i =0;i<s.length() && i<=2;i++){ // 表示最大是三位数
// 如果当前s串第一个字符就是0,根据数字前置非0 原则那ip地址者一段只能是一个0,直接结束本次dfs
if(i != 0 && s.charAt(0)=='0'){
break; //结束本次循环,当前组合只能是0
}
// 找到一个片段,进一步判断其合法性
String part = s.substring(0,i+1);
if(Integer.valueOf(part)<=255){ // 小于才合法
if(tmpaddress.length() != 0){
part = '.' + part; //不是第一段
}
tmpaddress.append(part);
backTracking(k+1,tmpaddress,address,s.substring(i+1)); // 递归
// 两个参数,分别别是起始和结束位置
tmpaddress.delete(tmpaddress.length()-part.length(),tmpaddress.length());
// substring 第一个参数是起始位置,第二个参数是截取的长度
}
}
}
}
class Solution {
// 回溯算法的模板
private final static int[][] directions = {{-1,0},{0,1},{1,0},{0,-1}};
// 遍历图,需要把行总数和列总数初始化
private int row,col ;
public boolean exist(char[][] board, String word) {
row = board.length;
col = board[0].length;
boolean[][] hasVisited = new boolean[row][col];
// i++ 要先开辟一个空间然后自增,++i是再原地进行一个自增
for(int i = 0;i<row;++i){
for(int j = 0;j<col ;++j){
if(backTracking(0,i,j,hasVisited,board,word)){
return true;
}
}
}
return false;
}
// 其中r c 表示当前图中的位置,curlen为在word中的一个指针
private boolean backTracking(int curlen,int r ,int c,boolean[][] hasVisited,char[][] board,String word){
if(curlen == word.length()){
return true;
}
// dfs常规的越界条件 或者当前位置不等于,或者已经访问过,就终止回溯
if(r<0 || r>= row || c<0 || c>=col || board[r][c] != word.charAt(curlen) || hasVisited[r][c]){
return false;
}
hasVisited[r][c] = true;
for(int[] d :directions){ // 递归每个方向
if(backTracking(curlen+1,r+d[0],c+d[1],hasVisited,board,word)){ // 只有当前是true,才有下一步
return true;
}
}
// 当前者一趟dfs没有完全匹配,回溯到上一个节点,并把当前不合适的节点还原成未访问的状态
hasVisited[r][c] = false; //不满足进行回溯之前,需要先将这个位置的元素还原
return false;
}
}257、 二叉树的所有路径?https://leetcode-cn.com/problems/binary-tree-paths/

class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new ArrayList<>();
if(root == null){ // 说明传入的根节点是空
return paths;
}
List<Integer> values = new ArrayList<>(); // 保存每一趟需要的结果
backTracking(root,values,paths); //values 是每一个完整路径 即每一个子结果集
return paths;
}
private void backTracking(TreeNode node,List<Integer> values,List<String> paths){
if(node == null){ // dfs算法触底了 也是递归的返回条件
return ;
}
values.add(node.val); // 将当前节点的值加入
if(isleaf(node)){ // 如果是叶子节点,就将当前结果加入进去
paths.add(buildPath(values)); // 将满足values改为满足条件的字符串格式
}else{
// 不是叶子节点就递归左子树和右子树
backTracking(node.left,values,paths);
backTracking(node.right,values,paths);
}
//回溯部分 每次回去一个节点
values.remove(values.size()-1);
}
// 封装一个方法,判断是否为叶子节点
private boolean isleaf(TreeNode node){
return node.left== null && node.right==null;
}
private String buildPath(List<Integer> values){
// 将value进行拼接 字符串的拼接就是用stringbuild
StringBuilder sb = new StringBuilder();
for(int i =0;i<values.size();++i) {
sb.append(values.get(i));
if(i!=values.size()-1){ // 不是结尾才需要加箭头
sb.append("->");
}
}
return sb.toString();
}
}
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> permuteResult = new ArrayList<>();
List<Integer> tmpResult = new ArrayList<>();
boolean[] hasVisited = new boolean[nums.length]; // 标记访问过多元素
backtracking(nums,hasVisited,permuteResult,tmpResult);// 进行回溯
return permuteResult;
}
private void backtracking(int[] nums,boolean[] hasVisited,List<List<Integer>> permuteResult,List<Integer> tmpResult){
if(tmpResult.size() == nums.length){ // 找到一个结果集,添加进去
// 需要重构一个list,不然无法加入
permuteResult.add(new ArrayList<>(tmpResult));
return ;// 结束当前遍历
}
for(int i =0;i<nums.length;++i){
if(hasVisited[i]){
continue;
}
hasVisited[i] = true;
tmpResult.add(nums[i]);// 没访问过就加入
backtracking(nums,hasVisited,permuteResult,tmpResult);
// 回溯
tmpResult.remove(tmpResult.size()-1);
hasVisited[i] = false;
}
}
}
?
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
// 返回所有不重复的全排列 通过hashset来暴力去重
Set<List<Integer>> permuteUniqueSet = new HashSet<>();
// 每一个子结果集
List<Integer> tmplist = new ArrayList<>();
boolean[] hasVisited = new boolean[nums.length];
backTracking(nums,hasVisited,permuteUniqueSet,tmplist);
List<List<Integer>> permuteUniqueResult = new ArrayList<>(permuteUniqueSet);
return permuteUniqueResult;
}
private void backTracking(int[] nums,boolean[] hasVisited,Set<List<Integer>> permuteUniqueSet,List<Integer> tmplist){
// 判断是否到达结尾
if(tmplist.size() == nums.length){
permuteUniqueSet.add(new ArrayList<>(tmplist));
return ;
}
for(int i =0;i<hasVisited.length;++i){
if(hasVisited[i]){
continue;
}
// 没有访问过,就将这个结果加入到子结果集中
hasVisited[i] = true;
tmplist.add(nums[i]);
// 加入完成之后进行递归
backTracking(nums,hasVisited,permuteUniqueSet,tmplist);
//递归完成之后需要进行回溯 ,因为当子结果集符合要求后,已经将它加入到结果集汇总
// 故可以在这个基础上删除一个回溯,然后进行下一次递归
tmplist.remove(tmplist.size()-1);
hasVisited[i] = false;
}
}
}
class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> combineResult = new ArrayList<>();
List<Integer> tmpResult = new ArrayList<>();
backTracting(1,k,n,combineResult,tmpResult);
return combineResult;
}
private void backTracting(int start,int k,int n , List<List<Integer>> combineResult,List<Integer> tmpResult){
if(k==0){ // k 用来计数,每次-1,0表示本次结果可以先存起来
combineResult.add(new ArrayList(tmpResult)); // 因为list是一个接口,需要通过实现类来加入
return ;
}
for(int i =start;i<=n-k+1;++i) { // n-k+1 n=4,k=2 n-k+1 =3 表示取了一个数还剩下3个可以遍历
tmpResult.add(i); // 每找到一个数就加入
backTracting(i+1,k-1,n,combineResult,tmpResult) ;// i+1 表示每次往后移动一个数
// 为了保证n-k+1 不变,i+1之后k需要减一
tmpResult.remove(tmpResult.size()-1); // 回溯
}
}
}?
?
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
// 回溯算法
List<List<Integer>> combinationSumResult = new ArrayList<>();
List<Integer> tmpResult = new ArrayList<>();
backTracking(0,combinationSumResult,tmpResult,candidates,target);
return combinationSumResult;
}
private void backTracking(int start,List<List<Integer>> com,List<Integer> tmp,int[] candidates,int target){
if(target==0){ // 用target自减
com.add(new ArrayList<>(tmp));
return ;
}
for(int i =start;i< candidates.length;++i){
if(candidates[i] <= target){
tmp.add(candidates[i]);
backTracking(i,com,tmp,candidates,target-candidates[i]);//每找完一次,target要减去1,然后下一次目标值变成新的;
tmp.remove(tmp.size()-1); // 回溯
}
}
}
}?
?
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// 回溯
List<List<Integer>> comResult=new ArrayList<>();
List<Integer> tmpResult = new ArrayList<>();
boolean[] hasVisited = new boolean[candidates.length];
Arrays.sort(candidates); // 排序才好比较相邻元素是否相同
// 表示指针每次从哪开始
backTracking(0,hasVisited,comResult,tmpResult,candidates,target);
return comResult;
}
private void backTracking(int start,boolean[] hasVisited,List<List<Integer>> comResult,List<Integer> tmpResult,int[] candidates, int target){
// 对target原地做减法操作
if(target == 0){
comResult.add(new ArrayList<>(tmpResult));
return ;
}
for(int i =start;i<candidates.length;++i){
// 重复且没访问过的,跳出
if(i!=0 && candidates[i] == candidates[i-1] && !hasVisited[i-1]){
continue;
}
if(candidates[i] <= target){
hasVisited[i] = true;
tmpResult.add(candidates[i]);
// 记得更新target
backTracking(i+1,hasVisited,comResult,tmpResult,candidates,target-candidates[i]);
tmpResult.remove(tmpResult.size()-1);
hasVisited[i] = false;
}
}
}
}?
class Solution {
public List<List<Integer>> combinationSum3(int k, int n) {
List<List<Integer>> combinationSumResult = new ArrayList<>();
List<Integer> tmpResult = new ArrayList<>();
//开始下标,由于是正整数所以从1开始
backTracking(1,k,n,combinationSumResult,tmpResult);
return combinationSumResult;
}
private void backTracking(int start,int k,int n,List<List<Integer>> combination,List<Integer> tmpResult ){
if(k==0 && n==0){ // 原地自减,n=0 表示和刚好为0
combination.add(new ArrayList<>(tmpResult));
return ;
}
//不满足的情况,k减少到0 但是n不等于0,就结束不次dfs
if(k==0 && n!= 0){
return ;
}
for(int i = start;i<=9;++i){
tmpResult.add(i); // 满足条件直接加入
backTracking(i+1,k-1,n-i,combination,tmpResult); // 递归,其实位置后移,个数需要减去1,综合减去i
tmpResult.remove(tmpResult.size()-1);
}
}
}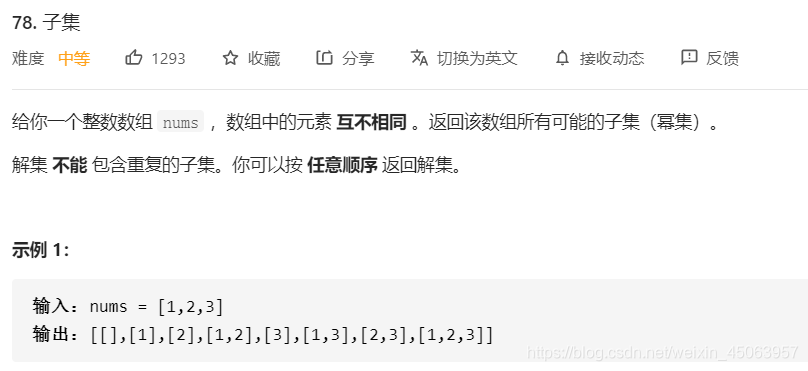
class Solution {
// 递归,回溯算法
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> allSubSets = new ArrayList<>();
List<Integer> tempSubset = new ArrayList<>();
for(int size = 0;size<=nums.length;size++){
// 所有子集的长度可能为0~nums.length,每一个可能长度size我们都要dfs
// 并且回溯它所有可能的排列组合
// 回溯算法
backTracking(0,size,nums,tempSubset,allSubSets);
}
return allSubSets;
}
// 回溯算法 起始位置,子数组大小
private void backTracking(int start,int size,int[] nums,List<Integer> temp,
List<List<Integer>> allSubSets){
if(temp.size() == size){ //大小相同,递归完成
allSubSets.add(new ArrayList<>(temp));
return ;
}
for(int i=start;i<nums.length;i++){
temp.add(nums[i]);
backTracking(i+1,size,nums,temp,allSubSets); // 递归
temp.remove(temp.size()-1); // 回溯
}
}
}
?
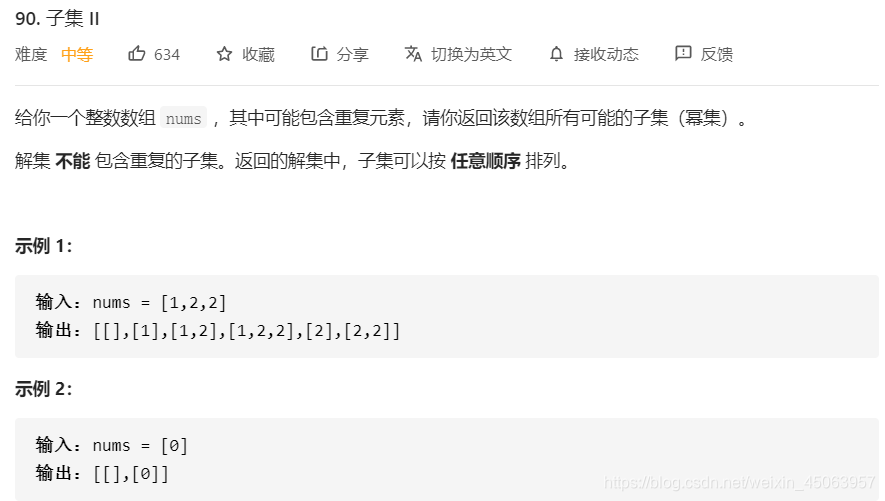
class Solution {
public List<List<Integer>> subsetsWithDup(int[] nums) {
List<List<Integer>> subsetsWithDup = new ArrayList<>();
List<Integer> subsetList = new ArrayList<>();
boolean[] hasvisited = new boolean[nums.length] ;
Arrays.sort(nums);
// 每种长度的子集都有多种组合
for(int size =0;size<=nums.length;size++){
// 回溯
backTracking(0,size,hasvisited,subsetList,subsetsWithDup,nums);
}
return subsetsWithDup;
}
private void backTracking(int start,
int size,
boolean[] hasvisited,
List<Integer> subsetlist,
List<List<Integer>> subsetsWithDup,
int[] nums ){
// 满足条件就将这个数组加进去
if(subsetlist.size()==size){
subsetsWithDup.add(new ArrayList<>(subsetlist));
return ;
}
for(int i =start;i<nums.length;i++){
// 手动去重 还要是没有访问过的位置
if(i !=0 && nums[i] ==nums[i-1] && !hasvisited[i-1]){
continue;
}
hasvisited[i] = true; // 表示已经访问过了
subsetlist.add(nums[i]); // 将这个元素加入
// 递归
backTracking(i+1,size,hasvisited,
subsetlist,subsetsWithDup,nums);
// 回溯往回退一步
subsetlist.remove(subsetlist.size()-1);
hasvisited[i] =false; // 回退之后还原状态为没有访问过
}
}
}