1、String原理及实现
string类是由模板类basic_string<class _CharT,class _traits,class _alloc>实例化生成的一个类。basic_tring是由_String_base继承而来的。
typedef basic_string<char> string而实际面试由于时间关系,一般不会要求很详细的string的功能,一般要求是实现构造函数,拷贝构造函数,赋值函数,析构函数等部分,因为string里面涉及动态内存管理,默认的拷贝构造函数在运行只会进行浅复制,这样会造成两个对象指向一块区域内存的对象。如果一个对象被销毁,会造成另外一个对象运行出错,这时要进行深拷贝。
#pragma once
// 为了避免同一个头文件被包含(include)多次,C/C++中有两种宏实现方式:一种是#ifndef方式;
// 另一种是#pragma once方式。
#include<iostream>
class String
{
private:
char* data; //字符串内容
size_t length; //字符串长度
public:
String(const char* str = nullptr); //通用构造函数
String(const String& str); //拷贝构造函数
~String(); //析构函数
// const类似于java的static final
String operator+(const String &str) const; //重载+
String& operator=(const String &str); //重载=
String& operator+=(const String &str); //重载+=
bool operator==(const String &str) const; //重载==
friend std::istream& operator>>(std::istream &is, String &str);//重载>>
friend std::ostream& operator<<(std::ostream &os, String &str);//重载<<
char& operator[](int n)const; //重载[]
size_t size() const; //获取长度
const char* c_str() const; //获取C字符串
};#include"String.h"
//通用构造函数
String::String(const char *str)
{
if (!str)
{
length = 0;
data = new char[1]; //一定要用new分配内存,否则就变成了浅拷贝;
*data = '\0';
}
else
{
length = strlen(str); //
data = new char[length + 1];
strcpy(data,str);
}
}
//拷贝构造函数
String::String(const String& str)
{
length = str.size();
data = new char[length + 1]; //一定要用new,否则变成了浅拷贝
strcpy(data,str.c_str());
}
//析构函数
String::~String()
{
delete[]data;
length = 0;
}
//重载+
String String::operator+(const String &str) const
{
String StringNew;
StringNew.length = length + str.size();
StringNew = new char[length + 1];
strcpy(StringNew.data, data);
strcat(StringNew.data, str.data); //字符串拼接函数,即将str内容复制到StringNew内容后面
return StringNew;
}
//重载=
String& String::operator=(const String &str)
{
if (this == &str)
{
return *this;
}
delete []data; //释放内存
length = str.length;
data = new char[length + 1];
strcpy(data,str.c_str());
return *this;
}
//重载+=
String& String::operator+=(const String &str)
{
length += str.size();
char *dataNew = new char[length + 1];
strcpy(dataNew, data);
delete[]data;
strcat(dataNew, str.c_str());
data = dataNew;
return *this;
}
//重载==
bool String::operator==(const String &str) const
{
if (length != str.length)
{
return false;
}
return strcmp(data, str.data) ? false : true;
}
//重载[]
char& String::operator[](int n) const //str[n]表示第n+1个元素
{
if (n >= length)
{
return data[length - 1]; //错误处理
}
else
{
return data[n];
}
}
//获取长度
size_t String::size() const
{
return this->length;
}
//获取C字符串
const char* String::c_str() const
{
return data;
}
//重载>>
std::istream& operator>>(std::istream &is, String &str)
{
char tem[1000];
is >> tem;
str.length = strlen(tem);
str.data = new char[str.length + 1];
strcpy(str.data, tem);
return is;
}
//重载<<
std::ostream& operator<<(std::ostream &os, String &str)
{
os << str.c_str();
return os;
}关于operator>>和operator<<运算符重载,我们是设计成友元函数(非成员函数),并没有设计成成员函数。
原因如下:对于一般的运算符重载都设计为类的成员函数,而>>和<<却不这样设计,因为作为一个成员函数,其左侧操作数必须是隶属同一个类之下的对象,如果设计成员函数,输出为 对象>>cout >> endl;(Essential C++)不符合习惯。
一般情况下:
- 将双目运算符重载为友元函数,这样就可以使用交换律,比较方便
- 单目运算符一般重载为成员函数,因为直接对类对象本身进行操作
- 运算符重载函数可以作为成员函数,友元函数,普通函数。
- 普通函数:一般不用,通过类的公共接口间接访问私有成员。
- 成员函数:可通过this指针访问本类的成员,可以少写一个参数,但是表达式左边的第一个参数必须是类对象,通过该类对象来调用成员函数。
- 友元函数:左边一般不是对象。<< >>运算符一般都要申明为友元重载函数
2、链表的实现
2.1、顺序链表
最简单的数据结构,开辟一块连续的存储空间,用数组实现。
#pragma once
#ifndef SQLIST_H
#define SQLIST_H
#define MaxSize 50
typedef int DataType;
struct SqList //顺序表相当于一个数组,这个结构体就已经表示了整个顺序表
{
DataType data[MaxSize];
int length; //表示顺序表实际长度
};//顺序表类型定义
void InitSqList(SqList * &L);
//释放顺序表
void DestroySqList(SqList * L);
//判断是否为空表
int isSqListEmpty(SqList * L);
//返回顺序表的实际长度
int SqListLength(SqList * L);
//获取顺序表中第i个元素值
DataType SqListGetElem(SqList * L, int i);
//在顺序表中查找元素e,并返回在顺序表哪个位置
int GetElemLocate(SqList * L, const DataType e);
//在第i个位置插入元素
int SqListInsert(SqList *&L, int i, DataType e);
//删除第i个位置元素,并返回该元素的值
DataType SqListElem(SqList* L, int i);
#endif#include<iostream>
#include"SqList.h"
using namespace std;
//初始化顺序表
void InitSqList(SqList * &L)
{
L = (SqList*)malloc(sizeof(SqList)); // 开辟内存
L->length = 0;
}
//释放顺序表
void DestroySqList(SqList * L)
{
if (L == NULL)
{
return;
}
free(L);
}
//判断是否为空表
int isSqListEmpty(SqList * L)
{
if (L == NULL)
{
return 0;
}
return (L->length == 0);
}
//返回顺序表的实际长度
int SqListLength(SqList * L)
{
if (L == NULL)
{
cout << "顺序表分配内存失败" << endl;
return 0;
}
return L->length;
}
//获取顺序表中第i个元素值
DataType SqListGetElem(SqList * L,int i)
{
if (L == NULL)
{
cout << "No Data in SqList" << endl;
return 0;
}
return L->data[i - 1];
}
//在顺序表中查找元素e,并返回在顺序表哪个位置
int GetElemLocate(SqList * L, const DataType e)
{
if( L == NULL)
{
cout << "Empty SqList" << endl;
return 0;
}
int i = 0;
while(i < L->length && L->data[i] != e)
{
i++;
}
if (i > L->length)
return 0;
return i + 1;
}
//在第i个位置插入元素
int SqListInsert(SqList *&L, int i, DataType e)
{
if(L == NULL)
{
cout << "error" << endl;
return 0;
}
if (i > L->length + 1 || i < 1)
{
cout << "error" << endl;
return 0;
}
for (int j = L->length; j>=i - 1; j--) //将i之后的元素后移,腾出空间
{
L->data[j] = L->data[j - 1];
}
L->data[i] = e;
L->length++;
return 1;
}
//删除第i个位置元素,并返回该元素的值
DataType SqListElem(SqList* L, int i)
{
if (L == NULL)
{
cout << "error" << endl;
return 0;
}
if (i < 0 || i > L->length)
{
cout << "error" << endl;
return 0;
}
DataType e = L->data[i - 1];
for (int j = i; j < L->length;j++)
{
L->data[j] = L->data[j + 1];
}
L->length--;
return e;
}2.2、链式表
#pragma once
#ifndef LINKLIST_H
#define LINKLIST_H
typedef int DataType;
//单链表:单链表是一个节点一个节点构成,
//先定义一个节点,节点为一个结构体,当这些节点连在一起,
// 链表为指向头结点的结构体型指针,即是LinkList型指针
typedef struct LNode //定义的是节点的类型
{
DataType data;
struct LNode *next; //指向后继节点
}LinkList;
void InitLinkList(LinkList * &L); //初始化链表
void DestroyLinkList(LinkList * L); //销毁单链表
int isEmptyLinkList(LinkList * L); //判断链表是否为空
int LinkListLength(LinkList * L); //求链表长度
void DisplayLinkList(LinkList * L); //输出链表元素
DataType LinkListGetElem(LinkList * L,int i);//获取第i个位置的元素值
int LinkListLocate(LinkList * L,DataType e); //元素e在链表的位置
int LinkListInsert(LinkList * &L,int i,DataType e);//在第i处插入元素e
DataType LinkListDelete(LinkList * &L,int i); //删除链表第i处的元素
#endif#include<iostream>
#include"LinkList.h"
using namespace std;
void InitLinkList(LinkList * &L) //初始化链表
{
L = (LinkList*)malloc(sizeof(LinkList)); //创建头结点
L->next = NULL;
}
void DestroyLinkList(LinkList * L) //销毁单链表
{
LinkList *p = L, *q = p->next;//创建辅助节点指针
if(L == NULL)
{
return;
}
while (q != NULL) //销毁一个链表,必须一个节点一个节点的销毁
{
free(p);
p = q;
q = p->next;
}
free(p);
}
int isEmptyLinkList(LinkList * L) //判断链表是否为空
{
return (L->next == NULL);// 1:空;0:非空
}
int LinkListLength(LinkList * L) //求链表长度,链表的长度必须一个节点一个节点的遍历
{
LinkList *p = L;
if (L == NULL)
{
return 0;
}
int i = 0;
while (p->next != NULL)
{
i++;
p = p->next;
}
return i;
}
void DisplayLinkList(LinkList * L)//输出链表元素
{
LinkList * p = L->next; //此处一点要指向next,这样是第一个节点,跳过了头结点
while (p != NULL)
{
cout << p->data << " ";
p = p->next;
}
cout << endl;
}
DataType LinkListGetElem(LinkList * L, int i)//获取第i个位置的元素值
{
LinkList *p = L;
if (L == NULL || i < 0)
{
return 0;
}
int j = 0;
while (j < i && p->next != NULL)
{
j++; p = p->next;
}
if (p == NULL)
{
return 0;
}
else
{
return p->data;
}
}
int LinkListLocate(LinkList * L, DataType e) //元素e在链表的位置
{
LinkList *p = L;
if (L == NULL)
{
return 0;
}
int j = 0;
while (p->next != NULL && p->data == e)
{
j++;
}
return j+1;
}
int LinkListInsert(LinkList * &L, int i, DataType e)//在第i处插入元素e
{
LinkList *p = L,*s;
int j = 0;
if (L == NULL )
{
return 0;
}
while (j < i-1 && p != NULL) //先将指针移到该处
{
j++;
p = p->next;
}
s = (LinkList*)malloc(sizeof(LinkList)); //添加一个节点,需开辟一个新的内存
s->data = e;
s->next = p->next; //先将下一地址给新节点
p->next = s; //将原来的指针指向新节点
return 1;
}
DataType LinkListDelete(LinkList * &L, int i) //删除链表第i处的元素
{
LinkList *p = L,*q; //p用来存储临时节点
DataType e; //用来存被删除点的元素
int j = 0;
while (j < i - 1 && p != NULL) //将p指向第i-1节点
{
j++;
p = p->next;
}
if (p == NULL)
{
return 0;
}
else
{
q = p->next; //q指向第i个节点*p
e = q->data; //
p->next = q->next;//从链表中删除p节点,即是p->next = p->next->next,将第i个节点信息提取出来
free(q); //释放p点内存
return e;
}
}2.3、双链表
#pragma once
#ifndef DLINKLIST_H
#define DLINKLIST_H
typedef int DataType;
typedef struct DLNode
{
DataType Elem;
DLNode *prior;
DLNode *next;
}DLinkList;
void DLinkListInit(DLinkList *&L);//初始化双链表
void DLinkListDestroy(DLinkList * L); //双链表销毁
bool isDLinkListEmpty(DLinkList * L);//判断链表是否为空
int DLinkListLength(DLinkList * L); //求双链表的长度
void DLinkListDisplay(DLinkList * L); //输出双链表
DataType DLinkListGetElem(DLinkList * L, int i); //获取第i个位置的元素
bool DLinkListInsert(DLinkList * &L, int i, DataType e);//在第i个位置插入元素e
DataType DLinkListDelete(DLinkList * &L, int i);//删除第i个位置上的值,并返回其值
#endif#include<iostream>
#include"DLinkList.h"
using namespace std;
void DLinkListInit(DLinkList *&L)//初始化双链表
{
L = (DLinkList *)malloc(sizeof(DLinkList)); //创建头结点
L->prior = L->next = NULL;
}
void DLinkListDestroy(DLinkList * L) //双链表销毁
{
if (L == NULL)
{
return;
}
DLinkList *p = L, *q = p->next;//定义两个节点,第一个表示当前节点,第二个表示第二个节点
while (q != NULL) //当第二个节点指向null,说明p是最后一个节点,如果不是,则
{ //释放掉p,q就为第一个节点,将q赋给p,p->给q,这样迭代
free(p);
p = q;
q = p->next;
}
free(p);
}
bool isDLinkListEmpty(DLinkList * L)//判断链表是否为空
{
return L->next == NULL;
}
int DLinkListLength(DLinkList * L) //求双链表的长度
{
DLinkList *p = L;
if (L == NULL)
{
return 0;
}
int i = 0;
while (p->next != NULL)
{
i++;
p = p->next;
}
return i;
}
void DLinkListDisplay(DLinkList * L) //输出双链表
{
DLinkList *p = L->next; //跳过头结点,指向第一个节点
while (p != NULL)
{
cout << p->Elem << " ";
p = p->next;
}
}
DataType DLinkListGetElem(DLinkList * L, int i) //获取第i个位置的元素
{
DLinkList *p = L;//指向头结点
if (L == NULL)
{
cout << "Function DLinkListGetElem" << "链表为空表" << endl;
return 0;
}
int j = 0;
while (p != NULL && j < i) //将指针指向第i个位置处
{
j++;
p = p->next;
}
if (p == NULL)
{
return 0;
}
else
{
return p->Elem;
}
}
bool DLinkListInsert(DLinkList * &L, int i, DataType e)//在第i个位置插入元素e
{
int j = 0;
DLinkList *p = L, *s;//其中s节点是表示插入的那个节点,所以要给它开辟内存
while (p != NULL && j < i - 1) //插入节点前,先找到第i-1个节点
{
j++;
p = p->next;
}
if( p == NULL)
{
return 0;
}
else
{
s = (DLinkList *)malloc(sizeof(DLinkList));
s->Elem = e;
s->next = p->next;//插入点后继的指向
if (p->next != NULL)
{
p->next->prior = s; //插入点的后继的前驱指向
}
s->prior = p; //插入点前驱的前驱指向
p->next = s; //插入点后前驱的后继指向
}
}
DataType DLinkListDelete(DLinkList * &L, int i)//删除第i个位置上的值,并返回其值
{
DLinkList *p = L, *s;
int j = 0;
if (L == NULL)
{
cout << "Function DLinkListDelete" << "删除出错" << endl;
return 0;
}
while (j < i - 1 && p != NULL)
{
j++;
p = p->next;
}
if (p == NULL)
{
return 0;
}
else
{
s = p->next;
if (s == NULL)
{
return 0;
}
DataType e = p->Elem;
p->next = s->next;
if (p->next != NULL)
{
p->next->prior = p;
}
free(s);
return e;
}
}3、队列
3.1、顺序队列
#pragma once
#ifndef SQQUEUE_H
#define SQQUEUE_H
#define MaxSize 50
typedef int DataType;
typedef struct SQueue //创建一个结构体,里面包含数组和队头和队尾
{
DataType data[MaxSize];
int front, rear; //front表示队头,rear表示队尾,入队头不动尾动,出队尾不动头动
}SqQueue;
void SqQueueInit(SqQueue *&Q); //队列初始化
void SqQueueClear(SqQueue *$Q); //清空队列
bool isSqQueueEmpty(SqQueue *Q); //判断队列长度
int SqQueueLength(SqQueue *Q); //求队列的长度
void SqQueueDisplay(SqQueue *Q); //输出队列
void EnSqQueue(SqQueue *& Q,DataType e); //进队
DataType DeSqQueue(SqQueue *& Q); //出队
#endif#include<iostream>
#include"SqQueue.h"
using namespace std;
void SqQueueInit(SqQueue *&Q) //队列初始化
{
Q = (SqQueue *)malloc(sizeof(Q));
Q->front = Q->rear = 0;
}
void SqQueueClear(SqQueue *&Q) //清空队列
{
free(Q); //对于顺序栈,直接释放内存即可
}
bool isSqQueueEmpty(SqQueue *Q) //判断队列长度
{
return (Q->front == Q->rear);
}
int SqQueueLength(SqQueue *Q) //求队列的长度
{
return Q->rear - Q->front; //此处有问题
}
void EnSqQueue(SqQueue *& Q,DataType e) //进队
{
if (Q == NULL)
{
cout << "分配内存失败!" << endl;
return;
}
if (Q->rear >= MaxSize) //入队前进行队满判断
{
cout << "The Queue is Full!" << endl;
return;
}
Q->rear++;
Q->data[Q->rear] = e;
}
DataType DeSqQueue(SqQueue *& Q) //出栈
{
if (Q == NULL)
{
return 0;
}
if (Q->front == Q->rear) //出队前进行空队判断
{
cout << "This is an Empty Queue!" << endl;
return 0;
}
Q->front--;
return Q->data[Q->front];
}
void SqQueueDisplay(SqQueue *Q) //输出队列
{
if (Q == NULL)
{
return;
}
if (Q->front == Q->rear)
{
return;
}
int i = Q->front + 1;
while (i <= Q->rear)
{
cout << Q->data[i] << " ";
i++;
}
}3.2、链式队列
#pragma once
#ifndef LINKQUEUE_H
#define LINKQUEUE_H
typedef int DataType;
/*
队列的链式存储中,由于需要指针分别指向
队头和队尾,因此造成了链队节点与数据节点不同
链队节点:包含两个指向队头队尾的指针
数据节点:一个指向下一个数据节点的指针和数据
*/
//定义数据节点结构体
typedef struct qnode
{
DataType Elem;
struct qnode *next;
}QDataNode;
//定义链队节点结构体
typedef struct
{
QDataNode *front;
QDataNode *rear;
}LinkQueue;
void LinkQueueInit(LinkQueue *&LQ); //初始化链队
void LinkQueueClear(LinkQueue *&LQ); //清空链队
bool isLinkQueueEmpty(LinkQueue *LQ); //判断链队是否为空
int LinkQueueLength(LinkQueue *LQ); //求链队长度
bool EnLinkQueue(LinkQueue *&LQ,DataType e); //进队
DataType DeLinkQueue(LinkQueue *&LQ); //出队
#endif#include<iostream>
#include"LinkQueue.h"
using namespace std;
void LinkQueueInit(LinkQueue *&LQ) //初始化链队
{
LQ = (LinkQueue*)malloc(sizeof(LQ));
LQ->front = LQ->rear = NULL;
}
void LinkQueueClear(LinkQueue *&LQ) //清空链队,清空队列第一步:销毁数据节点
// 第二步:销毁链队节点
{
QDataNode *p = LQ->front, *r;
if (p != NULL)
{
r = p->next;
while (r != NULL)
{
free(p);
p = r;
r = p->next;
}
}
free(LQ);
}
bool isLinkQueueEmpty(LinkQueue *LQ) //判断链队是否为空
{
return LQ->rear == NULL; //1:非空;0:空
}
int LinkQueueLength(LinkQueue *LQ) //求链队长度
{
QDataNode *p = LQ->front;
int i = 0;
while (p != NULL)
{
i++;
p = p->next;
}
return i;
}
bool EnLinkQueue(LinkQueue *&LQ, DataType e) //进队
{
QDataNode *p;
if (LQ == NULL)
{
return 0;
}
p = (QDataNode*)malloc(sizeof(QDataNode));
p->Elem = e;
p->next = NULL; //尾插法
if (LQ->front == NULL)//如果队列中还没有数据时
{
LQ->front = LQ->rear = p; //p为队头也为队尾
}
else
{
LQ->rear->next = p;
LQ->rear = p;
}
}
DataType DeLinkQueue(LinkQueue *&LQ) //出队
{
QDataNode *p;
DataType e;
if (LQ->rear == NULL)
{
cout << "This is an Empty queue!" << endl;
return 0;
}
if (LQ->front == LQ->rear)
{
p = LQ->front;
LQ->rear = LQ->front = NULL;
}
else
{
p = LQ->front;
LQ->front = p->next;
e = p->Elem;
}
free(p);
return e;
}4、栈
4.1、顺序栈
#pragma once
#ifndef SQSTACK_H
#define SQSTACK_H
#define MaxSize 50//根据实际情况设置大小
typedef int DataType;
//顺序栈也是一种特殊的顺序表,创建一个
//结构体,里面包含一个数组,存储数据
//顺序栈其实是将数组进行结构体包装
typedef struct Stack
{
DataType Elem[MaxSize];
int top; //栈指针
}SqStack;
void SqStackInit(SqStack *&S); //初始化栈
void SqStackClear(SqStack *&S); //清空栈
int SqStackLength(SqStack *S); //求栈的长度
bool isSqStackEmpty(SqStack *S); //判断栈是否为空
void SqStackDisplay(SqStack *S); //输出栈元素
bool SqStackPush(SqStack *&S, DataType e);//元素e进栈
DataType SqStackPop(SqStack *&S);//出栈一个元素
DataType SqStackGetPop(SqStack *S);//取栈顶元素
#endif#include<iostream>
#include"SqStack.h"
using namespace std;
void SqStackInit(SqStack *&S) //初始化栈
{
S = (SqStack*)malloc(sizeof(SqStack)); //开辟内存,创建栈
S->top = -1;
}
void SqStackClear(SqStack *&S) //清空栈
{
free(S);
}
int SqStackLength(SqStack *S) //求栈的长度
{
return S->top + 1;
}
bool isSqStackEmpty(SqStack *S) //判断栈是否为空
{
return (S->top == -1);
}
void SqStackDisplay(SqStack *S) //输出栈元素
{
for (int i = S->top; i > -1; i--)
{
cout << S->Elem[i] << " ";
}
}
bool SqStackPush(SqStack *&S, DataType e)//元素e进栈
{
if ( S->top == MaxSize - 1)
{
cout << "The Stack Full!" << endl; //满栈判断
return 0;
}
S->top++;
S->Elem[S->top] = e;
return 1;
}
DataType SqStackPop(SqStack *&S)//出栈一个元素
{
DataType e;
if(S->top== -1) //空栈判断
{
cout << "The Stack is Empty!" << endl;
return 0;
}
e = S->Elem[S->top];//出栈元素存储
S->top--;
return e;
}
DataType SqStackGetPop(SqStack *S)//取栈顶元素
{
if (S->top == -1) //空栈判断
{
cout << "The Stack is Empty" << endl;
return 0;
}
return S->Elem[S->top];
}4.2、链式栈
#pragma once
#ifndef LINKSTACK_H
#define LINKSTACK_H
typedef int DataType;
typedef struct LinkNode //链式栈的结点定义和链表的结点定义是一样的
{
DataType Elem; //数据域
struct LinkNode *next; //指针域
}LinkStack;
void LinkStackInit(LinkStack *& S); //初始化列表
void LinkStackClear(LinkStack*&S); //清空栈
int LinkStackLength(LinkStack * S); //求链表的长度
bool isLinkStackEmpty(LinkStack *S); //判断链表是否为空
bool LinkStackPush(LinkStack *S, DataType e);//元素e进栈
DataType LinkStackPop(LinkStack *S); //出栈
DataType LinkStackGetPop(LinkStack *S); //输出栈顶元素
void LinkStackDisplay(LinkStack *S); //从上到下输出栈所有元素
#endif#include<iostream>
#include"LinkStack.h"
using namespace std;
void LinkStackInit(LinkStack *& S) //初始化列表
{
S = (LinkStack *)malloc(sizeof(LinkStack)); //分配内存
S->next = NULL;
}
void LinkStackClear(LinkStack*&S) //清空栈
{
LinkStack *p = S,*q = S->next;
if (S == NULL)
{
return;
}
while (p != NULL) //注意:与书中有点不同,定义两个节点,一个当前节点,一个下一个节点
{
free(p);
p = q;
q = p->next;
}
}
int LinkStackLength(LinkStack * S)//求链表的长度
{
int i = 0;
LinkStack *p = S->next; //跳过头结点
while (p != NULL)
{
i++;
p = p->next;
}
return i;
}
bool isLinkStackEmpty(LinkStack *S)//判断链表是否为空
{
return S->next == NULL; //1:空;0:非空
}
bool LinkStackPush(LinkStack *S, DataType e)//元素e进栈
{
LinkStack *p;
p = (LinkStack*)malloc(sizeof(LinkStack)); //创建结点
if (p == NULL)
{
return 0;
}
p->Elem = e; //将元素赋值
p->next = S->next; //将新建结点的p->next指向原来的栈顶元素
S->next = p; //将现在栈的起始点指向新建结点
return 1;
}
DataType LinkStackPop(LinkStack *S)//出栈
{
LinkStack *p;
DataType e;
if (S->next == NULL)
{
cout << "The Stack is Empty!" << endl;
return 0;
}
p = S->next; //跳过头结点
e = p->Elem;
S->next = p->next;
return e;
}
DataType LinkStackGetPop(LinkStack *S)//输出栈顶元素
{
if (S->next == NULL)
{
cout << "The Stack is Empty!" << endl;
return 0;
}
return S->next->Elem; //头结点
}
void LinkStackDisplay(LinkStack *S)//从上到下输出栈所有元素
{
LinkStack *p = S->next;
while(p != NULL)
{
cout << p->Elem << " ";
p = p->next;
}
cout << endl;
}5、二叉树
5.1、二叉树的链式存储
#pragma once
#ifndef LINKBTREE_H
#define LINKBTREE_H
#define MaxSize 100 //树的深度
typedef char DataType;
typedef struct BTNode //定义一个二叉树节点
{
DataType Elem;
BTNode *Lchild;
BTNode *Rchild;
}LinkBTree;
void LinkBTreeCreate(LinkBTree *& BT, char *str);//有str创建二叉链
LinkBTree* LinkBTreeFindNode(LinkBTree * BT, DataType e); //返回e的指针
LinkBTree *LinkBTreeLchild(LinkBTree *p);//返回*p节点的左孩子节点指针
LinkBTree* LinkBTreeRight(LinkBTree *p);//返回*p节点的右孩子节点指针
int LinkBTreeDepth(LinkBTree *BT);//求二叉链的深度
void LinkBTreeDisplay(LinkBTree * BT);//以括号法输出二叉链
int LinkBTreeWidth(LinkBTree *BT);//求二叉链的宽度
int LinkBTreeNodes(LinkBTree * BT);//求节点个数
int LinkBTreeLeafNodes(LinkBTree *BT);//求二叉链的叶子节点个数
void LinkBTreeProOeder(LinkBTree *BT); //前序递归遍历
void LinkBTreeProOederRecursion(LinkBTree *BT);//前序非递归遍历
void LinkBTreeInOeder(LinkBTree *BT);//中序递归遍历
void LinkBTreeInOederRecursion(LinkBTree *BT);//中序非递归遍历
void LinkBTreePostOeder(LinkBTree *BT);//后序递归遍历
void LinkBTreePostOederRecursion(LinkBTree *BT);//后序非递归遍历
#endif#include<iostream>
#include"LinkBTree.h"
using namespace std;
void LinkBTreeCreate(LinkBTree *& BT, char *str)//有str创建二叉链
{
LinkBTree *St[MaxSize], *p = NULL;
int top = -1, k, j = 0;
char ch;
BT = NULL;
ch = str[j];
while (ch != '\0')
{
switch (ch)
{
case '(':top++; St[top] = p; k = 1; break;//为左节点,top表示层数,k表示左右节点,碰到一个'('二叉树加一层,碰到一个',',变成右子树
case ')':top--; break;
case ',':k = 2; break; //为右节点
default: p = (LinkBTree *)malloc(sizeof(LinkBTree));
p->Elem = ch;
p->Lchild = p->Rchild = NULL;
if (BT == NULL)
{
BT = p; //根节点
}
else
{
switch (k)
{
case 1:St[top]->Lchild = p; break;
case 2:St[top]->Rchild = p; break;
}
}
}
j++;
ch = str[j];
}
}
LinkBTree *LinkBTreeFindNode(LinkBTree * BT, DataType e) //返回元素e的指针
{
LinkBTree *p;
if (BT == NULL)
{
return NULL;
}
else if (BT->Elem == e)
{
return BT;
}
else
{
p = LinkBTreeFindNode(BT->Lchild, e); //递归
if (p != NULL)
{
return p;
}
else
{
return LinkBTreeFindNode(BT->Lchild, e);
}
}
}
LinkBTree *LinkBTreeLchild(LinkBTree *p)//返回*p节点的左孩子节点指针
{
return p->Lchild;
}
LinkBTree *LinkBTreeRight(LinkBTree *p)//返回*p节点的右孩子节点指针{
{
return p->Rchild;
}
int LinkBTreeDepth(LinkBTree *BT)//求二叉链的深度
{
int LchildDep, RchildDep;
if (BT == NULL)
{
return 0;
}
else
{
LchildDep = LinkBTreeDepth(BT->Lchild);
RchildDep = LinkBTreeDepth(BT->Rchild);
}
return (LchildDep > RchildDep) ? (LchildDep + 1) : (RchildDep + 1);
}
void LinkBTreeDisplay(LinkBTree * BT)//以括号法输出二叉链
{
if (BT != NULL)
{
cout << BT->Elem;
if (BT->Lchild != NULL || BT->Rchild != NULL)
{
cout << '(';
LinkBTreeDisplay(BT->Lchild);
if (BT->Rchild != NULL)
{
cout << ',';
}
LinkBTreeDisplay(BT->Rchild);
cout << ')';
}
}
}
int LinkBTreeWidth(LinkBTree *BT)//求二叉链的宽度
{
return 0;
}
int LinkBTreeNodes(LinkBTree * BT)//求节点个数
{
if (BT == NULL)
{
return 0;
}
else if (BT->Lchild == NULL && BT->Rchild == NULL) //为叶子节点的情况
{
return 1;
}
else
{
return (LinkBTreeNodes(BT->Lchild) + LinkBTreeNodes(BT->Rchild) + 1);
}
}
int LinkBTreeLeafNodes(LinkBTree *BT)//求二叉链的叶子节点个数
{
if (BT == NULL)
{
return 0;
}
else if (BT->Lchild == NULL && BT->Rchild == NULL) //为叶子节点的情况
{
return 1;
}
else
{
return (LinkBTreeLeafNodes(BT->Lchild) + LinkBTreeLeafNodes(BT->Rchild));
}
}
void LinkBTreeProOeder(LinkBTree *BT) //前序非递归遍历
{
LinkBTree *St[MaxSize], *p;
int top = -1;
if (BT != NULL)
{
top++;
St[top] = BT; //将第一层指向根节点
while (top > -1)
{
p = St[top]; //第一层
top--; //退栈并访问该节点
cout << p->Elem << " ";
if (p->Rchild != NULL)
{
top++;
St[top] = p->Rchild;
}
if (p->Lchild != NULL)
{
top++;
St[top] = p->Lchild;
}
}
cout << endl;
}
}
void LinkBTreeProOederRecursion(LinkBTree *BT)//前序递归遍历
{
if (BT != NULL)
{
cout << BT->Elem<<" ";
LinkBTreeProOeder(BT->Lchild);
LinkBTreeProOeder(BT->Rchild);
}
}
void LinkBTreeInOeder(LinkBTree *BT)//中序非递归遍历
{
LinkBTree *St[MaxSize], *p;
int top = -1;
if (BT != NULL)
{
p = BT;
while (top > -1 || p != NULL)
{
while (p != NULL)
{
top++;
St[top] = p;
p = p->Lchild;
}
if (top> -1)
{
p = St[top];
top--;
cout << p->Elem <<" ";
p = p->Rchild;
}
}
cout << endl;
}
}
void LinkBTreeInOederRecursion(LinkBTree *BT)//中序递归遍历
{
if (BT != NULL)
{
LinkBTreeProOeder(BT->Lchild);
cout << BT->Elem << " ";
LinkBTreeProOeder(BT->Rchild);
}
}
void LinkBTreePostOeder(LinkBTree *BT)//后序非递归遍历
{
LinkBTree *St[MaxSize], *p;
int top = -1,flag;
if (BT != NULL)
{
do
{
while (BT != NULL)
{
top++;
St[top] = BT;
BT = BT->Lchild;
}
p = NULL;
flag = 1;
while (top != -1 && flag)
{
BT = St[top];
if (BT->Rchild == p)
{
cout << BT->Elem << " ";
top--;
p = BT;
}
else
{
BT = BT->Lchild;
flag = 0;
}
}
} while (top != -1);
cout << endl;
}
}
void LinkBTreePostOederRecursion(LinkBTree *BT)//后序递归遍历
{
if (BT != NULL)
{
LinkBTreeProOeder(BT->Lchild);
LinkBTreeProOeder(BT->Rchild);
cout << BT->Elem << " ";
}
}5.2、哈夫曼树
在许多应用上,常常将树中的节点附上一个有着某种意义的数值,称此数值为该节点的权,从树根节点到该节点的路径长度与该节点权值之积称为带权路径长度。树中所有叶子节点的带权路径长度之和称为该树的带权路径长度,如下:
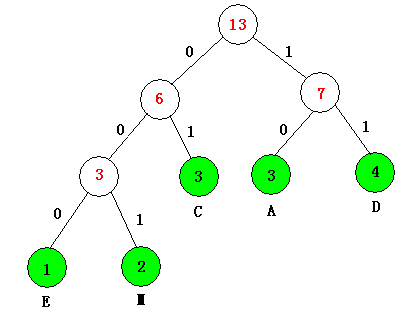
?其中共有n个叶子节点的数目,Wi表示叶子节点i的权值,Li表示根节点到叶子节点的路径长度。
在n个带有权值结点构成的二叉树中,带权路径长度WPL最小的二叉树称为哈夫曼树。又称最优二叉树。
哈夫曼树算法:
(1)根据给定的n个权值,使对应节点构成n颗二叉树的森林T,其中每颗二叉树中都只有一个带权值的Wi的根节点,其左右节点均为空
(2)在森林中选取两颗根节点权值最小的子树分别作为左、右子树构造一颗新二叉树,且置新的二叉树的根节点的权值为其左、右子树上根节点的权值之和。
(3)在森林中,用新得到的二叉树代替选取的两棵树
(4)重复(2)和(3),直到T只含一棵树为止
定理:对于具有n个叶子节点的哈夫曼树,共有2n-1个节点
代码如下:
#pragma once
typedef double Wi; //假设权值为双精度
struct HTNode //每一个节点的结构内容,
{
Wi weight; //节点的权值
HTNode *left; //左子树
HTNode *right; //右子树
};
void PrintHuffman(HTNode * HuffmanTree); //输出哈夫曼树
HTNode * CreateHuffman(Wi a[], int n); //创建哈夫曼树#include"Huffman.h"
#include<iostream>
/*
哈夫曼算法:
(1)根据给定的n个权值创建n个二叉树的森林,其中n个二叉树的左右子树均为空
(2)在森林中选择权值最小的两个为左右子树构造一颗新树,根节点
为权值最小的之和
(3)在森林中,用新的树代替选取的两棵树
(4)重复(2)和(3)
定理:n个叶子节点的哈夫曼树共有2n-1个节点
*/
/*
a[] I 存放的是叶子节点的权值
n I 叶子节点个数
return O 返回一棵哈夫曼树
*/
HTNode* CreateHuffman(Wi a[], int n) //创建哈夫曼树
{
int i, j;
HTNode **Tree, *HuffmanTree; //根据n个权值声明n个二叉树的森林,二级指针表示森林(二叉树的集合)
Tree = (HTNode**)malloc(n * sizeof(HTNode)); //代表n个叶节点,为n棵树分配内存空间
HuffmanTree = (HTNode*)malloc(sizeof(HTNode));
//实现第一步:创建n棵二叉树,左右子树为空
for (i = 0; i < n; i++)
{
Tree[i] = (HTNode*)malloc(sizeof(HTNode));
Tree[i]->weight = a[i];
Tree[i]->left = Tree[i]->right = nullptr;
}
//第四步:重复第二和第三步
for (i = 1; i < n; i++) //z这里表示第i次排序
{
//第二步:假设权值最小的根节点二叉树下标为第一个和第二个
//打擂台选择最小的两个根节点树
int k1 = 0, k2 = 1;
for (j = k2; j < n; j++)
{
if (Tree[j] != NULL)
{
if (Tree[j]->weight < Tree[k1]->weight) //表示j比k1和k2的权值还小,因此两个值都需要更新
{
k2 = k1;
k1 = j;
}
else if(Tree[j]->weight < Tree[k2]->weight) //k1 < j < k2,需要更新k2即可
{
k2 = j;
}
}
}
//第三步:一次选择结束后,将更新一颗树
HuffmanTree = (HTNode*)malloc(sizeof(HTNode)); //每次一轮结束,创建一个根节点
HuffmanTree->weight = Tree[k1]->weight + Tree[k2]->weight; //更新后的根节点权值为左右子树权值之和
HuffmanTree->left = Tree[k1]; //最小值点为左子树
HuffmanTree->right = Tree[k2]; //第二小点为右子树
Tree[k1] = HuffmanTree;
Tree[k2] = nullptr;
}
free(Tree);
return HuffmanTree;
}
//先序遍历哈夫曼树
void PrintHuffman(HTNode * HuffmanTree) //输出哈夫曼树
{
if (HuffmanTree == nullptr)
{
return;
}
std::cout << HuffmanTree->weight;
if (HuffmanTree->left != nullptr || HuffmanTree->right != nullptr)
{
std::cout << "(";
PrintHuffman(HuffmanTree->left);
if (HuffmanTree->right != nullptr)
{
std::cout << ",";
}
PrintHuffman(HuffmanTree->right);
std::cout << ")";
}
}6、查找算法
6.1、线性表查找(顺序查找、折半查找)
顺序查找
#include<iostream>
using namespace std;
#define Max 100
typedef int KeyType;
typedef char InfoType[10];
typedef struct
{
KeyType key; //表示位置
InfoType data; //data是具有10个元素的char数组
}NodeType;
typedef NodeType SeqList[Max]; //SeqList是具有Max个元素的结构体数组
int SeqSearch(SeqList R, int n, KeyType k)
{
int i = 0;
while (i < n && R[i].key != k)
{
cout << R[i].key;//输出查找过的元素
i++;
}
if (i >= n)
{
return -1;
}
else
{
cout << R[i].key << endl;
return i;
}
}
int main()
{
SeqList R;
int n = 10;
KeyType k = 5;
int a[] = { 3,6,8,4,5,6,7,2,3,10 },i;
for (int i = 0; i < n; i++)
{
R[i].key = a[i];
}
cout << endl;
if ((i = SeqSearch(R, n, k)) != -1)
cout << "元素" << k << "的位置是" << i << endl;
system("pause");
return 0;
}折半查找
#include<iostream>
using namespace std;
#define Max 100
typedef int KeyType;
typedef char InfoType[10];
typedef struct
{
KeyType key;
InfoType data;
}NodeType;
typedef NodeType SeqList[Max];
int BinSeqList(SeqList R, int n, KeyType k)
{
int low = 0, high = n - 1, mid, cout = 0;
while (low <= high)
{
mid = (low + high) / 2;
//cout << "第" << ++cout << "次查找:" << "在" << "[" << low << "," << high << "]" << "中查找到元素:" << R[mid].key << endl;
if (R[mid].key == k)
{
return mid;
}
if (R[mid].key > k)
high = mid - 1;
else
low = mid + 1;
}
}
int main()
{
SeqList R;
KeyType k = 9;
int a[] = { 1,2,3,4,5,6,7,8,9,10 },i,n = 10;
for (i = 0; i < n; i++)
{
R[i].key = a[i];
}
cout << endl;
if ((i = BinSeqList(R, n, k)) != -1)
{
cout << "元素" << k << "的位置是:" << i << endl;
}
system("pause");
return 0;
}6.2、树表查找(二叉排序树、平衡二叉树、B-树、B+树)
二叉排序树(B树)
#pragma once
#ifndef BSTREE_H
#define BSTREE_H
#define Max 100
typedef int KeyType;
typedef char InfoType[10];
typedef struct node
{
KeyType key; //关键字项
InfoType data; //其他数据项
struct node *Lchild, *Rchild;
}BSTNode;
BSTNode *BSTreeCreat(KeyType A[], int n); //由数组A(含有n个关键字)中的关键字创建一个二叉排序树
int BSTreeInsert(BSTNode *& BST, KeyType k); //在以*BST为根节点的二叉排序树中插入一个关键字为k的结点
int BSTreeDelete(BSTNode *& BST, KeyType k); //在bst中删除关键字为k的结点
void BSTreeDisplay(BSTNode * BST); //以括号法输出二叉排序树
int BSTreeJudge(BSTNode * BST); //判断BST是否为二叉排序树
#endif#include<iostream>
#include"BSTree.h"
using namespace std;
BSTNode *BSTreeCreat(KeyType A[], int n) //由数组A(含有n个关键字)中的关键字创建一个二叉排序树
{
BSTNode *BST = NULL;
int i = 0;
while (i < n)
{
if(BSTreeInsert(BST,A[i]) == 1)
{
cout << "第" << i + 1 << "步,插入" << A[i] << endl;
BSTreeDisplay(BST);
cout << endl;
i++;
}
}
return BST;
}
int BSTreeInsert(BSTNode *& BST, KeyType k) //在以*BST为根节点的二叉排序树中插入一个关键字为k的结点
{
if (BST == NULL)
{
BST = (BSTNode *)malloc(sizeof(BSTNode));
BST->key = k;
BST->Lchild = BST->Rchild = NULL;
return 1;
}
else if(k == BST->key)
{
return 0;
}
else if(k > BST->key)
{
return BSTreeInsert(BST->Rchild, k);
}
else
{
return BSTreeInsert(BST->Lchild, k);
}
}
int BSTreeDelete(BSTNode *& BST, KeyType k) //在bst中删除关键字为k的结点
{
if (BST == NULL)
{
return 0;
}
else
{
if (k < BST->key)
{
return BSTreeDelete(BST->Lchild, k);
}
else if (k>BST->key)
{
return BSTreeDelete(BST->Rchild, k);
}
else
{
Delete(BST)
}
}
}
void BSTreeDisplay(BSTNode * BST) //以括号法输出二叉排序树
{
if (BST != NULL)
{
cout << BST->key;
if (BST->Lchild != NULL || BST->Rchild != NULL)
{
cout << '(';
BSTreeDisplay(BST->Lchild);
if (BST->Rchild != NULL)
{
cout << ',';
}
BSTreeDisplay(BST->Rchild);
cout << ')';
}
}
}
KeyType predt = -32767;
int BSTreeJudge(BSTNode * BST) //判断BST是否为二叉排序树
{
int b1, b2;
if (BST == NULL)
{
return 1;
}
else
{
b1 = BSTreeJudge(BST->Lchild);
if (b1 == 0 || predt >= BST->key)
{
return 0;
}
predt = BST->key;
b2 = BSTreeJudge(BST->Rchild);
return b2;
}
}
void Delete(BSTNode*& p) //删除二叉排序树*p节点
{
BSTNode* q;
if (p->Rchild == nullptr) //当删除的节点没有右子树,只有左子树时,根据二叉树的特点,
{ //直接将左子树根节点放在被删节点的位置。
q = p;
p = p->Lchild;
free(p);
}
else if (p->Lchild == nullptr) //当删除的结点没有左子树,只有右子树时,根据二叉树的特点,
{ //直接将右子树结点放在被删结点位置。
q = p;
p = p->Rchild;
free(p);
}
else
{
Delete1(p, p->Lchild); //当被删除结点有左、右子树时
}
}
void Delete1(BSTNode* p, BSTNode* &r) //当删除的二叉排序树*P节点有左右子树的删除过程
{
BSTNode *q;
if (p->Lchild != nullptr)
{
Delete1(p, p->Rchild); //递归寻找最右下节点
} //找到了最右下节点*r
else //将*r的关键字赋值个*p
{
p->key = r->key;
q = r;
r = r->Lchild;
free(q);
}
}平衡二叉树:若一棵二叉树中的每个节点的左右子树高度至多相差1,则称此二叉树为平衡二叉树。其中平衡因子的定义为:平衡二叉树中每个节点有一个平衡因子,每个节点的平衡因子是该节点左子树高度减去右子树的高度,若每个平衡因子的取值为0,-1,1则该树为平衡二叉树。
B-树
用作外部查找的数据结构,其中的数据存放在外存中,是一种多路搜索树。
1、所有的叶子节点放在同一层,并且不带信息
2、树中每个节点至多有m棵子树
3、若根节点不是终端节点,则根节点至少有两棵子树
4、除根节点外的非叶子节点至少有m/2棵子树
5、每个节点至少存放m/2-1个至多m-1个关键字
6、非叶子节点的关键字数=指向儿子指针的个数-1
7、非叶子节点的关键字依次递增
8、非叶子节点指针:P[1],P[2],...P[m];其中P[i]指向关键字小于K[1]的子树,P[i]指向关键字属于(K[i-1],K[i])的子树
6.3、哈希表查找
从根本上说,一个哈希表包含一个数组,通过特殊的索引值(键)来访问数组中的元素。
哈希表的主要思想是通过一个哈希函数,在所有可能的键与槽位之间建立一张映射表。哈希函数每次接收一个键将返回与键对应的哈希编码或者哈希值。键的数据类型可能多种多样,但哈希值只能是整型。
计算哈希值和在数组中进行索引都只消耗固定的时间,因此哈希表的最大亮点在于它是一种运行时间在常量级的检索方法。当哈希函数能够保证不同的键生成的哈希值互不相同时,就说哈希值能直接寻址想要的结果。
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快地定位。
实际工作中需视不同的情况采用不同的哈希函数,通常考虑的因素有:
- 计算哈希函数所需时间
- 关键字的长度
- 哈希表的大小
- 关键字的分布情况
- 记录的查找频率
1. 直接寻址法:取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a·key + b,其中a和b为常数(这种散列函数叫做自身函数)。若其中H(key)中已经有值了,就往下一个找,直到H(key)中没有值了,就放进去。这种哈希函数计算简单,并且不可能有冲突产生,当关键字连续时,可用直接寻址法;否则关键字的不连续将造成内存单元的大量浪费。
2. 数字分析法:分析一组数据,比如一组员工的出生年月日,这时我们发现出生年月日的前几位数字大体相同,这样的话,出现冲突的几率就会很大,但是我们发现年月日的后几位表示月份和具体日期的数字差别很大,如果用后面的数字来构成散列地址,则冲突的几率会明显降低。因此数字分析法就是找出数字的规律,尽可能利用这些数据来构造冲突几率较低的散列地址。
3. 平方取中法:当无法确定关键字中哪几位分布较均匀时,可以先求出关键字的平方值,然后按需要取平方值的中间几位作为哈希地址。这是因为:平方后中间几位和关键字中每一位都相关,故不同关键字会以较高的概率产生不同的哈希地址。
4、除留取余法:用关键字k除以某个不大于哈希表长度m的数p,将所得的余数作为哈希地址的方法。h(k) = k mod p,其中p取不大于m的素数最佳
#pragma once
#define MaxSize 20 //此处表示哈希表长度m
#define NULLKEY -1 //表示该节点为空节点,未存放数据
#define DELEKEY -2 //表示该节点数据被删除,
typedef int Key; //关键字类型
typedef struct
{
Key key; //关键字值
int count; //探查次数
}HashTable[MaxSize];
void HTInsert(HashTable HT,int &n,Key k,int p); //将关键字插入哈希表中
void HTCreate(HashTable HT, Key x[], int n, int m, int p); //创建哈希表
int HTSearch(HashTable HT, int p, Key k); //在哈希表中查找关键字
int HTDelete(HashTable HT, int p, Key k, int &n); //删除哈希表中关键字k
void HTDisplay(HashTable HT,int n,int m);#include"HT.h"
#include<iostream>
/*解决冲突用开地址的线性探查法*/
void HTInsert(HashTable HT, int &n, Key k, int p) //将关键字k插入哈希表中
{
int i,addr; //i:记录探查数;adddr:记录哈希表下标
addr = k % p;
if (HT[addr].key == NULLKEY || HT[addr].key == DELEKEY) //表示该出为空,可以存储值
{
HT[addr].key = k;
HT[addr].count = 1;
}
else //表示存在哈希冲突
{
i = 1;
do
{
addr = (addr + 1) % p; //哈希冲突解决办法:开地址法中的线性探查法,从当前冲突地址开始依次往后排查
i++;
} while (HT[addr].key != NULLKEY || HT[addr].key != DELEKEY);
}
n++;//表示插入一个元素后哈希表共存储的元素数量
}
/*
HT I/O 哈希表
x[] I 关键字数组
n I 关键字个数
m I 哈希表长度
p I 为小于m的数p,取不大于m的素数最好
*/
void HTCreate(HashTable HT, Key x[], int n, int m, int p)//创建哈希表
{
for (int i = 0; i < m; i++) //创建一个空的哈希表
{
HT[i].key = NULLKEY;
HT[i].count = 0;
}
int n1 = 0;
for (int i = 0; i < n; i++)
{
HTInsert(HT, n1, x[i], p);
}
}
int HTSearch(HashTable HT, int p, Key k) //在哈希表中查找关键字
{
int addr; //用来保存关键字k在哈希表中的下标
addr = k % p;
while(HT[addr].key != NULLKEY || HT[addr].key != k)
{
addr = (addr + 1) % p; //存在着哈希冲突
}
if (HT[addr].key == k)
return addr;
else
return -1;
}
/*
注:删除并非真正的删除,而是标记
*/
int HTDelete(HashTable HT, int p, Key k, int &n)//删除哈希表中关键字k
{
int addr;
addr = HTSearch(HT, p, k);
if (addr != -1)
{
HT[addr].key = DELEKEY;
n--;
return 1;
}
else
{
return 0;
}
}
void HTDisplay(HashTable HT, int n, int m) //输出哈希表
{
std::cout << " 下标:";
for (int i = 0; i < m; i++)
{
std::cout<< i << " ";
}
std::cout << std::endl;
std::cout << " 关键字:";
for (int i = 0; i < m; i++)
{
std::cout << HT[i].key << " ";
}
std::cout << std::endl;
std::cout << "探查次数:";
for (int i = 0; i < m; i++)
{
std::cout << HT[i].key << " ";
}
std::cout << std::endl;
}7、排序算法
7.1、直接插入排序
//按递增顺序进行直接插入排序
/*
假设待排序的元素存放在数组R[0...n-1]中,排序过程中的某一时刻
R被划分为两个子区间R[0..i-1]和R[i..n-1],其中,前一个子区间
是已排好序的有序区间,后一个则是未排序。直接插入排序的一趟操
作是将当前无序区间的开头元素R[i]插入到有序区间R[0..i-1]中适当
的位置中,使R[0..i]变成新的区间
*/
void InsertSort(RecType R[], int n)
{
int i, j, k;
RecType temp;
for (i = 1; i < n; i++)
{
temp = R[i]; //
j = i - 1;
while (j>=0 && temp.key <R[j].key) //如果无序区间值比有序区间小,有序区间值往后挪
{
R[j + 1] = R[j];
j--;
}
R[j + 1] = temp;
cout << "i:" << i << " ";
for (k = 0; k < n; k++)
{
cout << R[k].key << " ";
}
cout << endl;
}
}7.2、折半插入排序
7.3、希尔排序
//希尔排序
/*
先取定一个小于n的整数d1作为第一个增量,
把表的全部元素分成d1个组,所有相互之间
距离为d1的倍数的元素放在同一个组中,在
各组内进行直接插入排序;然后,取第二个
增量d2,重复上述的分组过程和排序过程,
直至所取的增量dt=1,即所有元素放在同一
组中进行直接插入排序
*/
void ShellInsert(RecType R[], int n)
{
int i, j, d,k;
RecType temp;
d = n / 2;
while (d > 0)
{
for (i = d; i < n; i++)
{
j = i - d;
while (j >= 0 && R[j].key < R[j+d].key)
{
temp = R[j];
R[j] = R[j + d];
R[j + d] = temp;
j = j - d;
}
}
cout << d<<" ";
for (k = 0; k < n; k++)
{
cout << R[k].key << " ";
}
cout << endl;
d = d / 2; //减少增量
}
}7.4、冒泡排序
/****************************************
* function 冒泡排序 *
* param a[] 待排序的数组 *
* param n 数组长度 *
* return 无 *
* good time O(n) *
* avg time O(n^2) *
* bad time O(n^2) *
* space O(1) *
* stable yes *
*****************************************/
void BubbleSort(int a[],int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (a[i] < a[j])
swap(a[i], a[j]);
}
}
}7.5、快速排序
void Quick_Sort(int a[], int left, int right)
{
if (left < right)
{
//1.随机取基准值,然后交换到left那里
// srand(GetTickCount());
// int m = (rand() % (right - left)) + left;
//2.取前中后的中值,然后交换到left那里
// int m = Mid(left, (left + right / 2), right);
// swap(a[m], a[left]);
int midIndex = Partition(a, left, right); //获取新的基准keyindex
Quick_Sort(a, left, midIndex - 1); //左半部分排序
Quick_Sort(a, midIndex + 1, right); //右半部分排序
}
}
void QuickSort(int a[], int n)
{
Quick_Sort(a, 0, n - 1);
}7.6、直接选择排序
/****************************************
* function 选择排序法 *
* param a[] 待排序的数组 *
* param n 数组长度 *
* return 无 *
* good time O(n^2) *
* avg time O(n^2) *
* bad time O(n^2) *
* space O(1) *
* stable no *
*****************************************/
void SelectSort(int a[], int n)
{
int min = 0;
for (int i = 0; i < n; i++)
{
min = i;
for (int j = i + 1; j < n; j++)
{
if (a[j] < a[min])
min = j;
}
if (min != i)
swap(a[min], a[i]);
}
}7.7、堆排序
#include<iostream>
using namespace std;
#define Max 20
typedef int KeyType;
typedef struct
{
KeyType key;
}RecType;
void HeapDisplay(RecType R[], int i, int n) //括号法输出堆
{
if (i < n)
{
cout << R[i].key << " ";
}
if (2 * i <= n || 2 * i + 1 < n)
{
cout << "(";
if (2 * i <= n)
{
HeapDisplay(R, 2 * i, n);
}
cout << ",";
if (2 * i + 1 <= n)
{
HeapDisplay(R, 2 * i + 1, n);
}
cout << ")";
}
}
void HeapSift(RecType R[], int low, int high) //调整堆
{
int i = low, j = 2 * i; //R[j]是R[i]的左孩子
RecType temp = R[i];
while (j <= high)
{
if (j < high && R[j].key < R[j + 1].key)
{
j++;
}
if (temp.key < R[j].key)
{
R[i] = R[j];
i = j;
j = 2 * i;
}
else break;
}
R[i] = temp;
}
/* 堆排序:在排序过程中,将R[1..n]
看成是一颗顺序存储的完全二叉树,
利用完全二叉树中双亲节点和孩子节
点之间的内在关系,在当前无序区中
选择关键字最小或最大的元素
*/
void HeapSort(RecType R[], int n)
{
int i;
RecType temp;
for (i = n / 2; i >= 1; i--)
{
HeapSift(R, i, n);
}
cout << "初始堆为:";
HeapDisplay(R,1,n); //输出初始堆
cout << endl;
for (i = n; i >= 2; i--)
{
temp = R[1];
R[1] = R[i];
R[i] = temp;
HeapSift(R, 1, i - 1); //刷选R[1]结点,得到i-1个结点的堆
cout << "筛选调整得到的堆:";
HeapDisplay(R, 1, i - 1);
}
}
int main()
{
int i, k, n = 10;
KeyType a[] = { 6,8,9,7,0,1,3,2,4,5 };
RecType R[Max];
for (i = 1; i <= n; i++)
{
R[i].key = a[i - 1];
}
cout << endl;
cout << " 初始关键字:";
for (k = 1; k <= n; k++)
{
cout << R[k].key << " ";
}
cout << endl;
for (i = n / 2; i >= 1; i--)
{
HeapSift(R, i, n);
}
HeapSort(R, n);
cout << " 最终结果:";
for (k = 1; k <= n; k++)
{
cout << R[k].key << " ";
}
cout << endl;
system("pause");
return 0;
}7.8、归并排序
7.9、基数排序
8、图
8.1、图的基本概念
在图形结构中,每一个元素可以有零个和多个前驱,也可以有零个和多个后继,也就是说,元素之间的关系是任意的。无论多么复杂的图都是由顶点和边构成。
路径长度:指一条路径上经过的边的数目
连通:图中任意两点都连通,则为连通图,否则为非连通图
强连通:有向图中,图中任意两点都连通,则为强连通图
权:图中每一条边都可以附有一个数值,这种与边相关的数值称为权
顶点的度:在无向图中,某顶点具有的边数为该顶点的度。在有向图中又分为入度和出度,以顶点i为终点的入边的数目,称为入度,以顶点i为起点的出边的数目,称为该顶点的出度,二者之和为该顶点的度。
图的存储结构:邻接矩阵
图的邻接矩阵的表示方式需要一个二维数组来表示。
优点:直观、容易理解,容易判断出任意两个顶点是否有边,容易计算各个顶点的度。
缺点:如果是完全图时,邻接矩阵是最好的方法,但是对于稀疏矩阵,由于它边较少,但是顶点多,这样就会造成空间浪费。
图的存储结构:邻接表
邻接表是图的一种链式存储结构。
8.2、图的遍历
深度优先遍历方法(DFS):从图中某个初始定点出发,首先访问初始点,然后选择一个与顶点相邻且没有被访问的顶点w为初始顶点,在继续从顶点w出发进行深度优先遍历,直到所有人顶点被访问。显然该遍历过程是一个递归过程。(一次访问一个点)
广度优先遍历方法(BFS):首先访问初始点v,接着访问顶点v的所有未被访问过的所有邻接点v1,v2,v3,,,vt,访问每一个顶点的所有未被访问过的邻接点,依次类推。(一次访问所有邻接点)
8.3、生成树和最小生成树
现在假设有一个很实际的问题:我们要在n个城市中建立一个通信网络,则连通这n个城市需要布置n-1一条通信线路,这个时候我们需要考虑如何在成本最低的情况下建立这个通信网??
于是我们就可以引入连通图来解决我们遇到的问题,n个城市就是图上的n个顶点,然后,边表示两个城市的通信线路,每条边上的权重就是我们搭建这条线路所需要的成本,所以现在我们有n个顶点的连通网可以建立不同的生成树,每一颗生成树都可以作为一个通信网,当我们构造这个连通网所花的成本最小时,搭建该连通网的生成树,就称为最小生成树。
普里姆(Prim)算法:
首先就是从图中的一个起点a开始,把a加入U集合,然后,寻找从与a有关联的边中,权重最小的那条边并且该边的终点b在顶点集合:(V-U)中,我们也把b加入到集合U中,并且输出边(a,b)的信息,这样我们的集合U就有:{a,b},然后,我们寻找与a关联和b关联的边中,权重最小的那条边并且该边的终点在集合:(V-U)中,我们把c加入到集合U中,并且输出对应的那条边的信息,这样我们的集合U就有:{a,b,c}这三个元素了,一次类推,直到所有顶点都加入到了集合U。该算法的核心是一次加入一个点,然后添加该点边权值最小的那条,直到所有点都添加进去。
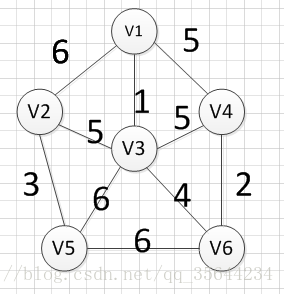
下面我们对下面这幅图求其最小生成树:
?假设我们从顶点v1开始,所以我们可以发现(v1,v3)边的权重最小,所以第一个输出的边就是:v1—v3=1;然后,我们要从v1和v3作为起点的边中寻找权重最小的边,首先了(v1,v3)已经访问过了,所以我们从其他边中寻找,发现(v3,v6)这条边最小,所以输出边就是:v3—-v6=4。
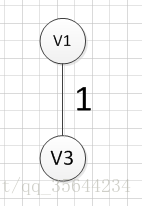 | 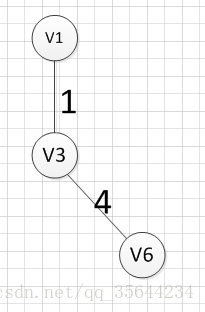 |
?然后,我们要从v1、v3、v6这三个点相关联的边中寻找一条权重最小的边,我们可以发现边(v6,v4)权重最小,所以输出边就是:v6—-v4=2。然后,我们就从v1、v3、v6、v4这四个顶点相关联的边中寻找权重最小的边,发现边(v3,v2)的权重最小,所以输出边:v3—–v2=5 :
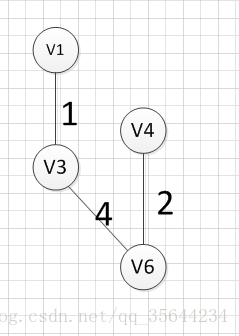 | 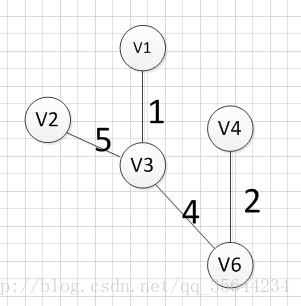 |
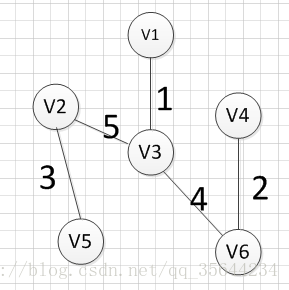
?然后,我们就从v1、v3、v6、v4,v2这2五个顶点相关联的边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以输出边:v2—–v5=3?
?最后,我们发现六个点都已经加入到集合U了,我们的最小生成树建立完成。
代码实现:
#include<iostream>
#include<string>
#define MAXSIZE 100
using namespace std;
struct M_g //定义邻接矩阵
{
string *Head; //顶点表
int **arc; //邻接矩阵可以看成边表
int N_v, N_e; //记录顶点数和边数
};
//创建一个邻接矩阵表示图
void OnCreateM_g(M_g *&x)
{
int i, j, k, w;
cout << "输入顶点个数和边数" << endl;
cin >> x->N_v >> x->N_e; //依次输入顶点数和边数
cout << "顶点数为:" << x->N_v << ";" << "边数为:" << x->N_e << endl;
for (int i = 0; i < x->N_v; i++)
{
cin >> x->Head[i]; //依次输入顶点
}
for (int i = 0; i < x->N_v; i++) //给出每个顶点是否连接
{
for (int j = 0; j < x->N_v; j++)
{
x->arc[i][j] = INT_MAX;
}
}
cout << "输入(Vi,Vj)的上标i,下标j和权w" << endl;
for (k = 0; k < x->N_e; k++) //
{
cin >> i >> j >> w;
x->arc[i][j] = w;
x->arc[j][i] = x->arc[i][j]; //无向图是对称矩阵
}
}
//打印图
void Print(M_g x)
{
int i;
for (i = 0; i < x.N_v; i++)
{
for (int j = 0; j < x.N_v; j++)
{
if (x.arc[i][j] == INT_MAX)
{
cout << "∞" << " ";
}
else
{
cout << x.arc[i][j] << " ";
}
}
cout << endl;
}
}
//记录边的信息,这些边都是达到end的所有边中,权重最小的那个
struct Assis_array
{
int start; //边的起点
int end; //边的终点
int weight;//边的权重
};
//Prim算法实现,图的存储方式为邻接矩阵
void Prim(M_g *x, int begin)
{
//创建一个保存到达某个顶点的各个边中权重最大的那个边的结构体数组
Assis_array *edge = new Assis_array[x->N_v];
int j;
//edge初始化,初始化时用顶点0到该点的边为权值最大边
for (j = 0; j < x->N_v; j++)
{
if (j != begin - 1)
{
edge[j].start = begin - 1;
edge[j].end = j;
edge[j].weight = x->arc[begin - 1][j];
}
}
//将起点的edge的权值设置为-1,表示已经加入到集合U了
edge[begin - 1].weight = -1;
//b访问剩下的顶点,并依次加入到集合U
for (j = 1; j < x->N_v; j++)
{
int min = INT_MAX;
int k;
int index;
//寻找数组权重最小的那边条边
for (k = 0; k < x->N_v; k++)
{
if (edge[k].weight != -1)
{
if (edge[k].weight < min)
{
min = edge[k].weight;
index = k;
}
}
}
//将权重最小的那条边的终点也加入集合U
edge[index].weight = -1;
//输出对应的边的信息
cout << edge[index].start
<< "-----"
<< edge[index].end
<< "="
<< x->arc[edge[index].start][edge[index].end] << endl;
//更新我们的edge数组
for (k = 0; k < x->N_v; k++)
{
if (x->arc[edge[index].end][k] < edge[k].weight)
{
edge[k].weight = x->arc[edge[index].end][k];
edge[k].start = edge[index].end;
edge[k].end = k;
}
}
}
}
int main() {
M_g *p;
p = (M_g*)malloc(sizeof(M_g));
OnCreateM_g(p);
Prim(p,1);
system("pause");
return 0;
}克鲁斯卡(Kruskal)算法:
(1)将图中的所有边都去掉。
(2)将边按照权值从小到大的顺序添加到图中,保证添加的过程中不会形成环
(3)重复以上一步策略直到连接所有顶点,此时就生成了最小生成树。这是一种贪心策略。
模拟克鲁斯卡算法生成最小生成树的详细的过程:
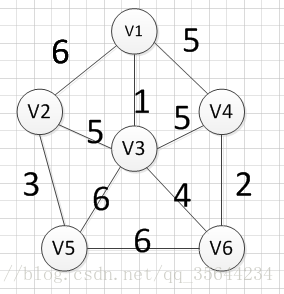
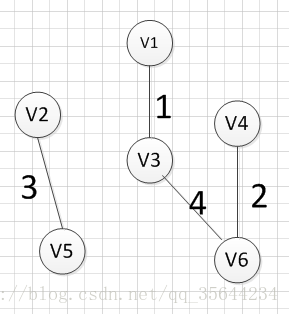
首先完整的图如下图:?
?然后,我们需要从这些边中找出权重最小的那条边,可以发现边(v1,v3)这条边的权重是最小的,所以我们输出边:v1—-v3=1。然后,我们需要在剩余的边中,再次寻找一条权重最小的边,可以发现边(v4,v6)这条边的权重最小,所以输出边:v4—v6=2 。
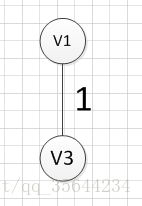 | 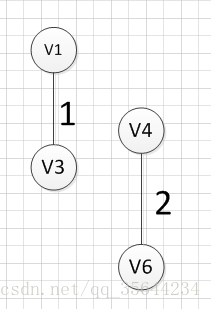 |
?然后,我们再次从剩余边中寻找权重最小的边,发现边(v2,v5)的权重最小,所以可以输出边:v2—-v5=3,?然后,我们使用同样的方式找出了权重最小的边:(v3,v6),所以我们输出边:v3—-v6=4 :
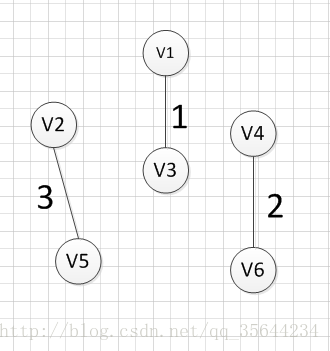 |  |
?好了,现在我们还需要找出最后一条边就可以构造出一颗最小生成树,但是这个时候我们有三个选择:(v1,V4),(v2,v3),(v3,v4),这三条边的权重都是5,首先我们如果选(v1,v4)的话,得到的图如下:?我们发现,这肯定是不符合我们算法要求的,因为它出现了一个环,所以我们再使用第二个(v2,v3)试试,得到图形如下:?
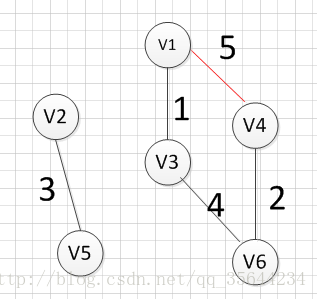 | 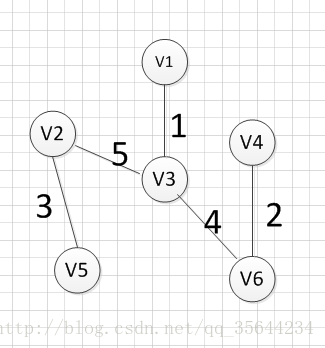 |
?我们发现,这个图中没有环出现,而且把所有的顶点都加入到了这颗树上了,所以(v2,v3)就是我们所需要的边,所以最后一个输出的边就是:v2—-v3=5,最后,我们的最小生成树完成。
8.4、最短路径
最短路径:从一个顶点到另一个顶点可能存在多条路径,每条路径上所经过的边数可能不同,即路径长度不同,把路径长度最短的那条路径叫做最短路径。对于带权的图,应该考虑路径上各边的权值,通常把一条路径上所经过的边的权值之和定为该路径的长度或者带权路径长度。
1、从一个顶点到其余各个顶点的最短路径:狄克斯特拉(Dijkstra)算法
Dijkstra算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。?
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想(BFS)),直到扩展到终点为止。
基本思想
通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。?初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是"起点s到该顶点的路径"。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。... 重复该操作,直到遍历完所有顶点。
操作步骤
(1)?初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为"起点s到该顶点的距离"[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
(2)?从U中选出"距离最短的顶点k",并将顶点k加入到S中;同时,从U中移除顶点k。
(3)?更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4)?重复步骤(2)和(3),直到遍历完所有顶点。
狄克斯特拉算法图解
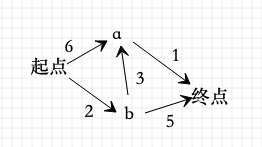
# 创建一个散列表
# 将键映射到值,构建关系网
graph = {}
# 起点
graph["start"] = {}
# 起点的邻居
graph["start"]["a"] = 6
graph["start"]["b"] = 2
# a和b的邻居
graph["a"] = {}
graph["a"]["finish"] = 1
graph["b"] = {}
graph["b"]["finish"] = 5
graph["b"]["a"] = 3
# 终点的邻居
graph["finish"] = {}
# 创建开销的散列表
costs = {}
costs["a"] = 6
costs["b"] = 2
# 假设终点为无穷大
costs["finish"] = float("inf")
# 创建一个存储父节点的散列表 :要计算总权重,父节点起一个过渡阶段,记录之前的权重
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["finish"] = None
# 记录处理过的节点
processed = []
# 找出开销表中的最小节点
def find_lowcosts_node(costs):
# 无穷大
lowcost = float("inf")
lowcost_node = None
# 遍历所有节点
for node in costs:
cost = costs[node]
if cost < lowcost and node not in processed:
# 给lowcost赋每次的最小值
lowcost = cost
# 更新开销最小的节点
lowcost_node = node
return lowcost_node
# 在未处理的开销表中找开销(权重)最小的节点
node = find_lowcosts_node(costs)
# 所有节点都被处理过后结束
while node is not None:
# 找出该节点的权重值
cost = costs[node]
# 找到该节点的邻居
neighbors = graph[node]
# 遍历该节点的所有邻居
for n in neighbors.keys():
# 起点到该节点再到到邻居节点的权重值和
new_costs = cost + neighbors[n]
# 如果起点到该邻居的权重值大于起点到该节点再到该邻居的权重值(经当前节点前往该邻居更近)
if costs[n] > new_costs:
# 更新该邻居开销
costs[n] = new_costs
# 将该邻居的父节点设置为当前节点,(因为经当前节点前往该邻居更近)
parents[n] = node
print(new_costs) # 7 5 6
print(node) # b b a
# 将当前节点标记为处理过
processed.append(node)
# 递归处理剩下的节点
node = find_lowcosts_node(costs)
9、串的模式匹配
9.1、BF算法
算法的基本思想:从主串的第1个字符起和模式串的第一个字符比较,若相等,则继续逐个比较后续字符,否则从主串的第2字符起重新和模式串的字符比较。依次类推,直到模式串t中的每个字符依次和主串s中的一个连续的字符序列相等,则匹配成功。否则匹配不成功。
#include<stdio.h>
//串的定长顺序存储表示
#define MAXSTRLEN 50 // // 用户可在50以内定义最大串长
typedef unsigned char SString[MAXSTRLEN + 1];//0号单元存放串的长度
//返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数值为0。其中,T非空,1<=pos<=StrLength(S)。
int indexBF(SString S, SString T, int pos){
int i = pos, j = 1;
while(i <= len(S) && j <= len(T)){
if(S[i] == T[j]){
i++;
j++;
}else{
i = i - j + 2;//i回到原位置是i - j + 1 ,所以i退到远位置的下一个位置是i - j + 1 + 1
j = 1;
}
}
if(j > len(T)){//如果j > len(T),说明模式串T与S中某子串完全匹配
return i - T[0];//因为i是已经自增过一次了,所以是i-len(T)而不是i-len(T)+1
}else
return 0;
}
void init(SString &S, char str[]){
int i = 0;
while(str[i]!='\0'){
S[i+1] = str[i];
i++;
}
S[i+1] = '\0';
S[0] = i;
}
void printStr(SString Str){
for(int i = 1; i <= Str[0]; i++){
printf("%c", Str[i]);
}
printf("\n");
}
void main(){
SString S ;
init(S, "ababcabcacbab");
printStr(S);
SString T;
init(T, "abcac");
printStr(T);
int index = indexBF(S, T, 1);
printf("index is %d\n", index);
}9.2、KMP算法
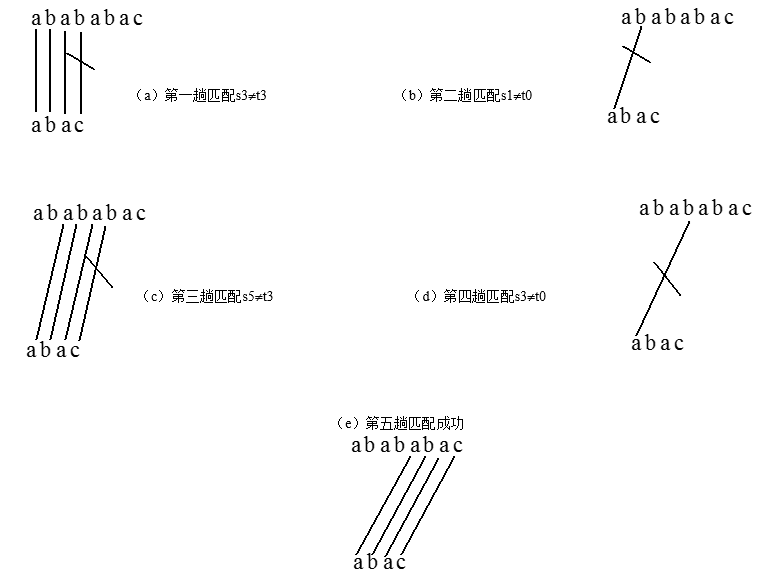
朴素算法会顺序遍历,比较第一次的时候p[0]处失配,然后向后移动继续匹配。数据量大的时候这么做肯定是不可行的。所以这里就会有KMP算法!在一次失配之后,KMP算法认为这里已经失配了,就不能在比较一遍了,而是将字符串P向前移动(已匹配长度-最大公共长度)位,接着继续比较下一个位置。这里已匹配长度好理解,但是最大公共长度是什么呐?这里就出现了next数组,next数组:next[i]表示的是P[0-i]最大公共前后缀公共长度。这里肯定又有人要问了,next数组这么奇葩的定义,为什么就能算出来字符串需要向后平移几位才不会重复比较呐?
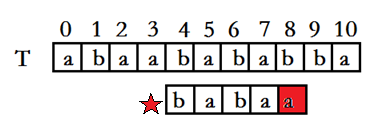
上图中红星标记为例,此时在p[4]处失配,已匹配长度为4,而next[3]=2(也就是babaa中前后缀最大公共长度为0),这时候向后平移已匹配长度-最大公共长度=2位,P[0]到达原来的P[2]的位置,如果只平移一位,P[0]到达p[1]的位置这个位置没有匹配这次操作就是无用功所以浪费掉了时间。已知前缀后缀中的最大公共长度,下次位移的时候直接把前缀位移到后缀上面直接产生匹配,这样直接从后缀的后一位开始比较就可以了。这样将一下无意义的位移过滤掉剩去了不少的时间。
void makeNext(const char P[],int next[])
{
int q,k;
int m=strlen(P);
next[0]=0;
for (q=1,k=0;q<m;++q)
{
while(k>0&&P[q]!=P[k])
k = next[k-1];
/*
这里的while循环很不好理解!
就是用一个循环来求出前后缀最大公共长度;
首先比较P[q]和P[K]是否相等如果相等的话说明已经K的数值就是已匹配到的长的;
如果不相等的话,那么next[k-1]与P[q]的长度,为什么呐?因为当前长度不合适
了,不能增长模板链,就缩小看看next[k-1]
的长度能够不能和P[q]匹配,这么一直递归下去直到找到
*/
if(P[q]==P[k])//如果当前位置也能匹配上,那么长度可以+1
{
k++;
}
next[q]=k;
}
}int kmp(const char T[],const char P[],int next[])
{
int n,m;
int i,q;
n = strlen(T);
m = strlen(P);
makeNext(P,next);
for (i=0,q=0;i<n;++i)
{
while(q>0&&P[q]!= T[i])
q = next[q-1];
/*
这里的循环就是位移之后P的前几个字符能个T模板匹配
*/
if(P[q]==T[i])
{
q++;
}
if(q==m)//如果能匹配的长度刚好是T的长度那么就是找到了一个能匹配成功的位置
{
printf("Pattern occurs with shift:%d\n",(i-m+1));
}
}
}