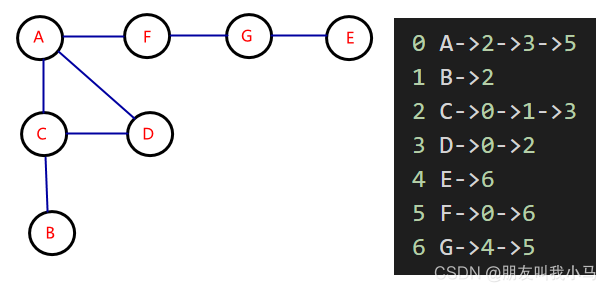
图
图是由一些点vertex和这些点之间的连线边edge组成,通常记作:G = (V, E)。
根据图是否有方向,可以将图划分为:无向图和有向图。
无向图:无向图的边都是不区分方向的。
有向图:不同于无向图,它的所有的边都是有方向的。
邻接点和边
一条边上的两个顶点叫做邻接点。
出边:指的是以该顶点为起点的边。
入边:指的是以该顶点为终点的边。
在无向图中,某个顶点的度是邻接到该顶点的边或数目。
在有向图中,度还有出度和入度之分。
度
入度:指的是以该顶点为终点的变的数目。
出度:指的是以该顶点为起点的边的数目。
顶点的度 = 入度 + 出度。
路径和回路
路径:如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度:路径中“边的数量”。
简单路径:若一条路径上顶点不重复出现,则是简单路径。
回路:若路径的第一个顶点和最后一个顶点相同,则是回路。
简单回路:第一个顶点和最后一个顶点相同,其他各顶点都不重复的回路则是简单回路。
连通图和连通分量
连通图:对于无向图而言,任意两个顶点之间都存在一条无向路径,则称该无向图为连通图。对于有向图而言,任意两个顶点之间都存在一条有向路径,则称该有向图为强连通图。
连通分量:非连通图中各个连通子图称为该图的连通分量。非强连通图的极大强连通子图叫做强连通分量。
生成树
无向连通图的生成树是它的极小连通子图,如果图中含有 n 个顶点,则其生成树由 n -1 条边构成。
若是有向图,则可能得到它的由若干有向树组成的生成森林。
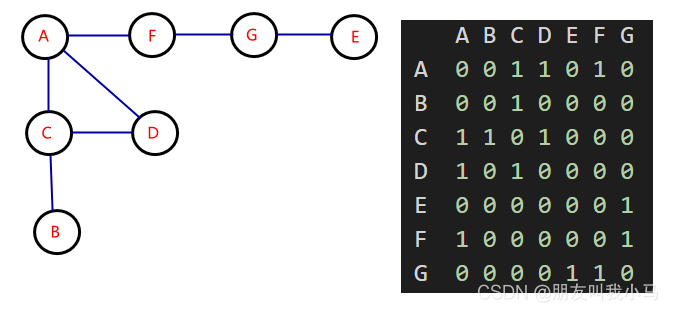
邻接矩阵和邻接表
邻接矩阵用矩阵来表示图。采用矩阵来描述图中顶点之间的关系(及边的权)。
邻接表是图的一种存储方法。它是改进后的邻接矩阵,缺点是不方便判断两个顶点之间是否有边,但是更节省空间。