一、图
1. 图的分类
- 无向图:边没有方向。边与边之间的关系仅仅是连接。
- 有向图:边不仅连接顶点,并具有方向性.
- 带权图:边带着权重。
2. 图的存储结构
- 顺序存储
- 链式存储
线性表:仅有的关系就是线性关系。
树:有清晰的层次关系。
图:集合中每一个元素都可能有关系,图由顶点和边构成,所以要存储图形结构的信息,无非就是存储图的顶点和边。如果使用数组,存储边时会比较复杂。
因此我们采用以下两种存储结构:
-
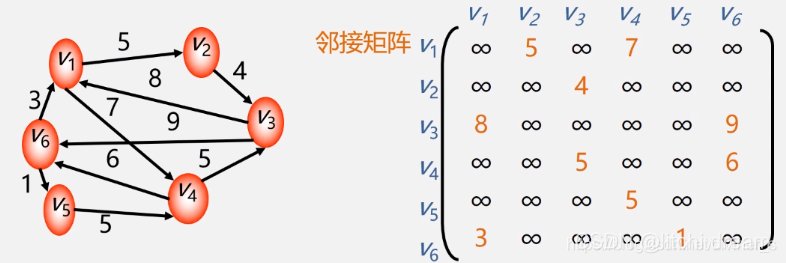
邻接矩阵:n*m数据的集合,矩阵是由行和列组成的一组数表,邻接矩阵让每一个节点和整数相关联。
用1表示有关系,用0表示没关系。
优点:表示非常的明确。
缺点:非常浪费计算机内存空间,存储了太多的0
-
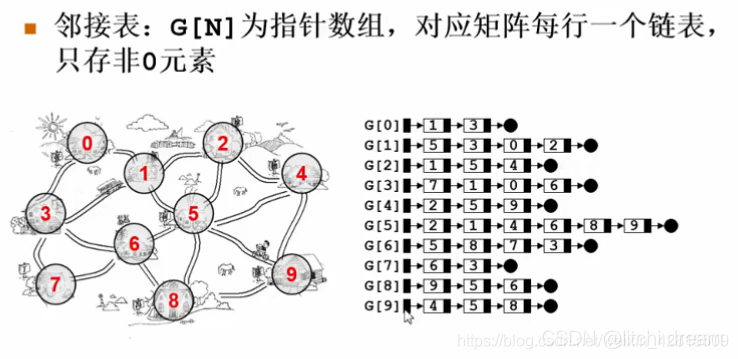
邻接表:由图中每个顶点及与顶点相邻的顶点列表组成。数组、链表、字典
3.实现
// 存储顶点和边,顶点可以使用数组来存
class Graph {
constructor() {
// 存储顶点
this.vertiecs = []
// 存储边
this.edgeList = {}
/**
* A:['B','C','D'] => 键值对的形式
*/
}
// 添加顶点
addVerTex(v) {
this.vertiecs.push(v)
this.edgeList[v] = []
}
// 添加边
addEdge(a, b) {
// 无向图
this.edgeList[a].push(b)
this.edgeList[b].push(a)
}
// 添加toString方法
toString() {
let rst = ''
for (let i = 0; i < this.vertiecs.length; i++) {
// 顶点
let vertex = this.vertiecs[i]
rst += `${vertex}=>`
// 边
let edge = this.edgeList[vertex]
for (let j = 0; j < edge.length; j++) {
rst += edge[j]
}
rst += '\n'
}
return rst
}
}
const graph = new Graph()
// 添加点
graph.addVerTex('A')
graph.addVerTex('B')
graph.addVerTex('C')
graph.addVerTex('D')
graph.addVerTex('E')
graph.addVerTex('F')
// 添加边
graph.addEdge('A', "B")
graph.addEdge('B', "C")
graph.addEdge('B', "F")
graph.addEdge('C', "D")
console.log(graph)
console.log(graph.toString())
4.遍历
遍历:从某个结点触发,一次访问数据结构中全部结点,每个结点访问一次。
- 广度优先遍历 BFC:优先横向遍历图,从图中的某个结点v出发,访问了v后,一次访问v的各个未曾访问过的邻接点,然后分别从这些结点触发,依次访问它们的邻接点,直到所有结点被访问过。
- 深度优先遍历 DFS:先遍历图的纵向。
- 图遍历的思路:
- 每一个顶点有三种状态:
- 未发现(没有发现这个顶点)
- 已经发现(发现其他顶点连接到这里,但是没有发现这个顶点全部的邻接点)
- 已经探索(已经发现这个顶点的所有邻接点)
- 记录顶点是否被访问,使用三种颜色老i标识
- 白色(未发现)
- 灰色(已发现)
- 黑色(已探索)
- 每一个顶点有三种状态:
(1)广度优先遍历
- 广度优先遍历的过程
- 发现未发现的顶点后,存放至队列中,等待查找,并将结点标识为已发现
- 在队列中拿出以发现的结点,开始探索其他顶点,并跳过已探索的顶点
- 遍历完这个顶点以后,将顶点标识为已探索
- 继续在队列中探索下一个顶点
class Queue {
constructor() {
this.items = []
}
// 入队
enqueue(ele) {
this.items.push(ele)
}
// 出队
dequeue() {
return this.items.shift()
}
// 查看队首元素
front() {
return this.items[0]
}
// 查看队尾元素
real() {
return this.items[this.items.length - 1]
}
// 查看队列是否为空
isEmpty() {
return this.items.length === 0
}
// 长度
size() {
return this.items.length
}
// 清空
clear() {
this.items = []
}
}
// 存储顶点和边,顶点可以使用数组来存
class Graph {
constructor() {
// 存储顶点
this.vertiecs = []
// 存储边
this.edgeList = {}
/**
* A:['B','C','D'] => 键值对的形式
*/
}
// 添加顶点
addVerTex(v) {
this.vertiecs.push(v)
this.edgeList[v] = []
}
// 添加边
addEdge(a, b) {
// 无向图
this.edgeList[a].push(b)
this.edgeList[b].push(a)
}
// 添加toString方法
toString() {
let rst = ''
for (let i = 0; i < this.vertiecs.length; i++) {
// 顶点
let vertex = this.vertiecs[i]
rst += `${vertex}=>`
// 边
let edge = this.edgeList[vertex]
for (let j = 0; j < edge.length; j++) {
rst += edge[j]
}
rst += '\n'
}
return rst
}
// 初始化颜色
initColor() {
let colors = {}
for (let i = 0; i < this.vertiecs.length; i++) {
colors[this.vertiecs[i]] = 'white'
}
return colors
}
// 广度优先
bfs(v, callback) {
// 所有结点都设置为白色
let colors = this.initColor()
/**
* colors:{
* 'A':'white',
* 'B':'white',
* }
*/
// 创建队列
let queue = new Queue()
queue.enqueue(v)
while (!queue.isEmpty()) {
// A 出列
const qVertex = queue.dequeue(v)
// 获取A 所有的邻接点
const edge = this.edgeList[qVertex]
// 遍历
for (let i = 0; i < edge.length; i++) {
// 当前节点
const e = edge[i]
if (colors[e] === 'white') {
colors[e] = 'gray'
queue.enqueue(e)
}
}
// A 已经探索,设置为黑色
colors[qVertex] = 'black'
if (callback) {
callback(qVertex)
}
}
}
}
const graph = new Graph()
// 添加点
graph.addVerTex('A')
graph.addVerTex('B')
graph.addVerTex('C')
graph.addVerTex('D')
graph.addVerTex('E')
graph.addVerTex('F')
// 添加边
graph.addEdge('A', "B")
graph.addEdge('A', "C")
graph.addEdge('B', "E")
graph.addEdge('A', "D")
graph.addEdge('B', "F")
graph.bfs('A', (e) => {
console.log(e)
})
(2)深度优先遍历
广度优先遍历使用的是队列,深度优先的原理:递归
深度优先的过程:
- 从某一顶点开始查找,并把结点标识为灰色
- 从这个结点开始探索其他顶点,并跳过已经发现的顶点
- 遍历完这个结点后将这个结点标记为已探索(黑色)
- 递归返回,继续探索下一个路径的最深顶点
// 递归实现深度优先
dfsVisit(v, color, callback) {
color[v] = 'gray'
// 已经被访问到了
if (callback) {
callback(v)
}
// 获取所有的边
let edge = this.edgeList[v]
for (let i = 0; i < edge.length; i++) {
// 当前边
let e = edge[i]
if (color[e] === 'white'){
color[e] = 'gray'
this.dfsVisit(e,color,callback)
}
}
}
// 深度优先遍历
dfs(v, callback) {
const color = this.initColor()
this.dfsVisit(v,color,callback)
}
// 调用深度优先
graph.dfs('A', (e) => {
console.log(e)
})
5.最短路径
最短路径:一个顶点到另一个顶点之间的最短路径。
回溯点:回溯点是离上一个顶点最近的顶点。
回溯路径:由所有回溯点组成。
两种常见的求最短路径的算法:
- 迪杰斯特拉算法:贪心算法的一个应用,解决单源点到其余顶点的最短路径问题。
思想:每次找到离源点(如1号结点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。 - 佛洛依德算法:经典动态规划应用,解决多源最短路径,时间复杂度O(n^3) ,空间复杂度O(n^2)
// 利用广度优先遍历,设置回溯点
// 利用栈来存回溯路径
bfs(v, callback) {
let colors = this.initColor()
let queue = new Queue()
queue.enqueue(v)
// 最短路径
// 所有的回溯点设置为null
let prev = {}
for (let i = 0; i < this.vertiecs.length; i++) {
prev[this.vertiecs[i]] = null
}
while (!queue.isEmpty()) {
const qVertex = queue.dequeue()
const edge = this.edgeList[qVertex]
for (let i = 0; i < edge.length; i++) {
const e = edge[i]
if (colors[e] === 'white') {
colors[e] = 'gray'
// 设置回溯点
prev[e] = qVertex
queue.enqueue(e)
}
}
colors[qVertex] = 'black'
if (callback) {
callback(qVertex)
}
}
return prev
}
const prev = graph.bfs('A')
const shortPath = (from, to) => {
// 当前结点
let vertex = to
let stack = new Stack()
while (vertex !== from) {
// console.log(vertex)
stack.push(vertex)
vertex = prev[vertex] //寻找自己的回溯点
}
stack.push(vertex)
let path = ''
while (!stack.isEmpty()) {
path += `${stack.pop()}=>`
}
return path
}
const path = shortPath('A', 'F')
console.log(path)