题目
给你一个有?n?个节点的 有向无环图(DAG),请你找出所有从节点 0?到节点 n-1?的路径并输出(不要求按特定顺序)
二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点,空就是没有下一个结点了。
注:有向图是有方向的,即规定了 a→b 你就不能从 b→a 。
示例 1:

输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
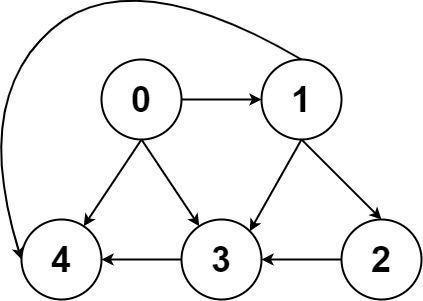
?输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
?示例 3:
输入:graph = [[1],[]] 输出:[[0,1]]
示例 4:?
输入:graph = [[1,2,3],[2],[3],[]] 输出:[[0,1,2,3],[0,2,3],[0,3]]
示例 5:?
输入:graph = [[1,3],[2],[3],[]] 输出:[[0,1,2,3],[0,3]]?
提示:?
n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i(即,不存在自环)
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图(DAG)
题解
方法:深度优先搜索
思路和算法
我们可以使用深度优先搜索的方式求出所有可能的路径。具体地,我们从 0 号点出发,使用栈记录路径上的点。每次我们遍历到点 n-1,就将栈中记录的路径加入到答案中。
特别地,因为本题中的图为有向无环图(DAG),搜索过程中不会反复遍历同一个点,因此我们无需判断当前点是否遍历过。
// C++
class Solution {
public:
vector<vector<int>> ans;
vector<int> stk;
void dfs(vector<vector<int>>& graph, int x, int n) {
if (x == n) {
ans.push_back(stk);
return;
}
for (auto& y : graph[x]) {
stk.push_back(y);
dfs(graph, y, n);
stk.pop_back();
}
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
stk.push_back(0);
dfs(graph, 0, graph.size() - 1);
return ans;
}
};复杂度分析
时间复杂度:O( n × 2^n ),其中 n 为图中点的数量。我们可以找到一种最坏情况,即每一个点都可以去往编号比它大的点。此时路径数为 O(2^n) ,且每条路径长度为 O(n),因此总时间复杂度为 O(n ×?2^n)。
空间复杂度:O(n),其中 n 为点的数量。主要为栈空间的开销。注意返回值不计入空间复杂度。