[数据结构与算法] LeetCode 797：所有可能的路径

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> LeetCode 797：所有可能的路径 -> 正文阅读

[数据结构与算法]LeetCode 797：所有可能的路径

1. 题目描述

给定一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）。
二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点，空就是没有下一个结点了。

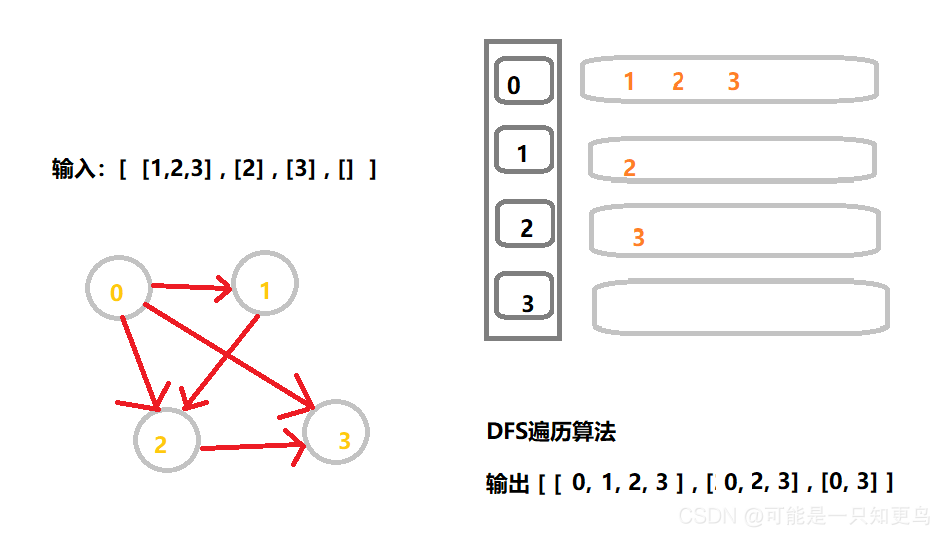
输入：graph = [[1,2,3],[2],[3],[]]

输出：[[0,1,2,3],[0,2,3],[0,3]]

2. 题目分析

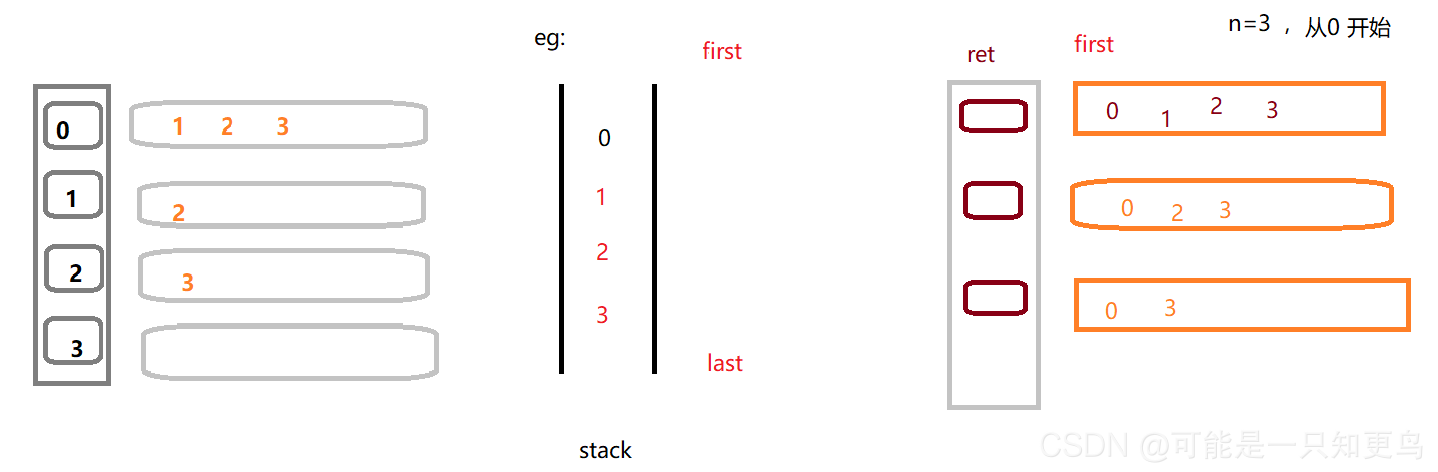
首先我们根据题目描述画出图，并分析输入输出，输入输出都是二维数组，根据题目描述，我们采用深度优先搜索遍历图，求出所有可能的路径。具体，可以从0号位置出发，用栈记录路径上的点，每次当我们找到最终位置后就将其加入到返回列表中；因为操作中不会反复遍历同一个点，所以我们不用标记该点，采用回溯思想即可。
在这里插入图片描述
代码分析

3. 代码实现

class Solution {
    //创建一张二维列表
    List<List<Integer>> ret = new LinkedList<>();
    //创建一个栈，用Deque类来实现
    Deque<Integer> stack = new ArrayDeque<>();
    
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        stack.offerLast(0); //这里必须使用offerLast哦，不然结果是反的，可以一试
        dfs(graph, 0, graph.length-1);
        return ret;
    }

    //dfs深度优先搜索遍历
    public void dfs(int[][] graph, int start, int end){
        if(start==end){
            ret.add(new ArrayList<Integer>(stack));//stack是什么，我就用stack去构造一个ArrayList()对象,将其中的每个元素都放到ArrayList里面
            return;
        }

        for(int x : graph[start]){
            stack.offerLast(x);
            dfs(graph, x, end);
            stack.pollLast();
        }
    }
    
}