[数据结构与算法]【训练题68：Treap上做线段树】UPIT

题意

• 设计一种数据结构，要求能做下述操作：
  （1） $[L,R]$ 区间的数置为 $X$
  （2） $[L,R]$ 区间内的数，第 $i$ 个数字增加 $(i?L+1)X$ ，即加一个等差数列
  （3） 在第 $C$ 个位置前插入一个数字 $X$
  （4） 查询区间 $[L,R]$ 的权值和
• 初始数组 $1\le N\le 10^5$
  操作次数 $1\le Q\le 10^5$

思路

• 首先操作 $1,2,4$ 都是普通的线段树就可以做，但是明显操作 $3$ 只有平衡树才可以做。
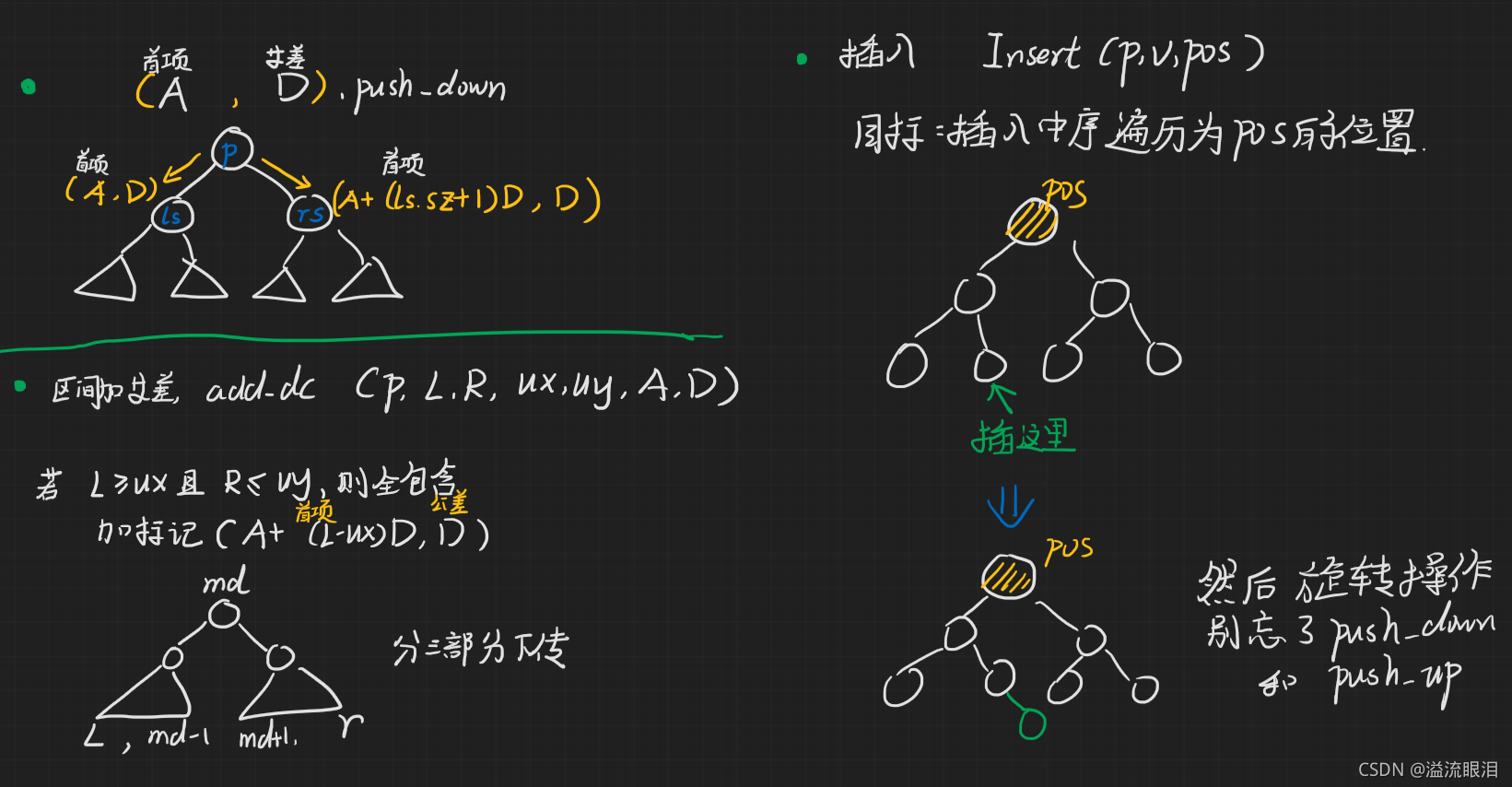
  所以我这里选择相对简单的 $Treap$ 来做。
• 区间置数，只要打一个标记，然后下传即可做。
  查询区间和，类似线段树也好做。
  区间加等差，记一个首项标记和公差标记，然后在 $push\_down$ 的时候下传，注意更新首项标记
  位置插入，只要查看中序遍历的第 $C$ 个位置在哪里，然后插入这个位置的前驱即可。
• 代码由于第一次写，不是特别熟，所以记录一下
  

代码

• 时间复杂度：$O((n+Q)\log n)$

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ls (nd[nd[p].son[0]])
#define rs (nd[nd[p].son[1]])
#define md (L + ls.sz)
void show(){std::cerr << endl;}template<typename T,typename... Args>void show(T x,Args... args){std::cerr << "[ " << x <<  " ] , ";show(args...);}
const int MAX = 2e5+50;
const int INF = 0x3f3f3f3f;
const ll LINF = 0x3f3f3f3f3f3f3f3f;
int Rand(){
    static unsigned long long r=2333;
    return (r*=233333)%=2147483647;
}

ll aa[MAX];
struct node{
    int rval,sz;
    int son[2];
    ll val,A,D,sum;
    ll tag;
}nd[MAX];

int tot,root;
int New(int v){
    ++tot;
    nd[tot].sum = nd[tot].val = v;
    nd[tot].rval = Rand();
    nd[tot].sz = 1;
    nd[tot].son[0] = nd[tot].son[1] = 0;
    nd[tot].A = nd[tot].D = 0;
    nd[tot].tag = -1;
    return tot;
}
inline void push_up(int p){
    nd[p].sum = ls.sum + rs.sum + nd[p].val;
    nd[p].sz = ls.sz + rs.sz + 1;
}
inline void push_down(int p){
    if(~nd[p].tag){
        if(nd[p].son[0]){
            ls.tag = nd[p].tag;
            ls.sum = ls.sz * ls.tag;
            ls.val = nd[p].tag;
        }
        if(nd[p].son[1]){
            rs.tag = nd[p].tag;
            rs.sum = rs.sz * rs.tag;
            rs.val = nd[p].tag;
        }
        ls.D = rs.D = ls.A = rs.A = 0;
    }
    if(nd[p].D){
        if(nd[p].son[0]){
            ll F = nd[p].A;
            ls.D += nd[p].D;
            ls.A += F;
            ls.val += F + nd[ls.son[0]].sz * nd[p].D;
            ls.sum += (F + (F + (ls.sz - 1) * nd[p].D)) * ls.sz / 2;
        }
        if(nd[p].son[1]){
            ll F = nd[p].A + (ls.sz + 1) * nd[p].D;
            rs.D += nd[p].D;
            rs.A += F;
            rs.val += F + nd[rs.son[0]].sz * nd[p].D;
            rs.sum += (F + (F + (rs.sz - 1) * nd[p].D)) * rs.sz / 2;
        }
    }
    nd[p].A = nd[p].D = 0;
    nd[p].tag = -1;
}
inline void Rotate(int &id,int d){ // d=0 left-rotate d=1 right-rotate
    int temp = nd[id].son[d^1];
    nd[id].son[d^1] = nd[temp].son[d];
    nd[temp].son[d] = id;
    id = temp;
    push_up(nd[id].son[d]),push_up(id);
}
// 插入中序遍历的第 pos 个位置
inline void Insert(int &p,int v,int pos){
    if(!p){
        p = New(aa[v]);
        return;
    }
    push_down(p);
    if(pos <= ls.sz + 1){
        Insert(nd[p].son[0],v,pos);
        if(nd[p].rval < ls.rval)Rotate(p,1);
    }else{
        Insert(nd[p].son[1],v,pos - (ls.sz + 1));
        if(nd[p].rval < rs.rval)Rotate(p,0);
    }
    push_up(p);
}
void build(int n){
    root = New(aa[1]);
    for(int i = 2;i <= n;++i){
        Insert(root,i,i);
    }
}

inline void all_set(int p,int L,int R,int ux,int uy,ll k){		// 区间置
    if(!p)return;
    if(L >= ux && R <= uy){
        nd[p].tag = k;
        nd[p].A = nd[p].D = 0;
        nd[p].sum = nd[p].sz * k;
        nd[p].val = k;
        return;
    }
    push_down(p);
    if(ux <= md-1)all_set(nd[p].son[0],L,md-1,ux,uy,k);
    if(uy >= md+1)all_set(nd[p].son[1],md+1,R,ux,uy,k);
    if(md >= ux && md <= uy){
        nd[p].val = k;
    }
    push_up(p);
}
inline void add_dc(int p,int L,int R,int ux,int uy,ll A,ll D){		// 加等差
    if(!p)return;
    if(L >= ux && R <= uy){
        A = A + (L - ux) * D;
        nd[p].A += A;
        nd[p].D += D;
        nd[p].sum += (A + (A + (nd[p].sz - 1) * D)) * nd[p].sz / 2;
        nd[p].val += A + ls.sz * D;
        return;
    }
    push_down(p);
    if(ux <= md-1)add_dc(nd[p].son[0],L,md-1,ux,uy,A,D);
    if(uy >= md+1)add_dc(nd[p].son[1],md+1,R,ux,uy,A,D);
    if(md >= ux && md <= uy){
        nd[p].val += A + (md - ux) * D;
    }
    push_up(p);
}
inline ll query(int p,int L,int R,int ux,int uy){		// 区间求和
    if(!p)return 0;
    ll sum = 0;
    if(L >= ux && R <= uy){
        return nd[p].sum;
    }
    push_down(p);
    if(ux <= md-1)sum += query(nd[p].son[0],L,md-1,ux,uy);
    if(uy >= md+1)sum += query(nd[p].son[1],md+1,R,ux,uy);
    if(md >= ux && md <= uy)sum += nd[p].val;
    return sum;
}
void say(int p){
    show(p,nd[p].val,nd[p].son[0],nd[p].son[1],nd[p].sum);
    if(nd[p].son[0])say(nd[p].son[0]);
    if(nd[p].son[1])say(nd[p].son[1]);
}
int main()
{
    int N,Q;
    N = read();Q = read();
    for(int i = 1;i <= N;++i)aa[i] = read();
    build(N);

    while(Q--){
        int op;
        ll ta,tb,tc;op = read();
        if(op == 1){
            ta = read_ll();tb = read_ll();tc = read_ll();
            all_set(root,1,N,ta,tb,tc);
        }else if(op == 2){
            ta = read_ll();tb = read_ll();tc = read_ll();
            add_dc(root,1,N,ta,tb,tc,tc);
        }else if(op == 3){
            ta = read_ll();tb = read_ll();
            N++;
            aa[N] = tb;
            Insert(root,N,ta);
        }else{
            ta = read_ll();tb = read_ll();
            printf("%lld\n",query(root,1,N,ta,tb));
        }
    }
    return 0;
}