想重新梳理一下知识框架,所以想先从模型入手整理。
线性回归
1.1理论描述
线性回归用来确定自变量和因变量之间相互依赖的定量关系的一种数理统计分析方法。知道了自变量和因变量之间的线性关系,就可以对连续值进行预测。在回归分析中,若只有一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这属于一元线性回归分析,表达式可以写成 y=ax+b ,当给定参数a和b时,输入自变量x就可以输出得到因变量y。但是在实际运用时,因变量的变化往往受两个或两个以上的自变量的影响,且因变量和自变量之间呈线性关系,这种回归分析称为多元线性回归分析。
假设给定一组自变量X,因变量y,
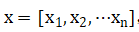
则表达式可写成:
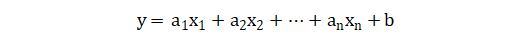
其中,b表示常数项,也称为截距。a为回归系数,那么我们研究的目的就是让我们模型估计的预测值与真实值之间的误差最小,因而我们需要一个最优模型,最优的线性模型依赖于a和b值,继而我们要去找到最优的a和b值。怎么去找到最优的值呢?接下来引入损失函数的概念。
1.2 损失函数 \ 最小二乘估计
损失函数是衡量回归模型误差的函数,也是我们评价标准。损失函数最小,说明我们的模型预测值与真实值之间的差异就越小,模型的性能就越好。那们我们的问题就转化成:利用损失函数来找最优的a和b值。
给定一组样本观测值 (x,y),求解最优回归系数a和常数项b,线性回归就是要找一条直线,并且让这条直线尽可能地拟合这组值 来求。这个时候可以使用最小二乘法来做最优线性估计:残差平方和的值达到最小,说明拟合效果就越好。最小二乘法则是一种最优估计方法,它的目标是最小化误差平方之和来作为目标,从而找到最优模型,这个模型可以拟合(fit)观察数据。
残差平方和的公式可表示为,其中L就是我们的损失函数: 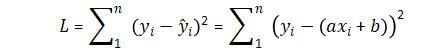
当导数为 0 时,L 取最小值,因此我们分别对a和求偏导并令其为0。
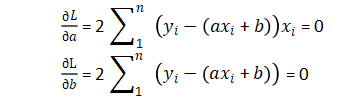
将(x,y)代入上式,就可以求得最优的a和b。确定a和b值之后,即可以确定线性模型,当给定样本观测值x时,就可以预测 y了。
PS:不要混淆了哈,损失函数有很多种,且因为最小二乘估计这个算法比较简单所以会拿出来进行介绍。
因为不太会在博客上面打公式,所以下面附上文件截图,方便大家查看。

