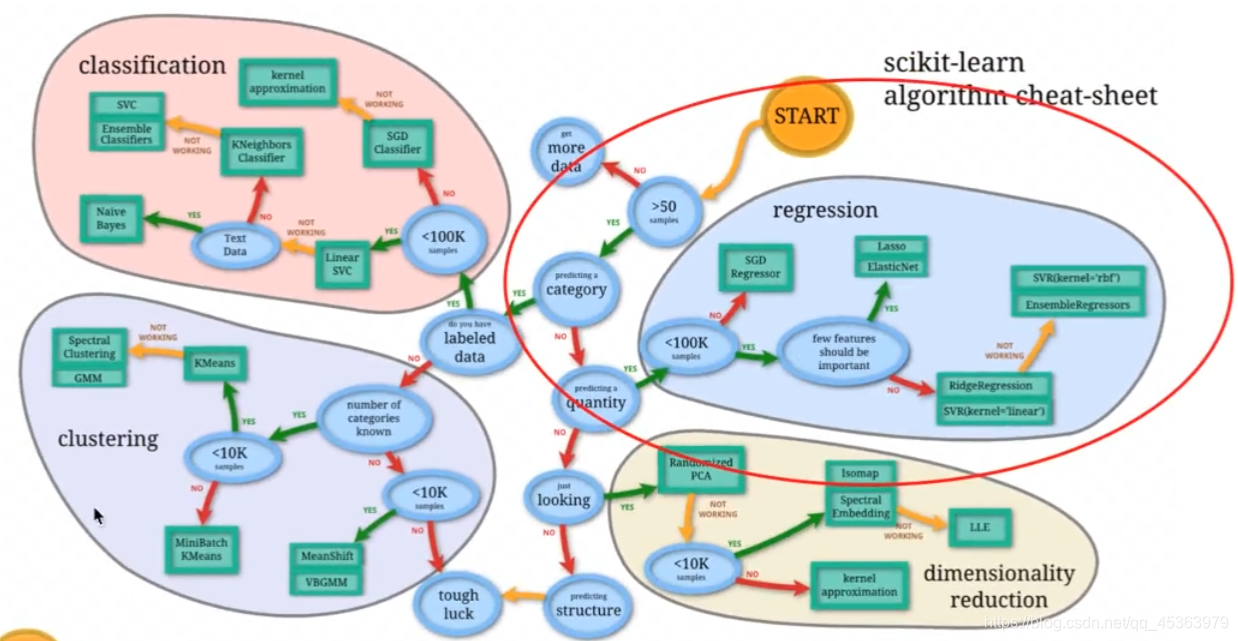
4.1 线性回归

回归问题：目标值-连续型的数据。

4.1.1什么是线性回归

定义与公式：
找到函数关系，表示特征值和目标值，该函数就是线性模型

2.线性回归中线性模型有两种，一种是线性关系，一种是非线性关系。
单特征值与目标值的关系成直线关系，多特征值与目标值呈平面关系。

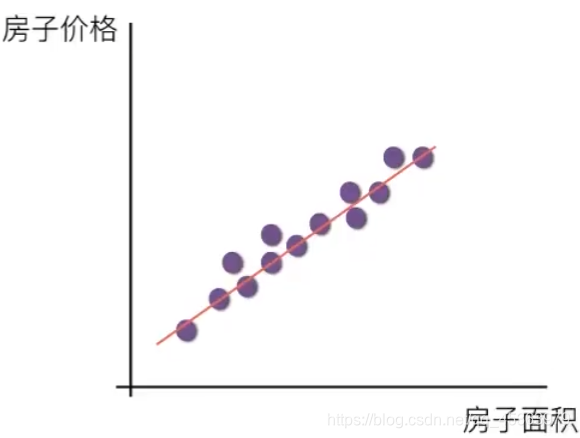
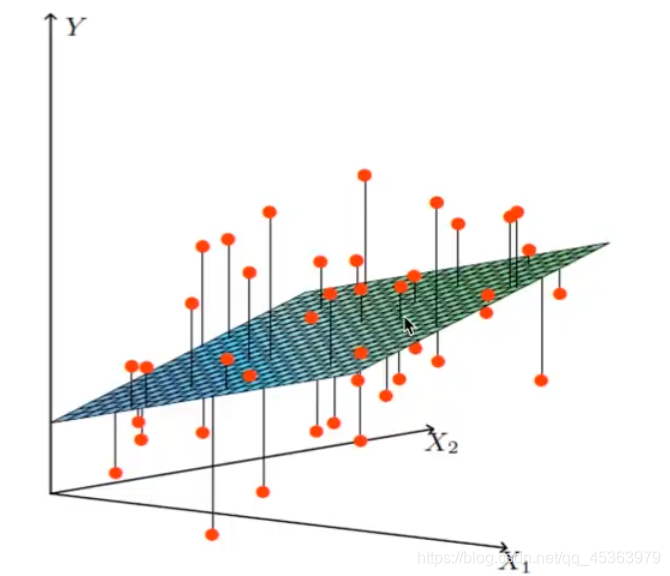
非线性关系：
在这里插入图片描述

线性模型包括线性关系和非线性关系两种
线性模型包括参数一次幂和自变量一次幂线性关系一定是线性模型, 反之不一定
优化方法有两种: 一种是正规方程, 第二种是梯度下降

在这里插入图片描述

4.1.2 线性回归的损失和优化原理

目标求模型参数。

损失函数
优化方法
1）正规方程-直接求解W

2）梯度下降-不断试错，不断改进

3）对比

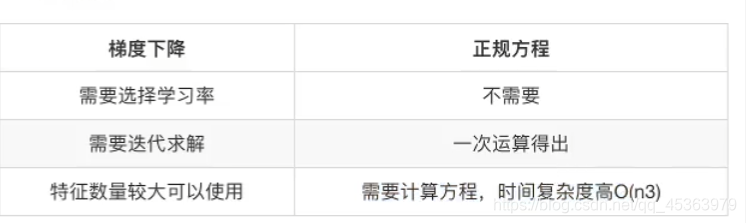
在这里插入图片描述

4.1.3 API

在这里插入图片描述

4.1.4 波士顿房价案例

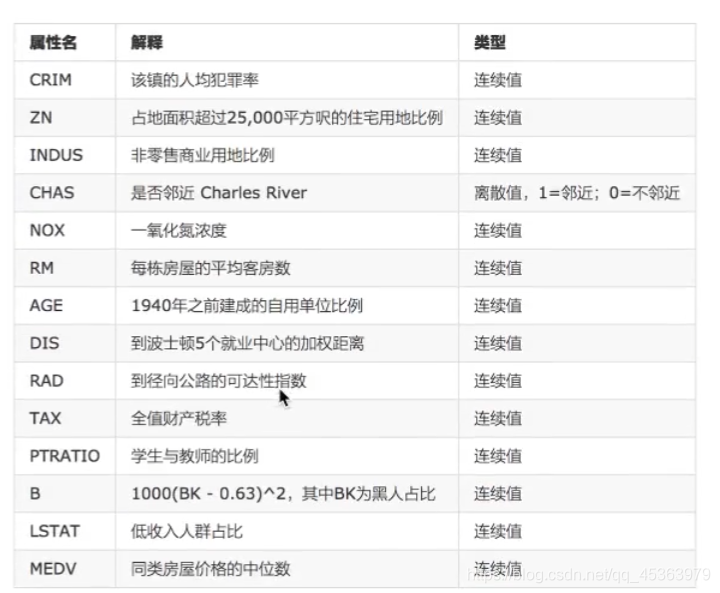
在这里插入图片描述

1）获取数据集
2）划分数据集
3）特征工程：无量纲化-标准化
4）预估器流程：fit() -> 模型 coef_intercept_
5）模型评估
利用均方根误差来进行回归模型评估。

# 线性模型包括线性关系和非线性关系两种
# 线性模型包括参数一次幂和自变量一次幂
# 线性关系一定是线性模型, 反之不一定
# 优化方法有两种: 一种是正规方程, 第二种是梯度下降

# 这部分用来训练预测房价
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error  # 均方误差

def load_data():
    boston_data = load_boston()
    print("特征数量为:(样本数,特征数)", boston_data.data.shape)
    x_train, x_test, y_train, y_test = train_test_split(boston_data.data,
                                                        boston_data.target, random_state=22)
    return x_train, x_test, y_train, y_test


# 正规方程
def linear_Regression():
    """
    正规方程的优化方法
    不能解决拟合问题
    一次性求解
    针对小数据
    :return:
    """
    x_train, x_test, y_train, y_test = load_data()
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    estimator = LinearRegression()
    estimator.fit(x_train, y_train)

    print("正规方程_权重系数为: ", estimator.coef_)
    print("正规方程_偏置为:", estimator.intercept_)

    y_predict = estimator.predict(x_test)
    error = mean_squared_error(y_test, y_predict)
    print("正规方程_房价预测:", y_predict)
    print("正规方程_均分误差:", error)
    return None


# 梯度下降
def linear_SGDRegressor():
    """
    梯度下降的优化方法
    迭代求解
    针对大数据
    :return:
    """
    x_train, x_test, y_train, y_test = load_data()
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 建议看下这个函数的api, 这些值都是默认值
    # estimator = SGDRegressor(loss="squared_loss", fit_intercept=True, eta0=0.01,
    #                          power_t=0.25)

    estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000)
    # estimator = SGDRegressor(penalty='l2', loss="squared_loss")  # 这样设置就相当于岭回归, 但是建议用Ridge方法
    estimator.fit(x_train, y_train)

    print("梯度下降_权重系数为: ", estimator.coef_)
    print("梯度下降_偏置为:", estimator.intercept_)

    y_predict = estimator.predict(x_test)
    error = mean_squared_error(y_test, y_predict)
    print("梯度下降_房价预测:", y_predict)
    print("梯度下降_均分误差:", error)

    return None

if __name__ == '__main__':
    linear_Regression()
    linear_SGDRegressor()