一、逻辑回归基础知识
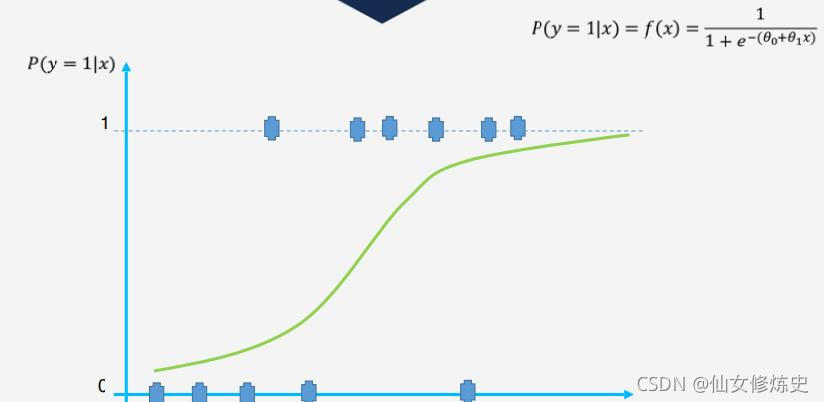
- 解决二元(0/1)分类问题
- P ( y = 1 ∣ x ; θ ) = f ( x ; θ ) = 1 1 + e ? θ T x P(y = 1|x;\theta) = f(x;\theta) = \frac{1}{1+e^{-\theta^Tx}} P(y=1∣x;θ)=f(x;θ)=1+e?θTx1?
- ? θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + . . . -\theta^Tx = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3 +... ?θTx=θ0?+θ1?x1?+θ2?x2?+θ3?x3?+...
- θ = [ θ 0 , θ 1 , θ 2 , θ 3 , . . . ] \theta = [\theta_0, \theta_1,\theta_2,\theta_3,...] θ=[θ0?,θ1?,θ2?,θ3?,...]
- x = [ 1 , x 1 , x 2 , x 3 , . . . ] x = [1, x_1, x_2, x_3,...] x=[1,x1?,x2?,x3?,...]
- 类别为1的概率为: P = 1 1 + e ? θ T x P = \frac{1}{1+e^{-\theta^Tx}} P=1+e?θTx1?
- 类别为0的概率为: 1 ? P = 1 1 + e θ T x 1-P = \frac{1}{1+e^{\theta^Tx}} 1?P=1+eθTx1?
- 类别1与类别0的概率比值: P 1 ? P = e θ T x \frac{P}{1-P} = e^{\theta^Tx} 1?PP?=eθTx
- 类别1与类别0的概率比值的自然对数: l n P 1 ? P = θ T x ln\frac{P}{1-P} = \theta^Tx ln1?PP?=θTx
二、逻辑回归示例
| 年龄( x 1 x_1 x1?) | 年收入( x 2 x_2 x2?)(万元为单位) | 是否买车(1表示是,0表示否) |
|---|---|---|
| 20 | 3 | 0 |
| 23 | 7 | 1 |
| 31 | 10 | 1 |
| 42 | 13 | 1 |
| 50 | 7 | 0 |
| 60 | 5 | 0 |
那么如何你现在30岁,年收入为8,你买车的概率为多大?
from sklearn import linear_model
X = [[20, 3],
[23,7],
[31,10],
[42,13],
[50,7],
[60,5]
]
y = [0,
1,
1,
1,
0,
0
]
lr_reg = linear_model.LogisticRegression()
lr_reg.fit(X, y)
testX = [[30, 8]]
label = lr_reg.predict(testX)
print ("predicted label = ", label)
prob = lr_reg.predict_proba(testX)
print ("probability = ", prob)
结果输出:
predicted label = [1]
probability = [[0.19998365 0.80001635]]
三、逻辑回归系数的意义
通过以上训练,我们可以得到系数
θ
\theta
θ的值:
θ
0
=
?
0.04
,
θ
1
=
?
0.20
,
θ
2
=
0.92
\theta_0 = -0.04, \theta_1 = -0.20, \theta_2 = 0.92
θ0?=?0.04,θ1?=?0.20,θ2?=0.92系数
θ
2
=
0.92
\theta_2=0.92
θ2?=0.92意味着,测试的时候,如果年收入增加1万,一个人买车和不买车的概率比值相较于年收入没有增加的时候,增加
e
0
.
92
=
2.5
倍
e^0.92 = 2.5倍
e0.92=2.5倍
系数
θ
1
=
?
0.20
\theta_1=-0.20
θ1?=?0.20意味着,测试的时候,如果年龄增加1岁,一个人买车和不买车的概率比值相较于年龄没有增加的时候,降低
e
0
?
0.20
=
0.82
倍
e^0-0.20 = 0.82倍
e0?0.20=0.82倍