问题描述
G国国王来中国参观后,被中国的高速铁路深深的震撼,决定为自己的国家也建设一个高速铁路系统。
建设高速铁路投入非常大,为了节约建设成本,G国国王决定不新建铁路,而是将已有的铁路改造成高速铁路。现在,请你为G国国王提供一个方案,将现有的一部分铁路改造成高速铁路,使得任何两个城市间都可以通过高速铁路到达,而且从所有城市乘坐高速铁路到首都的最短路程和原来一样长。请你告诉G国国王在这些条件下最少要改造多长的铁路。
输入格式
输入的第一行包含两个整数n, m,分别表示G国城市的数量和城市间铁路的数量。所有的城市由1到n编号,首都为1号。
接下来m行,每行三个整数a, b, c,表示城市a和城市b之间有一条长度为c的双向铁路。这条铁路不会经过a和b以外的城市。
输出格式
输出一行,表示在满足条件的情况下最少要改造的铁路长度。
样例输入
4 5
1 2 4
1 3 5
2 3 2
2 4 3
3 4 2
样例输出
11
评测用例规模与约定
对于20%的评测用例,1 ≤ n ≤ 10,1 ≤ m ≤ 50;
对于50%的评测用例,1 ≤ n ≤ 100,1 ≤ m ≤ 5000;
对于80%的评测用例,1 ≤ n ≤ 1000,1 ≤ m ≤ 50000;
对于100%的评测用例,1 ≤ n ≤ 10000,1 ≤ m ≤ 100000,1 ≤ a, b ≤ n,1 ≤ c ≤ 1000。输入保证每个城市都可以通过铁路达到首都。
解题思路:
呃。。第一眼看成了求最小生成树的问题,(然后仔细一看其实不是),注意这句话:**而且从所有城市乘坐高速铁路到首都的最短路程和原来一样长。
也就是说每个城市到首都的最短路径必须要修建铁路,找到这个最短路径所需要的最少花费(即要改造的长度最小),即求所有顶点到首都的最短路问题。用spfa算法或者dijstra算法都可以。
不清楚这两个算法的可以看我这两篇文章:
迪杰斯特拉算法求最短路
spfa算法求最短路
不过注意我们需要求出这条路径的最短花费,光借助dis数组保存源点到各点的最短距离是不够的,还需要借助一个cost数组。cost数组里存放的是到这个点的前一条边的最短花费。注意:当某个点加上它的两个前驱边距离长度与源点到这个点的最短距离都相等的时候,我们要找它前驱花费最小的那条边。如图所示:
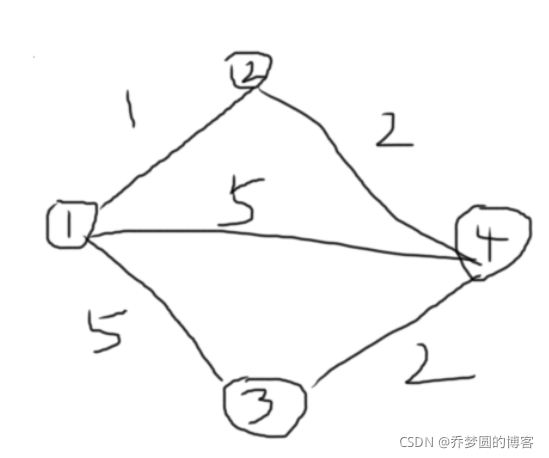
当源点到3的最短距离都是5的时候,我们不能选择1-3这条前驱边,而是选择4-3这条前驱边,因为这条前驱边比1-3的边小,更有利于整体的花费最小。如图:
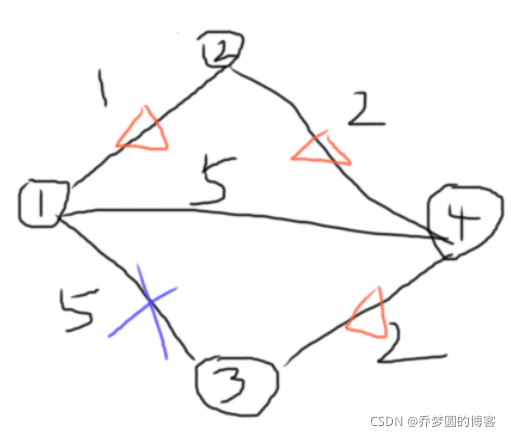
因为最终的答案肯定是由n-1条边构成的生成树,由图看出:选择1-2,2-4,4-3这三条边比1-2,2-4,1-3这三条边整体的花费要少。所以我们最终计算出cost[2]-cost[n]每个顶点的前一条边的最小花费的总和,就是所要求的题目答案。
这里我用的是spfa算法**,下面我们来看代码吧,都有详细注释,方便读者阅读。
#include <bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f
class Edg //定义边类(结构体)
{ public:
int d;//邻接点
int w; //权值(距离或花费)
Edg(int num,int weight)//类的初始化
{ d=num;
w=weight;
}
};
vector<Edg>G[10001];//定义图的邻接表
bool book[10001];//标志数组,表示这个点在不在队列中
int n,m,cost[10001];//n为顶点数,m为边数,cost表示到这个点的前一条边的最小距离
vector<int> dis(10001,inf); //dis存储源点到每一条边的最短距离
void spfa(int source)
{
dis[source]=0;//初始化源点到自身距离为0
queue<int> q;
q.push(source);//源点入队列
while(!q.empty())//当队列非空时
{ int f=q.front(); //取出队首元素
q.pop();//然后把它从队列里踢出去
book[f]=0;//标记为0表示已经不在队列中
int len=G[f].size(),d1,edglen;//len计算出与队首元素这个点相邻的边数
for(int i=0;i<len;i++)//遍历与它相邻的每一条边
{ d1=G[f][i].d;//d1表示与它相邻的点
edglen=G[f][i].w;// edglen表示到这个点的距离(边长)
if(dis[d1]>dis[f]+edglen)//如果源点到这个点的最短距离大于源点到队首元素的距离+队首元素与它的距离
{ dis[d1]=dis[f]+edglen;//进行松弛(更新)
cost[d1]=edglen;//同样到这个点的前一条边的最小距离更新为edglen
if(!book[d1])//如果它不在队列中
{ q.push(d1);//入队列
book[d1]=1;//标记在队列
}
}
else if(dis[d1]==dis[f]+edglen)//如果遇到相等情况
cost[d1]=min(cost[d1],edglen);//找前一条边的最小距离
}
}
}
int main()
{ cin>>n>>m;
int i,start,end,w;
for(i=1;i<=m;i++)
{
cin>>start>>end>>w;
G[start].push_back(Edg(end,w));
G[end].push_back(Edg(start,w));
}
spfa(1);
int ans=0;
for(i=2;i<=n;i++)//把到除源点之外的每一个顶点的前驱边都相加
ans+=cost[i];
cout<<ans;//答案必为n-1条边
}