题目来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems
特别鸣谢:来自夸夸群的 醉笑陪公看落花@知乎,王不懂不懂@知乎
感谢醉笑陪公看落花@知乎 倾囊相授,感谢小伙伴们督促学习,一起进步
参考文章:python中heapq的用法(最小堆) https://blog.csdn.net/weixin_42317507/article/details/92801893
文章目录
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-median-from-data-stream
题目分析
心路历程如下:
-
设计数据结构求中位数,只要左边
a个数都比中位数小,右边b个数都比中位数大就行。abs(a-b)<=1 -
转换为左边
a个数字中最大的数字比中位数小,右边b个数中最小的数字比中位数大就行 -
取集合中的最大和最小,就可以考虑大根堆和小根堆
-
由于python中只封装了小根堆,要存大根堆的时候,我们在小根堆中把数字取一个负号即可实现
-
如果大小根堆的长度一致,则取两个堆顶的数字除以2
-
如果长度不一致,则取堆结点多的那个根堆的堆顶
-
如果插入某个数字,使两个堆的长度差2,则进行调整
方法1 - 草图
假如初始的时候有一些数字在集合中了

方法1 大根堆 小根堆 - 代码 - 通过
addNum : O(log2(n))
findMedian: O(1)
'''
最小堆和最大堆 - 通过
'''
import heapq
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
self.lh = []
self.rh = []
def addNum(self, num: int) -> None:
if len(self.lh) == 0 or num > 0-self.lh[0]:
heapq.heappush(self.rh,num)
else:
heapq.heappush(self.lh, 0-num)
ln = len(self.lh)
rn = len(self.rh)
if ln-rn==2:
heapq.heappush(self.rh,0-heapq.heappop(self.lh))
elif rn - ln==1:
heapq.heappush(self.lh,0-heapq.heappop(self.rh))
else:pass
def findMedian(self) -> float:
ln = len(self.lh)
rn = len(self.rh)
return (0-self.lh[0] + self.rh[0]) / 2 if ln ==rn else float(0-self.lh[0])
方法2 有序列表 - 库函数 - 代码 - 通过
用库函数维护一个有序列表,每次取中间的数字就行
addNum : O(log2(n))
findMedian: O(1)
from sortedcontainers import SortedList
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
self.nums = SortedList()
self.left = 0
self.right = 0
def addNum(self, num: int) -> None:
self.nums.add(num)
def findMedian(self) -> float:
n = len(self.nums)
return (self.nums[n//2]+self.nums[n//2-1])/2 if n%2 ==0 else float(self.nums[n//2])
知识点搜集
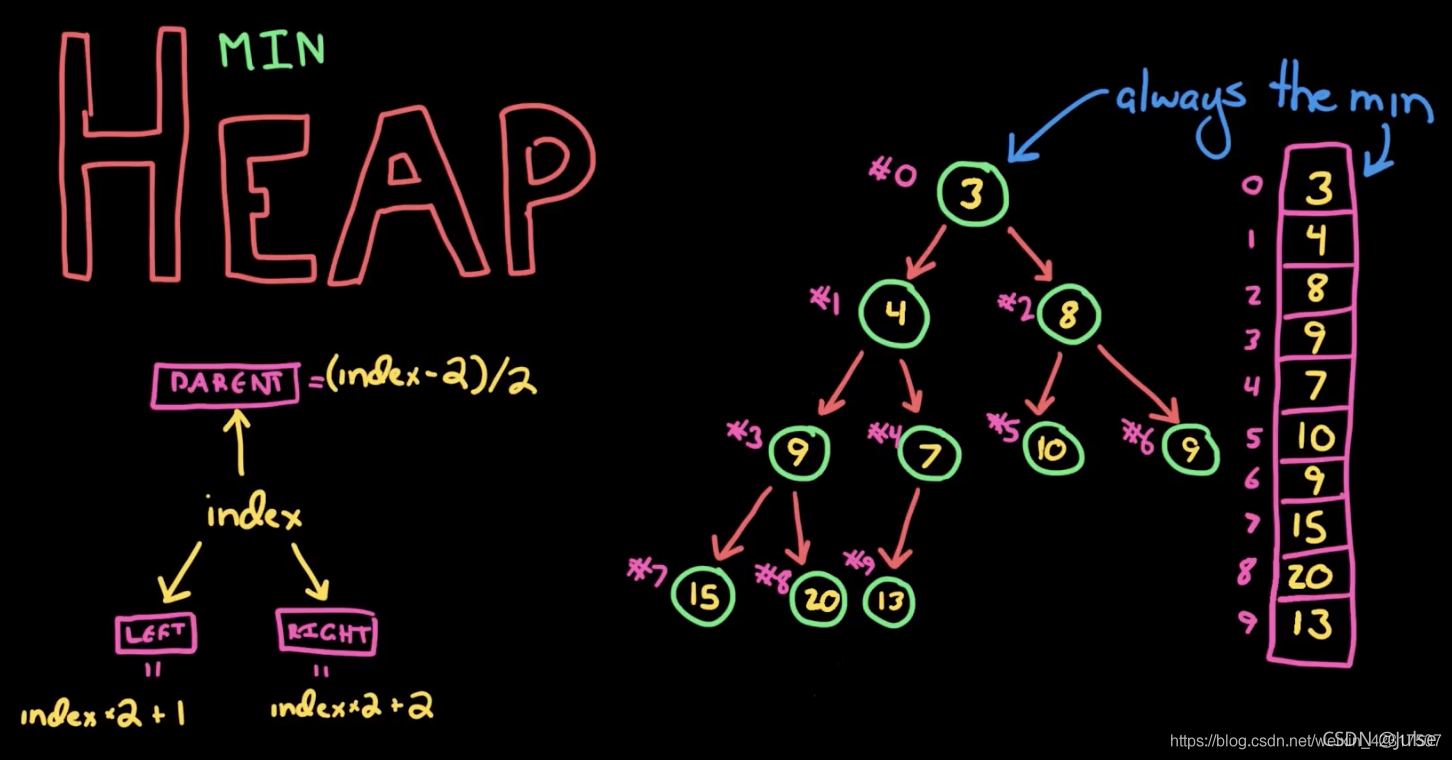
小根堆概念和基本操作- 插入和删除后堆如何变化
孩子节点总是不大于父节点
堆的概念图和基本操作来源 https://blog.csdn.net/weixin_42317507/article/details/92801893
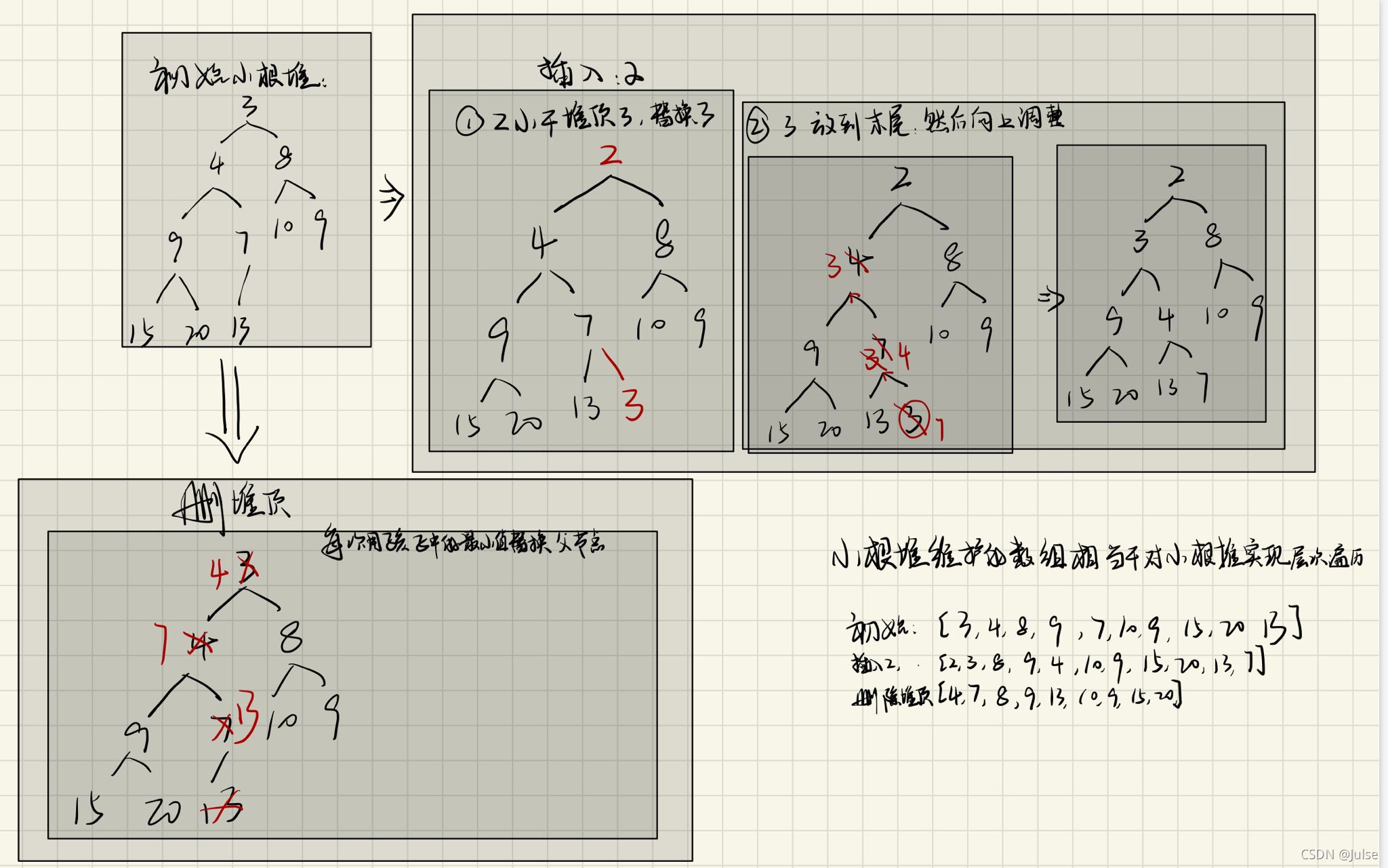
测试这个想法,有空再看看是否是这样调整的
a = [3,4,8,9,7,10,9,15,20,13]
b = a[:]
c = a[:]
heapq.heapify(a)
heapq.heappush(b,2)
heapq.heappop(c)
print(a) # [3, 4, 8, 9, 7, 10, 9, 15, 20, 13]
print(b) # [3, 4, 8, 9, 7, 10, 9, 15, 20, 13]
print(c) # [4, 7, 8, 9, 13, 10, 9, 15, 20]
基本操作记录
import heapq
lst = [1,2,3,5,1,5,8,9,6]
'''
一秒变成堆
'''
heapq.heapify(lst)
[1, 1, 3, 5, 2, 5, 8, 9, 6]
'''
最小的(顶端)再见
'''
heapq.heappop(lst)
[1, 2, 3, 5, 6, 5, 8, 9]
'''
最小的滚蛋,新人进入
'''
heapq.heapreplace(lst,99)
[2, 5, 3, 9, 6, 5, 8, 99]
'''
新人比最小的大,新人进入;若否,则不管
'''
heapq.heappushpop(lst,1)
[2, 5, 3, 9, 6, 5, 8, 99]
heapq.heappushpop(lst,66)
[3, 5, 5, 9, 6, 66, 8, 99]
'''
最大的n个是谁;
最小的n个是谁;
'''
print(heapq.nlargest(3,lst))
[99, 66, 9]
print(heapq.nsmallest(3,lst))
[3, 5, 5]
'''
合并
'''
lst1 = [100,101]
lst2 = [3, 5, 5, 9, 6, 66, 8, 99]
lst = list(heapq.merge(lst1,lst2))
[3, 5, 5, 9, 6, 66, 8, 99, 100, 101]
https://blog.csdn.net/weixin_42317507/article/details/92801893
python有序列表的维护 - B树和B+树
库函数 : from sortedcontainers import SortedList
大概看了一下SortedList的初始化,和add()方法,发现它可能是用B+树进行维护的。 B+ 树的叶节点中存的是列表,最后维护的数组通过映射实现O(1)时间复杂度的查找。添加元素是O(log2(n))
关于B树和B+树的参考文档
漫画:什么是B+树?: https://zhuanlan.zhihu.com/p/54102723
B树每个结点都存data
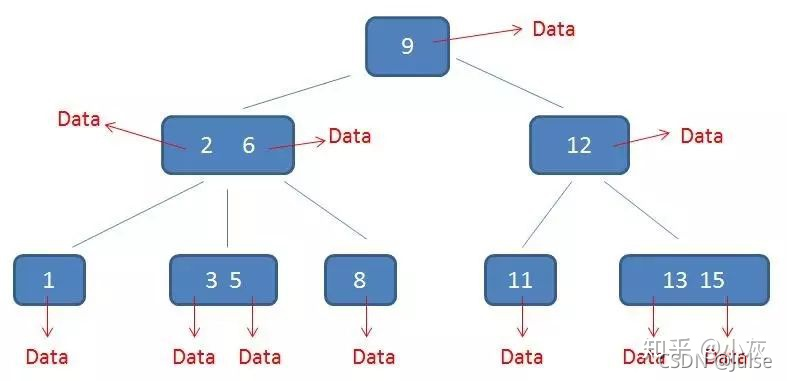
B+树的每个叶节点存data,并且叶节点之间要连接起来
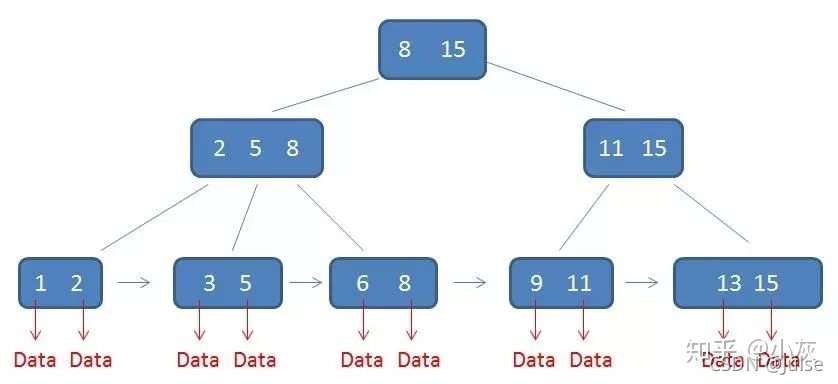
todo:B树和B+树维护的规则弄明白了再来补充