剑指 Offer 32 - II. 从上到下打印二叉树 II
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
提示:
节点总数 <= 1000
迭代实现BFS
广度优先遍历是按层层推进的方式,遍历每一层的节点。题目要求的是返回每一层的节点值,所以这题用广度优先来做非常合适。
广度优先需要用队列作为辅助结构,我们先将根节点放到队列中,然后不断遍历队列。
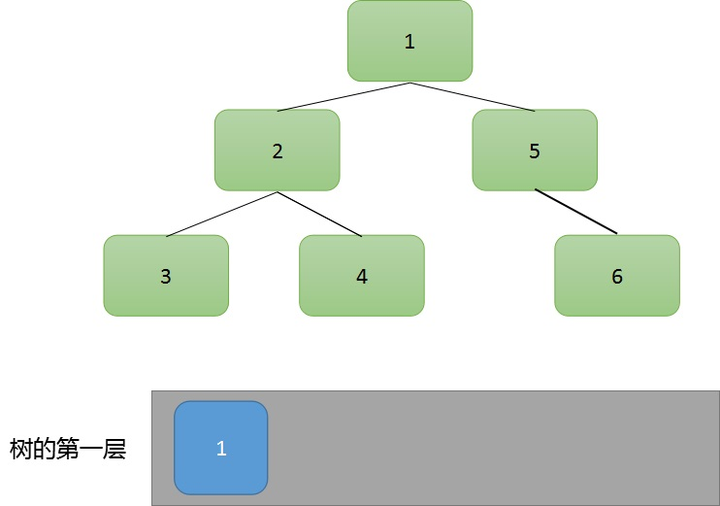
首先拿出根节点,如果左子树/右子树不为空,就将他们放入队列中。第一遍处理完后,根节点已经从队列中拿走了,而根节点的两个孩子已放入队列中了,现在队列中就有两个节点 2 和 5。
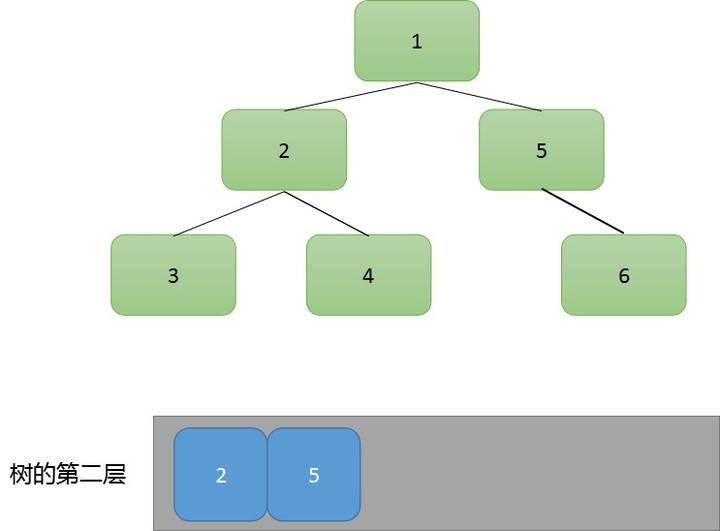
第二次处理,会将 2 和 5 这两个节点从队列中拿走,然后再将 2 和 5 的子节点放入队列中,现在队列中就有三个节点 3,4,6。
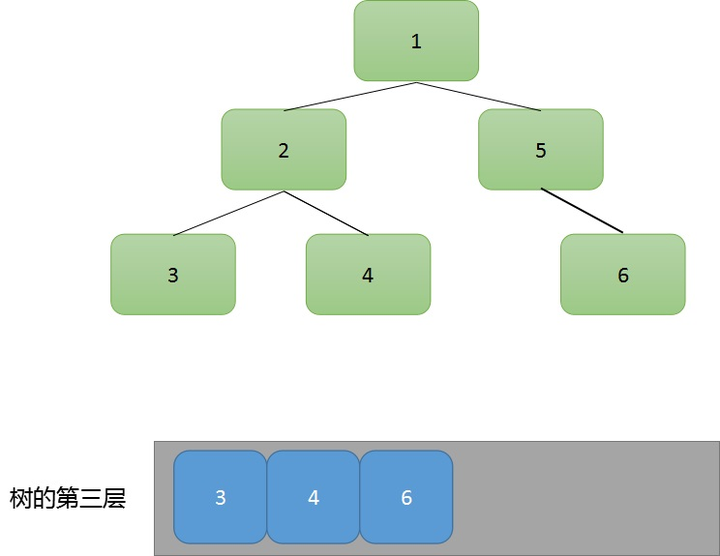
我们把每层遍历到的节点都放入到一个结果集中,最后返回这个结果集就可以了。
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( n ) O(n) O(n)
bfs解法:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if not root:
return[]
res = []
queue = [root]
while queue:
# 获取当前队列的长度,这个长度相当于 当前这一层的节点个数
size = len(queue)
tmp = []
# 将队列中的元素都拿出来(也就是获取这一层的节点),放到临时list中
# 如果节点的左/右子树不为空,也放入队列中
for _ in range(size):
r = queue.pop(0)
tmp.append(r.val)
if r.left:
queue.append(r.left)
if r.right:
queue.append(r.right)
res.append(tmp)
return res
递归实现 DFS
本题使用 DFS 同样能做。由于题目要求每一层的节点都是从左到右遍历,因此递归时也要先递归左子树、再递归右子树。
DFS 做本题的主要问题是: DFS 不是按照层次遍历的,为了让递归的过程中同一层的节点放到同一个列表中,在递归时要记录每个节点的深度 level。递归到新节点要把该节点放入 level 对应列表(res)的末尾。
当遍历到一个新的深度 level,而最终结果 res 中还没有创建 level 对应的列表时,应该在 res 中新建一个列表用来保存该 level 的所有节点。
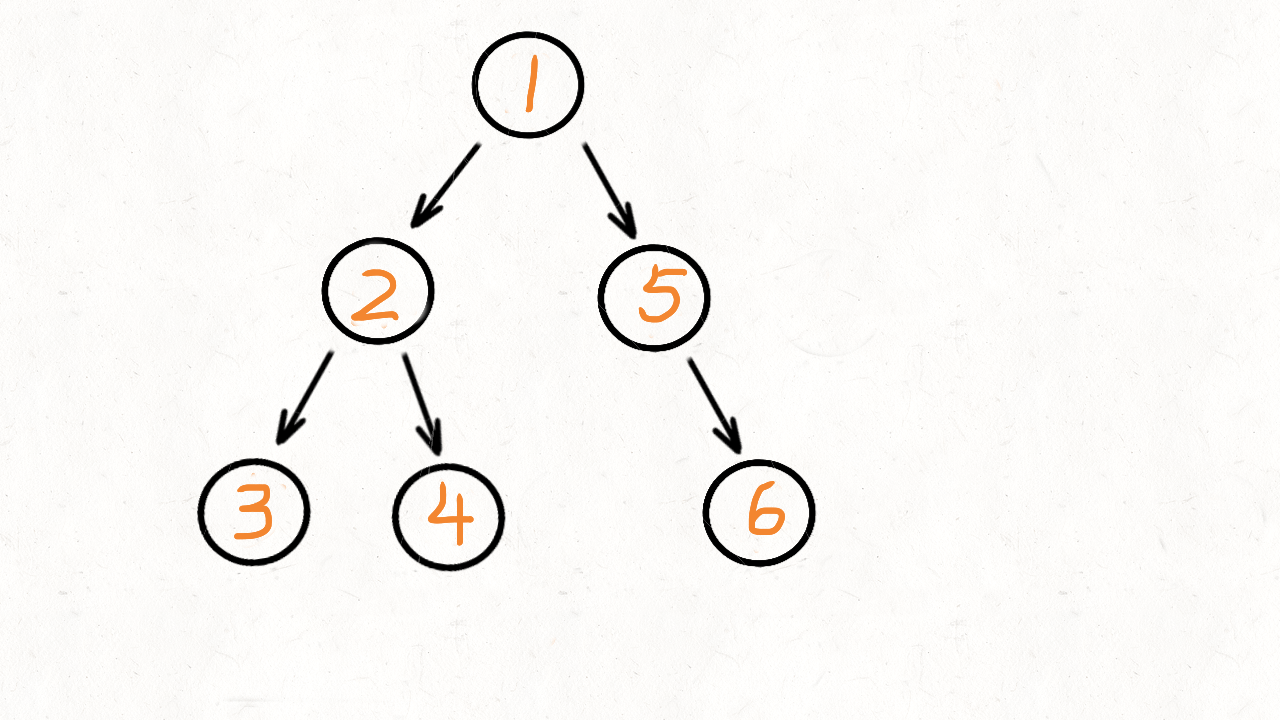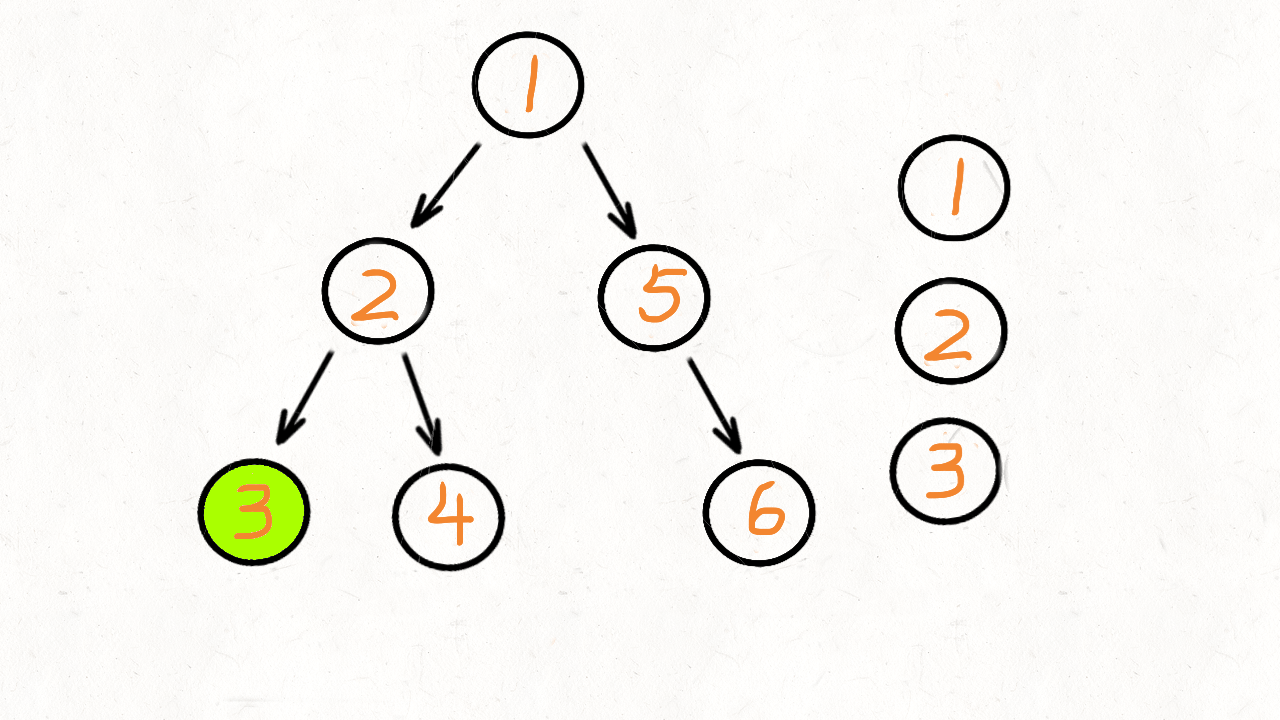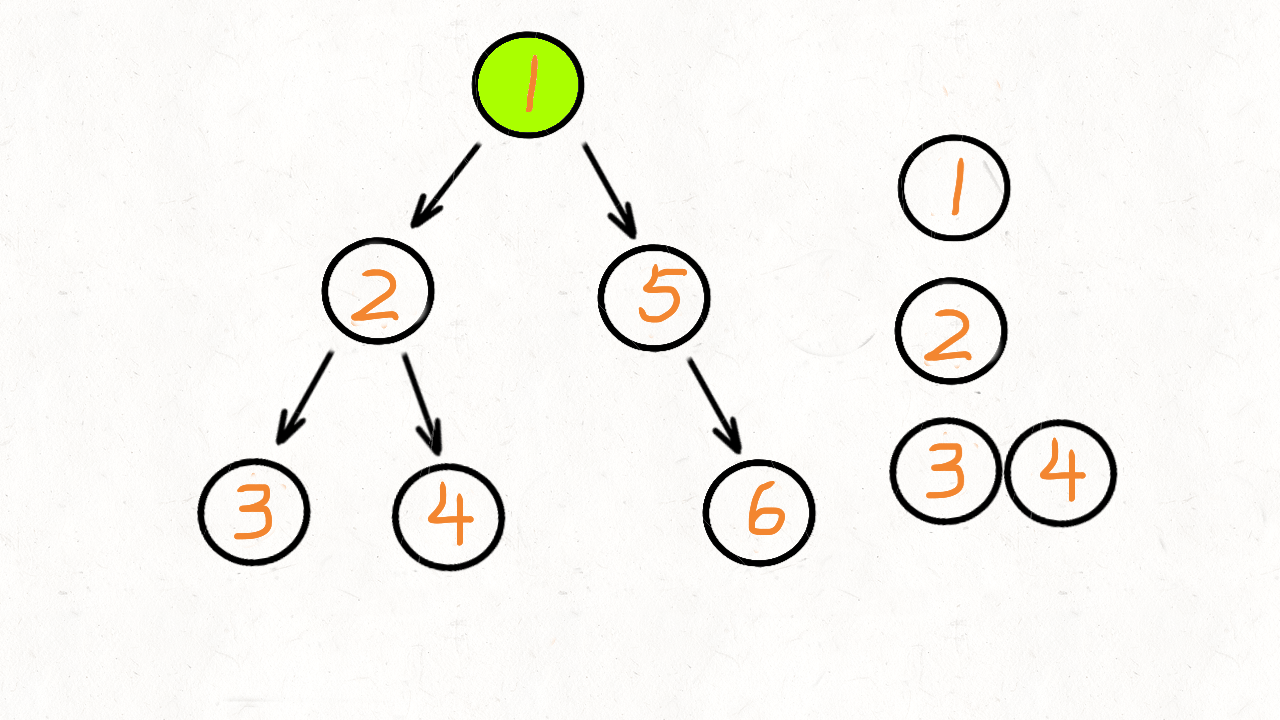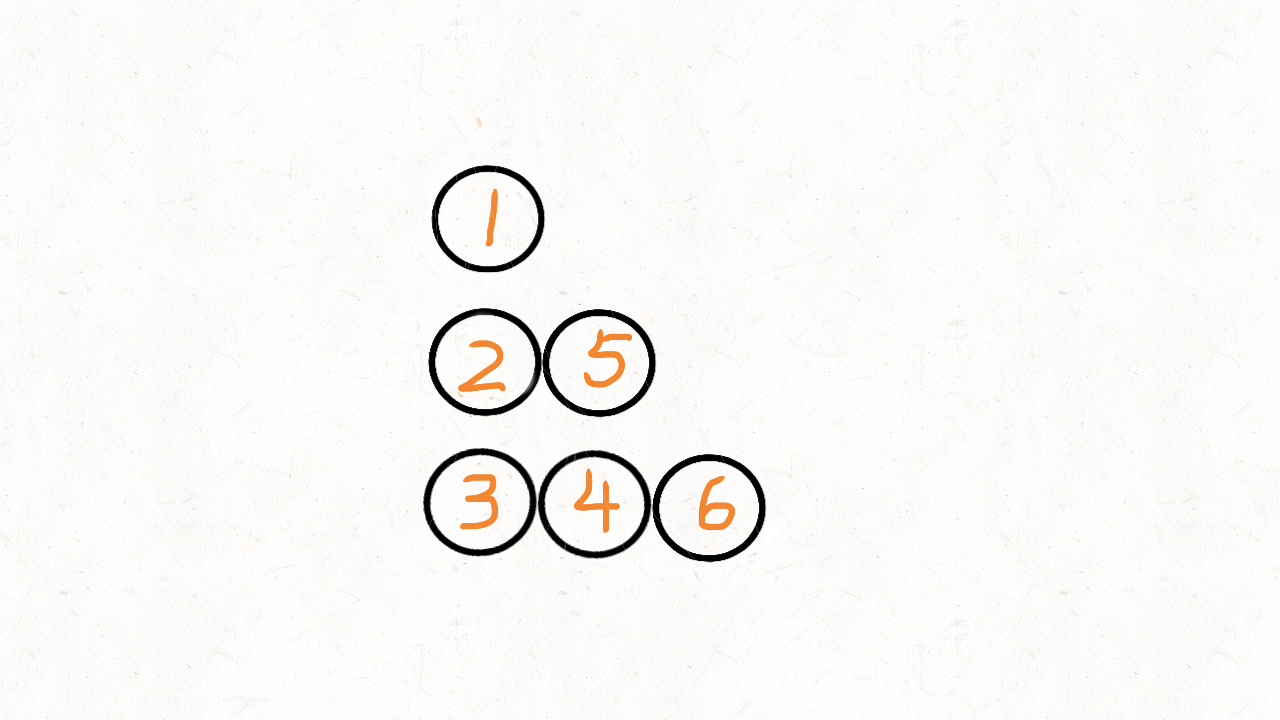
把这个二叉树的样子调整一下,摆成一个田字形的样子。田字形的每一层就对应一个res 。
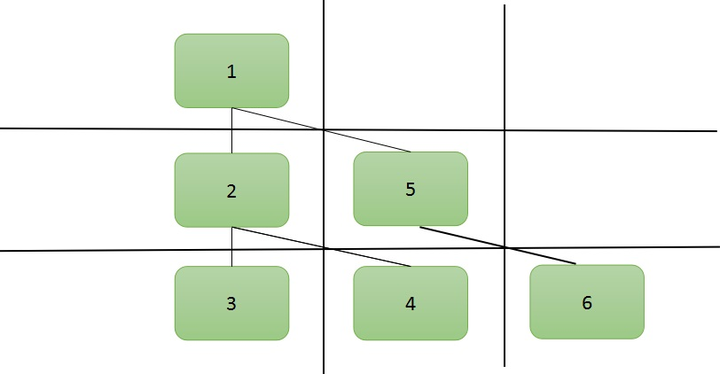
按照深度优先的处理顺序,会先访问节点 1,再访问节点 2,接着是节点 3。
之后是第二列的 4 和 5,最后是第三列的 6。
每次递归的时候都需要带一个 level(表示当前的层数),也就对应那个田字格子中的第几行,如果当前行对应的 res 不存在,就加入一个空 res进去。
动态演示如下:
根节点为第0层:
class Solution(object):
def levelOrder(self, root):
res = []
self.level(root, 0, res)
return res
def level(self, root, level, res):
if not root:
return
if len(res) == level:#只有在新的深度level才会加[],即保证了 res>level
res.append([])
res[level].append(root.val)
if root.left:
self.level(root.left,level+1,res)
if root.right:
self.level(root.right,level+1,res)
根节点为第1层:
class Solution(object):
def levelOrder(self, root):
if not root:
return []
res = []
def dfs(level,r):
# 假设res是[ [1],[2,3] ], level是3,就再插入一个空list放到res中
if len(res) < level:
res.append([])
# 将当前节点的值加入到res中,level代表当前层,假设level是3,节点值是99
# res是[ [1],[2,3] [4] ],加入后res就变为 [ [1],[2,3] [4,99] ]
res[level-1].append(r.val)
if r.left:
dfs(level+1,r.left)
if r.right:
dfs(level+1,r.right)
dfs(1,root)
return res