给定一个正整数、负整数和 0 组成的 N × M?矩阵,编写代码找出元素总和最大的子矩阵。
返回一个数组?[r1, c1, r2, c2](最大子矩阵的和),其中?r1,?c1?分别代表子矩阵左上角的行号和列号,r2,?c2?分别代表右下角的行号和列号。若有多个满足条件的子矩阵,返回任意一个均可。
注意:本题相对书上原题稍作改动
示例:
输入:
[
? [-1,0],
? [0,-1]
]
输出:[0,1,0,1]
解释:输入中标粗的元素即为输出所表示的矩阵
说明:
1 <= matrix.length, matrix[0].length <= 200
?首先使用基础引入:53.最大子序列和
????????在该问题中,数据从一维变成了二维,但实质相同,同样是再求最大子序和,需要将二维转化为一维,对于矩阵的每一列,将其加在一起,成为了一维上的一个数,二维矩阵的和转化为了一维数组的和。
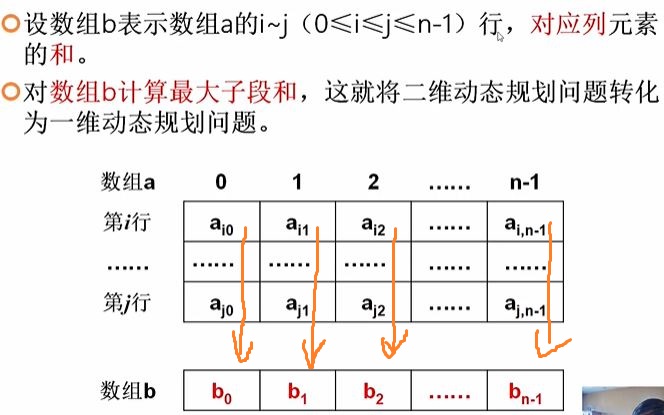
将二维问题转化为了一维问题,现在另一个问题就是怎么把所有情况都遍历到呢?
我们以第i行为第一行,向下延伸,设最后一行为第j行,我们就i在这么一个范围内,将二维问题转化为一维问题,再求解最大子序列和。
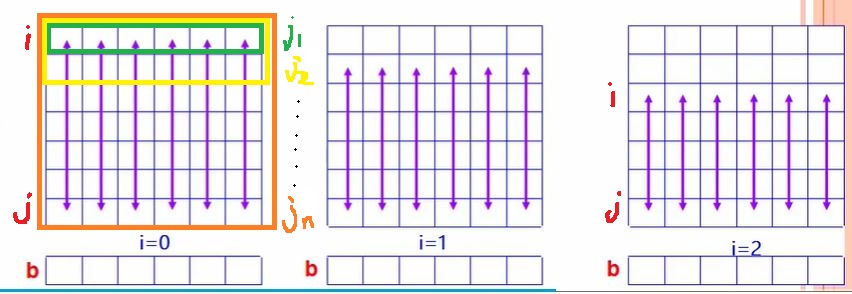
代码实现
import java.util.*;
// 最大子矩阵的和
public class Main1 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[][] matrix = new int[n][m];
for(int i = 0; i < n; i ++) {
for(int j = 0; j < m; j ++) {
matrix[i][j] = sc.nextInt();
}
}
int ans = getMaxSubMatrix(matrix);
System.out.println(ans);
}
private static int getMaxSubMatrix(int[][] matrix) {
// TODO Auto-generated method stub
int n = matrix.length;
int m = matrix[0].length;
int[] indexBE = new int[4];
int[] b = new int[m]; //记录当前i~j行组成大矩阵的每一列的和,将二维转化为一维
int sum = 0; //相当于dp[i],dp_i
int maxSum = Integer.MIN_VALUE; //记录最大值
int rowTemp = 0;
int colTemp = 0;//暂时记录左上角,相当于begin
//以i为上边,从上而下扫描
for(int i = 0; i < n; i ++) {
// 每次更换子矩形上边,就要清空b,重新计算每列的和
for(int t = 0; t < m; t ++) {
b[t] = 0;
}
// 子矩阵的下边,从i到N-1,不断增加子矩阵的高
for(int j = i; j < n; j ++) {
//一下就相当于求一次最大子序列和
sum = 0;//从头开始求dp
for(int k = 0; k < m; k ++) {
b[k] += matrix[j][k];
//我们只是不断增加其高,也就是下移矩阵下边,所有这个矩阵每列的和只需要加上新加的哪一行的元素
//因为我们求dp[i]的时候只需要dp[i-1]和nums[i],所有在我们不断更新b数组时就可以求出当前位置的dp_i
if(sum > 0) {
sum += b[k];
}else {
sum = b[k];
rowTemp = i;
colTemp = k;
}
if(sum > maxSum) {
maxSum = sum;
indexBE[0] = rowTemp;
indexBE[1] = colTemp;
indexBE[2] = j;
indexBE[3] = k;
}
}
}
}
return maxSum;
}
}
/*
3 4
-3 5 -1 5
2 4 -2 4
-1 3 -1 3
*/