[数据结构与算法]Leetcode 285. 二叉搜索树中的中序后继(medium)

题目

给定一棵二叉搜索树和其中的一个节点 p ，找到该节点在树中的中序后继。如果节点没有中序后继，请返回 null 。

节点?p?的后继是值比?p.val?大的节点中键值最小的节点。

示例 1：

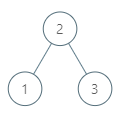
输入：root = [2,1,3], p = 1
输出：2
解释：这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。
示例?2：

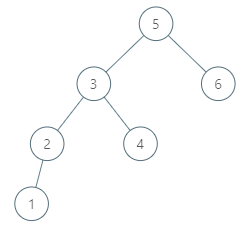
输入：root = [5,3,6,2,4,null,null,1], p = 6
输出：null
解释：因为给出的节点没有中序后继，所以答案就返回 null 了。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/inorder-successor-in-bst
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

1.原始解法

直接对树进行中序遍历，存在列表中。找到p节点在列表中的位置，输入他后一个元素（如果在结尾，返回null）。

结果：通过测试用例，用时72ms，内存使用量19MB

代码：

class Solution:
    def LDRTraverse(self, node, nodes):
        if node.left:
            self.LDRTraverse(node.left, nodes)
        nodes.append(node)
        if node.right:
            self.LDRTraverse(node.right, nodes)

    def inorderSuccessor(self, root: 'TreeNode', p: 'TreeNode') -> 'TreeNode':
        # traverse the tree in LDR order 
        # use a list to store visited nodes
        nodes = []
        self.LDRTraverse(root, nodes)

        i = nodes.index(p)
        if i == len(nodes) - 1:
            return
        else:
            return nodes[i+1]

?2. 第一次优化

其实可以对p进行分类讨论，如果p有右子树，则他的中序后继应该为他的右子树中最小的那个节点。所以我们可以在最开始加一个if判断语句。

结果：通过测试用例，用时52ms（击败100%），内存使用量18.8MB

代码：

class Solution:
    def LDRTraverse(self, node, nodes, p):
        if node.left:
            self.LDRTraverse(node.left, nodes, p)           

        nodes.append(node)
        if node.right:
            self.LDRTraverse(node.right, nodes, p)

    def inorderSuccessor(self, root: 'TreeNode', p: 'TreeNode') -> 'TreeNode':
        if p.right:
            node = p.right
            while node.left:
                node = node.left
            return node        
        else:
            # traverse the tree in LDR order 
            # use a list to store visited nodes
            nodes = []
            self.LDRTraverse(root, nodes, p)

            i = nodes.index(p)
            
            if i == len(nodes) - 1:
                return
            else:
                return nodes[i+1]

3. 后续优化

如果做进一步考量，会发现，当p没有右子树时，我们对整棵树的遍历顺序做了记录，这其实是没有必要的。

假如p是其父节点的左子树，则它的中序后继就是父节点。

假如p是其父节点的右子树，则它的中序后继需要一路向上追溯。这里的代码略有些复杂。

相关知识

1. 二叉搜索树

2. 中序遍历