定义
每个结点最多有两个子树(递归的形式)
特点
二叉树是有向树,有序树
除空二叉树外,每个二叉树都有一个根结点
特殊的二叉树
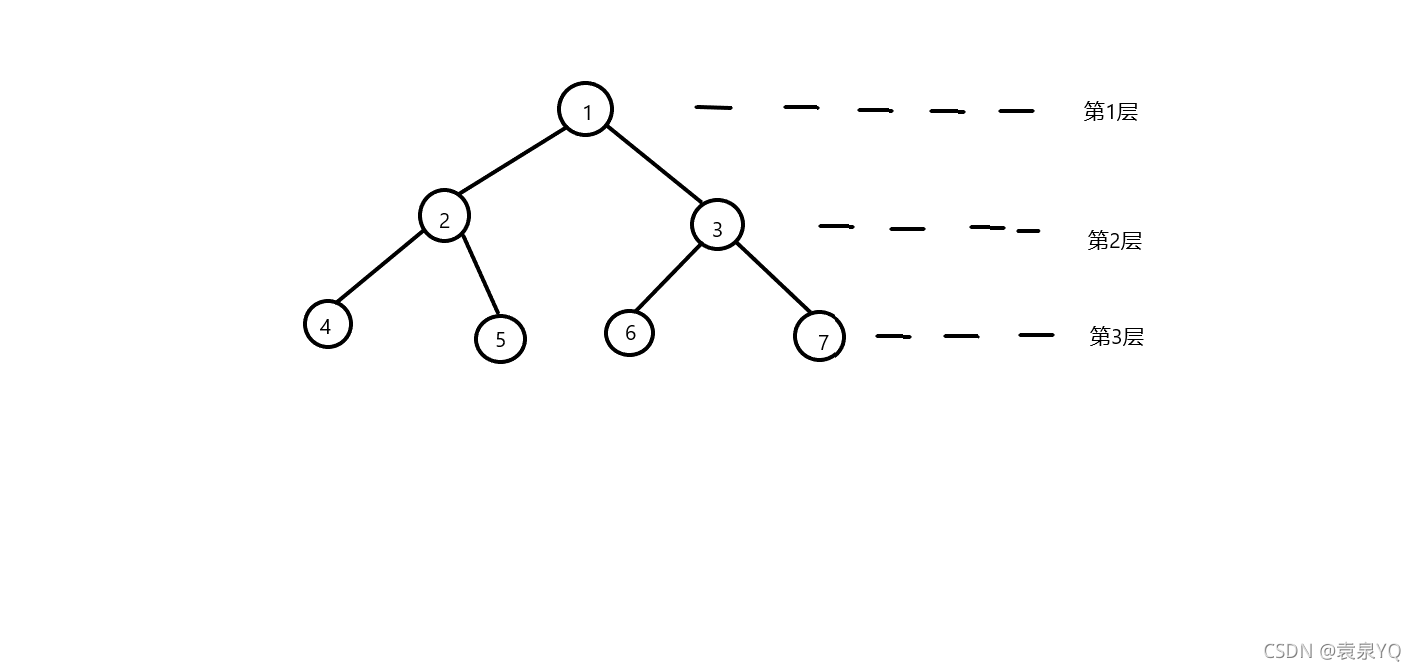
满二叉树
除叶子结点外,其余所有的结点的度均为2(叶子结点度为0)
有h层(树的高度为h),结点个数有2^h - 1个
若从上到下,从左向右依次对满二叉树的结点进行标号,那么结点 i 的左孩子编号为 2i ,右孩子的标号为 2i+1(前提是存在左,右孩子),双亲结点编号为 [ i/2] (取整)
满二叉树的结点只与树的深度有关
完全二叉树
在满二叉树中,从后向前不间断的去掉几个结点(存在度为0,1,2的结点)
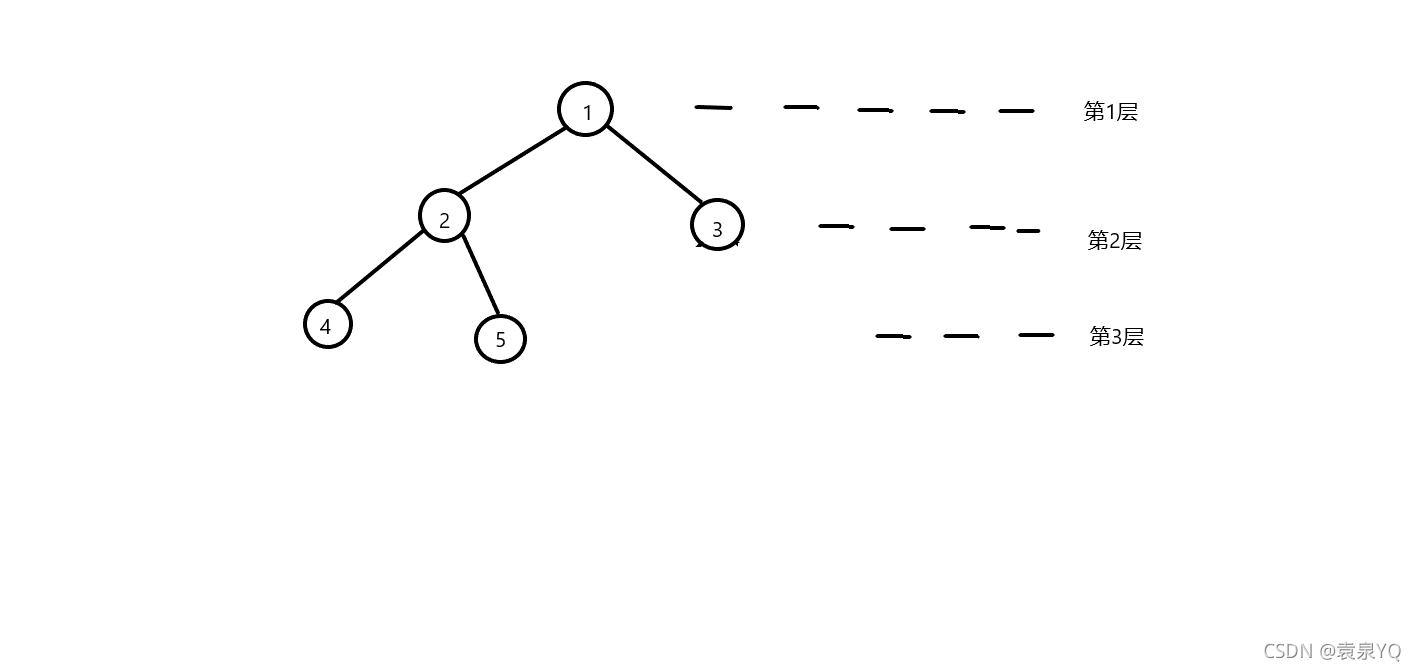
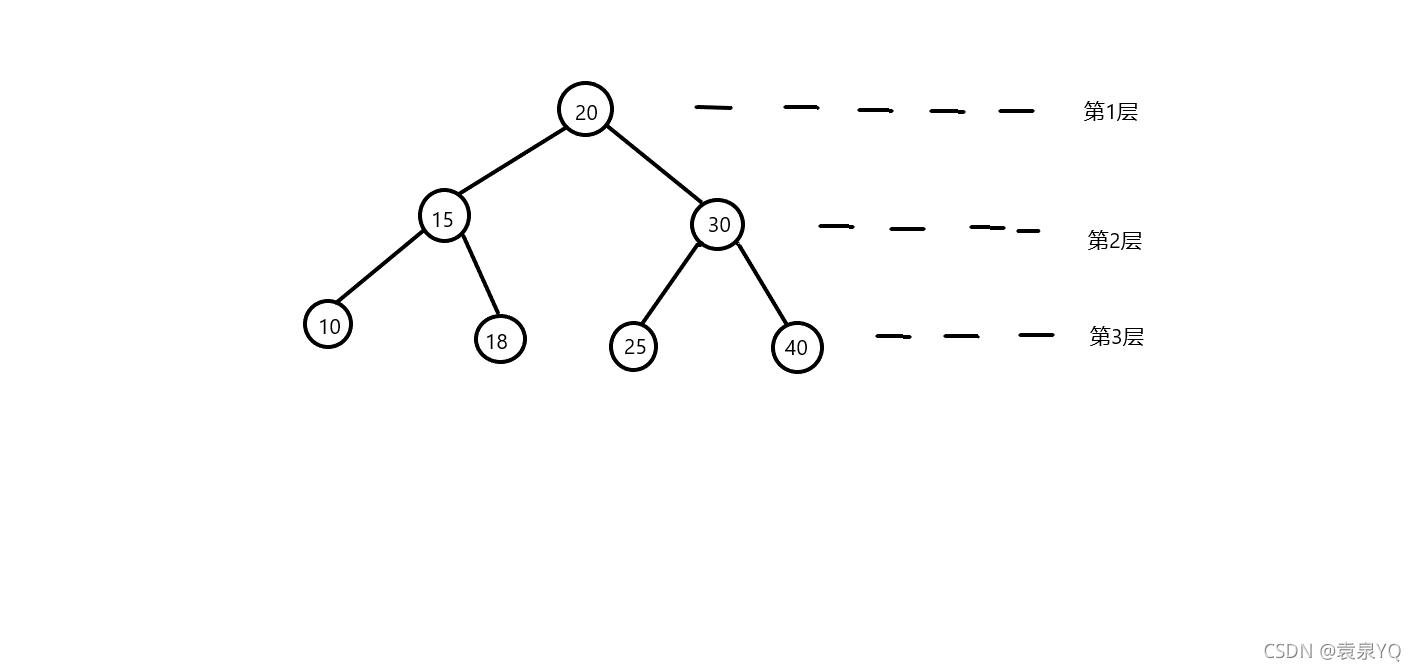
二叉排序树
左子树上的关键字 < 根结点上的关键字 < 右子树上的关键字 (左 < 根 < 右)
其中左子树,右子树也是二叉排序树
二叉树的遍历
(先,中,后是相对根结点而言)
遍历规则是递归规则
以上图的二叉排序树为例
先序遍历
先访问根结点,再遍历左子树,再遍历右子树。(其中左右子树的遍历也要满足“根-左-右”的遍历规则)
遍历结果为:20-15-10-18-30-25-40
中序遍历
先遍历左子树,再访问根结点,再遍历右子树
遍历结果为:10-15-18-20-25-30-40
后序遍历
先遍历左子树,再遍历右子树,再访问根结点
遍历结果为:10-18-15-25-40-30-20