[数据结构与算法]剑指 Offer 55 - I. 二叉树的深度

剑指 Offer 55 - I. 二叉树的深度

输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

例如：

给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7

返回它的最大深度 3 。

递归

很多二叉树的题目，用递归写起来就非常简单，这道题就是。

如果我们知道了左子树和右子树的最大深度 $l$ 和 $r$ ，那么该二叉树的最大深度即为
$$\max (l,r)+1$$
而左子树和右子树的最大深度又可以以同样的方式进行计算。

再来分析下递归的两个条件

1. 递归终止条件：当节点为空时返回
2. 再次递归计算 max( 左节点最大高度，右节点最大高度)+1

终止条件很好理解，节点为空了，就返回0，也就是高度为0。关键是第二句，这句可能不好理解。

我们看下面这个图，假设节点左边节点这一坨的高度是$x$，右边节点那一坨的高度是$y$

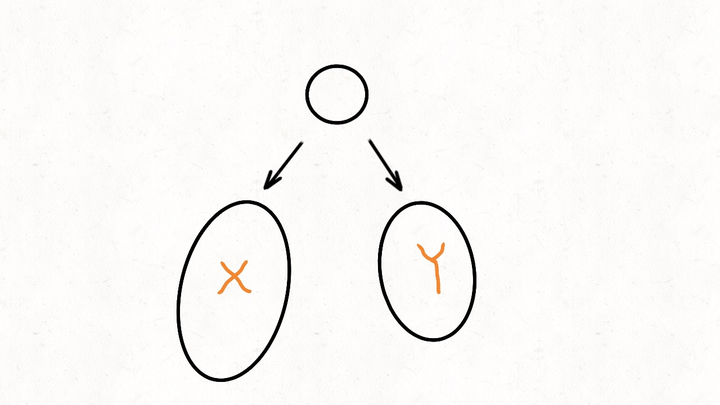
我们需要比较X和Y的值谁大，也就是谁的高度更高，假设X这一坨更高。当我们得到了X的值后，还需要 +1。

+1的原因是，我们只得到了X的高度，但是整个树是由根节点，一坨X和一坨Y组成的。所以为了求得整个树的高度，还需要在X的基础上，再加上1，也就**多加一个节点(**根节点)。

动画演示：

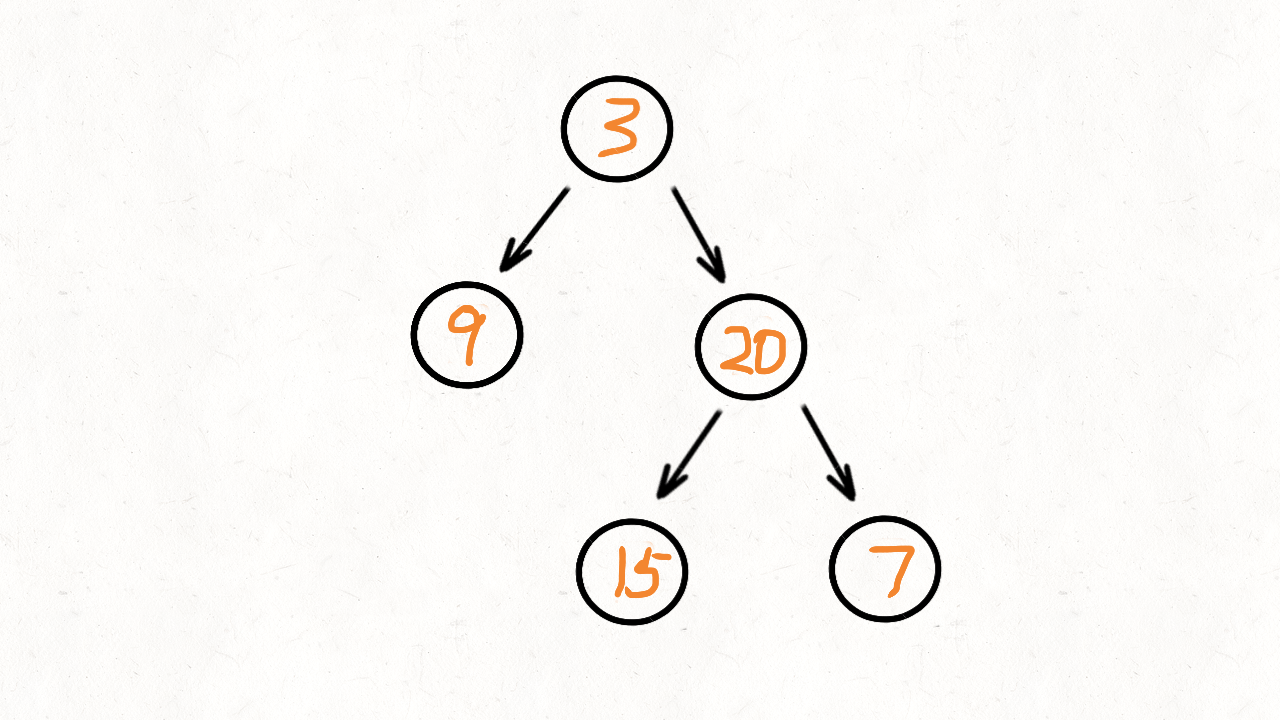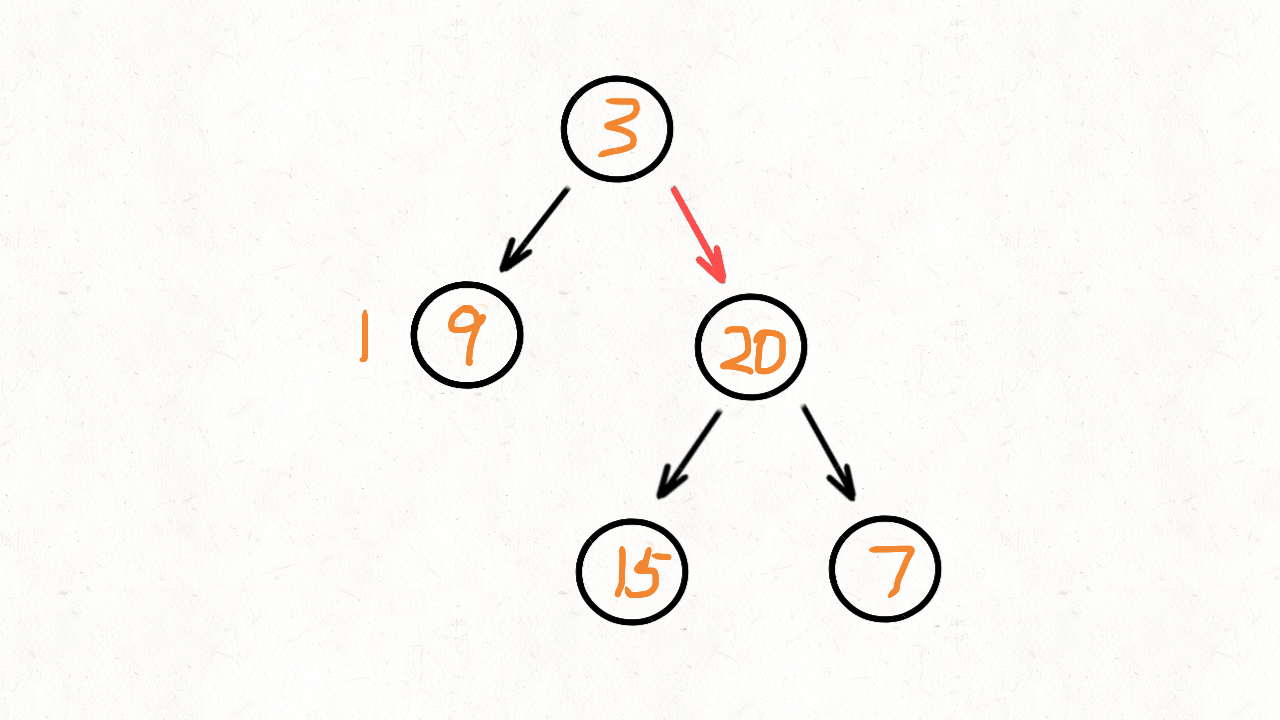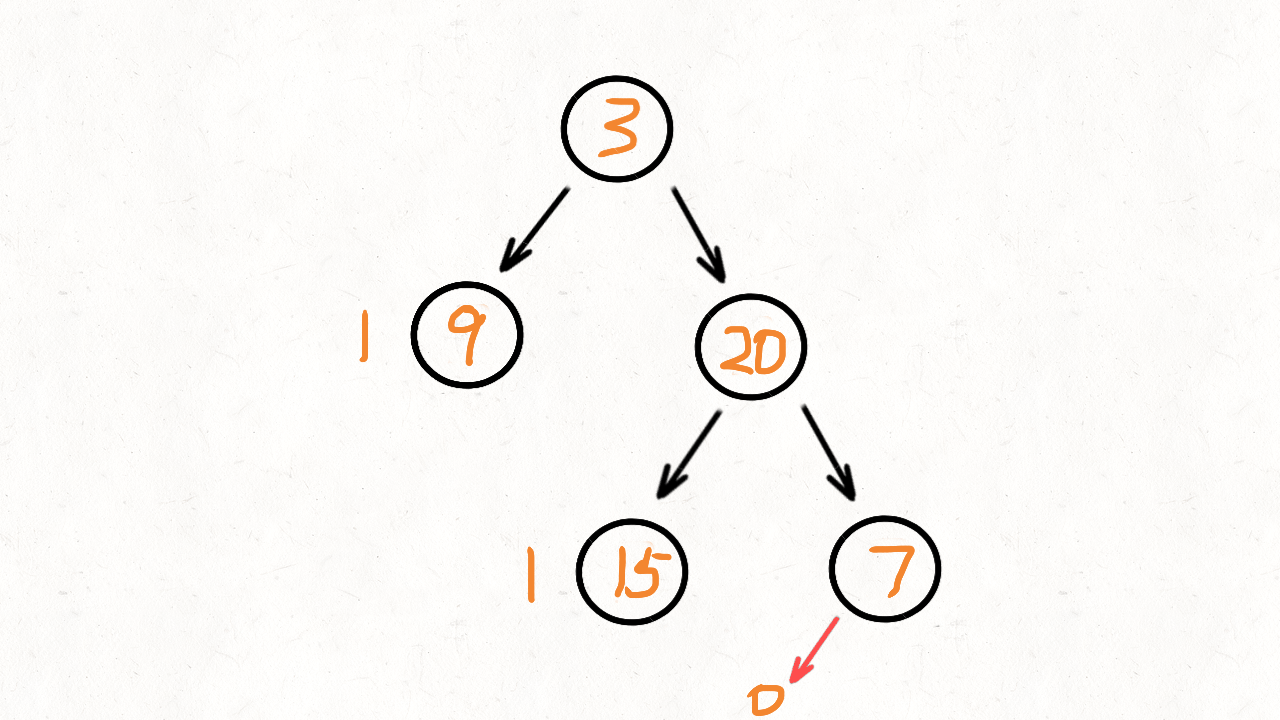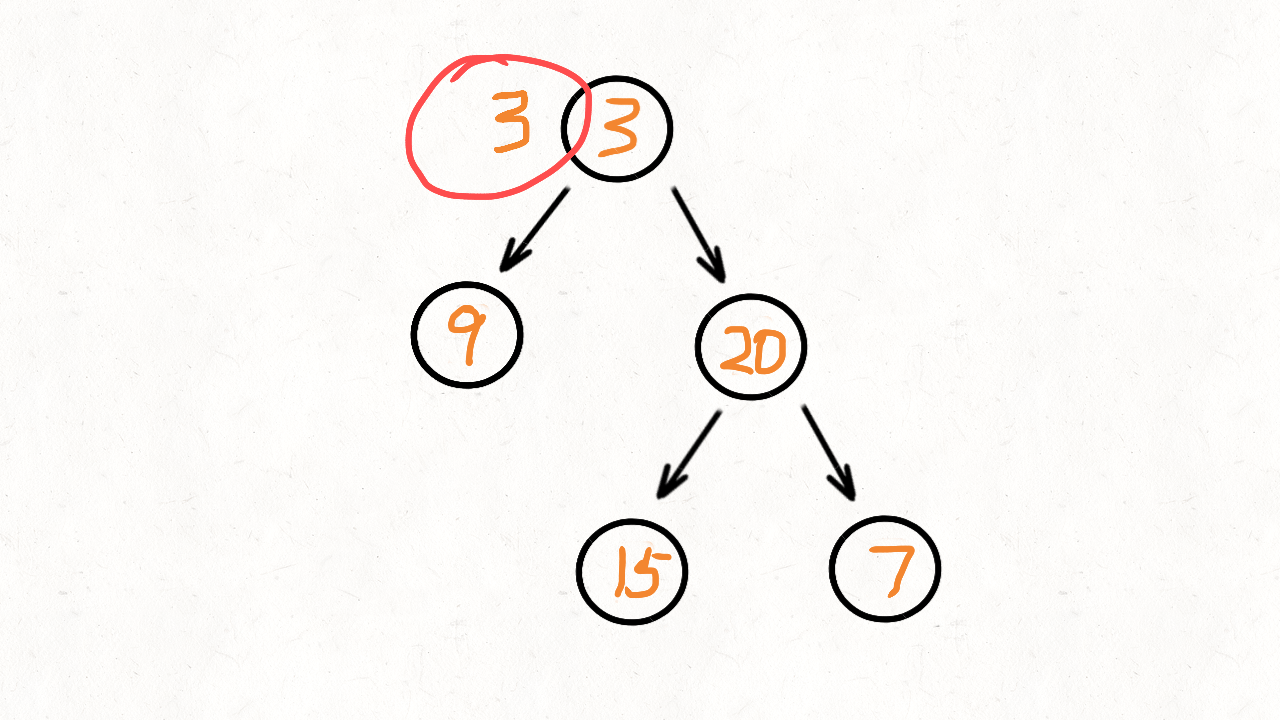
代码实现：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:
            return 0
        else:
            left_height = self.maxDepth(root.left)
            right_height = self.maxDepth(root.right)
            return max(left_height,right_height) +1

迭代实现

DFS实现，从上往下遍历，然后求得最深的一个节点的高度，就是整个树的高度了。

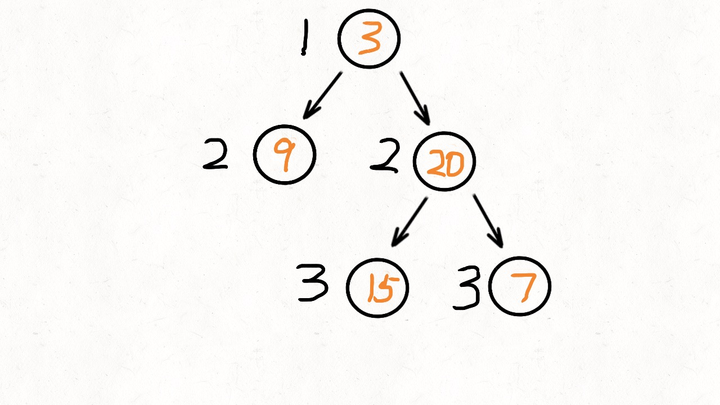
上图中，我们假设每个节点都有一个附加参数key，key就是节点的高度，当遍历完整个树后，就可以求得最大的那个key了。

动画演示：

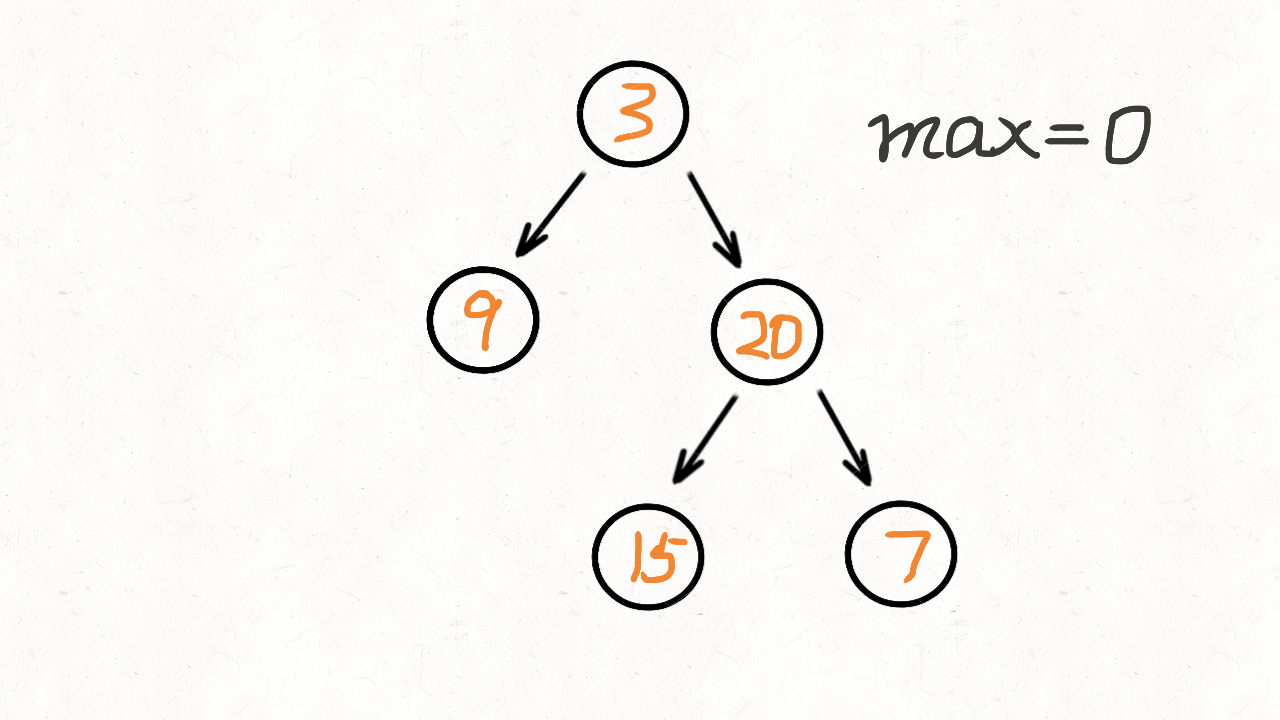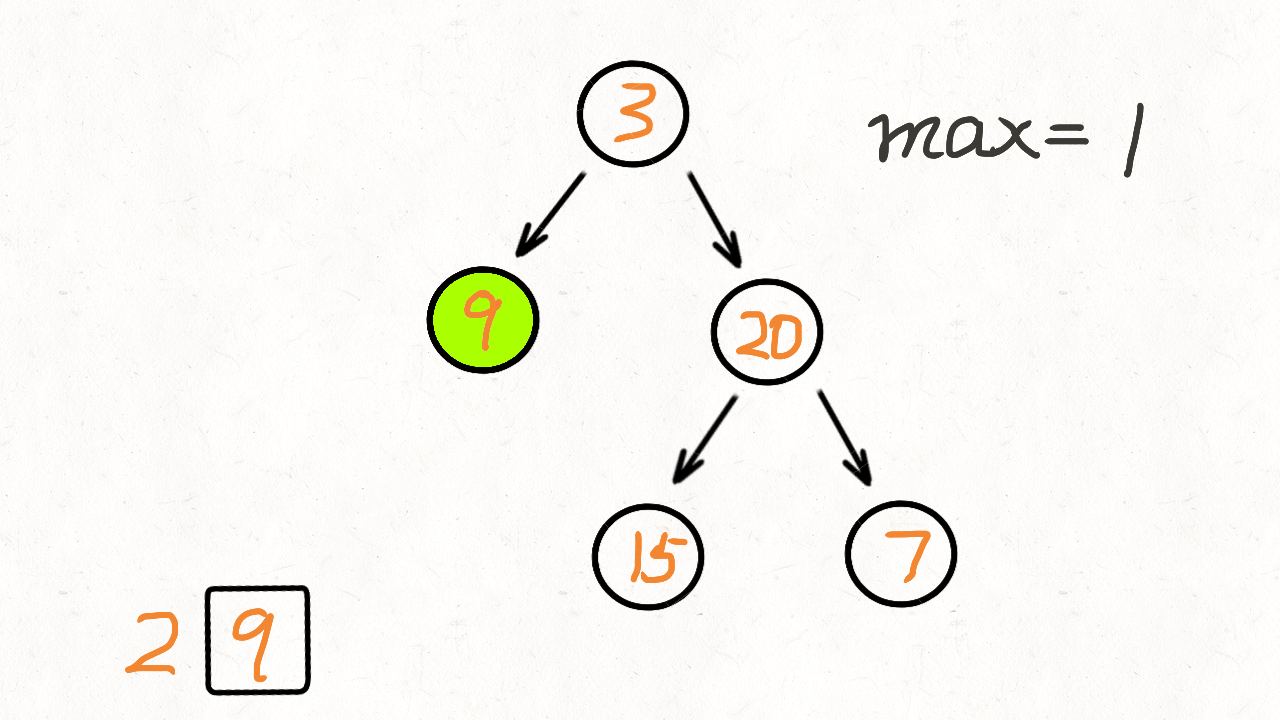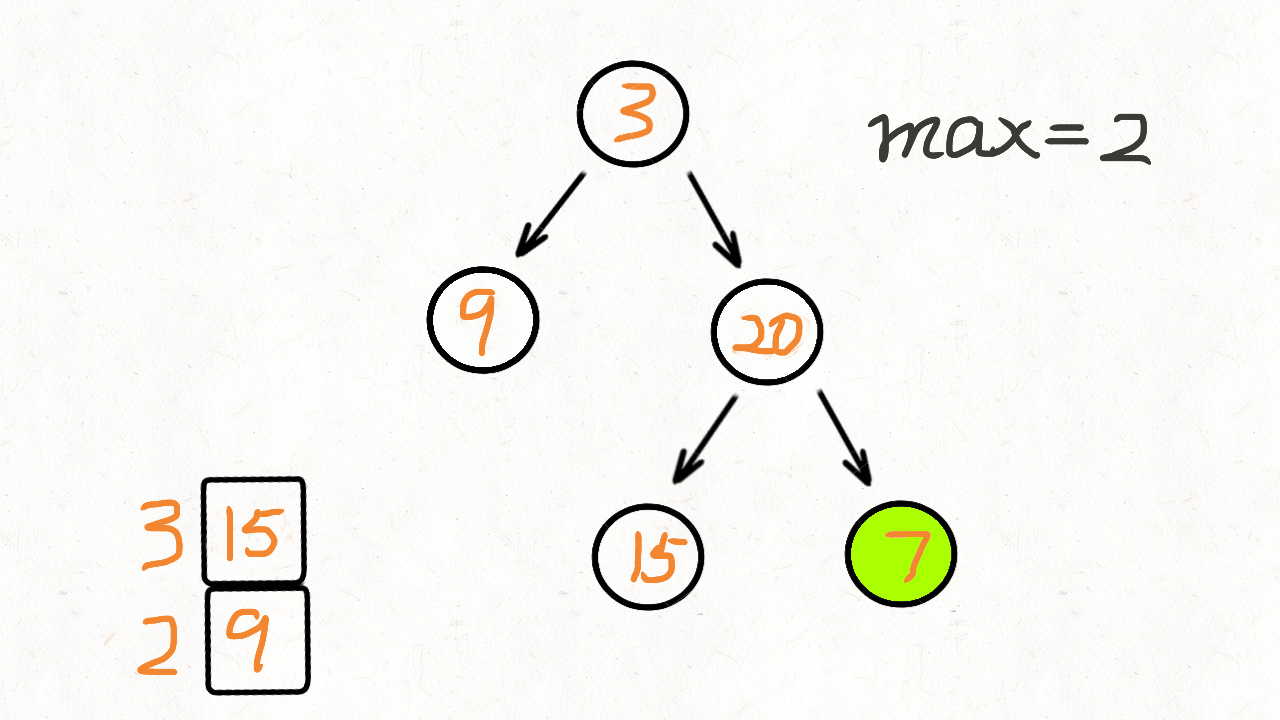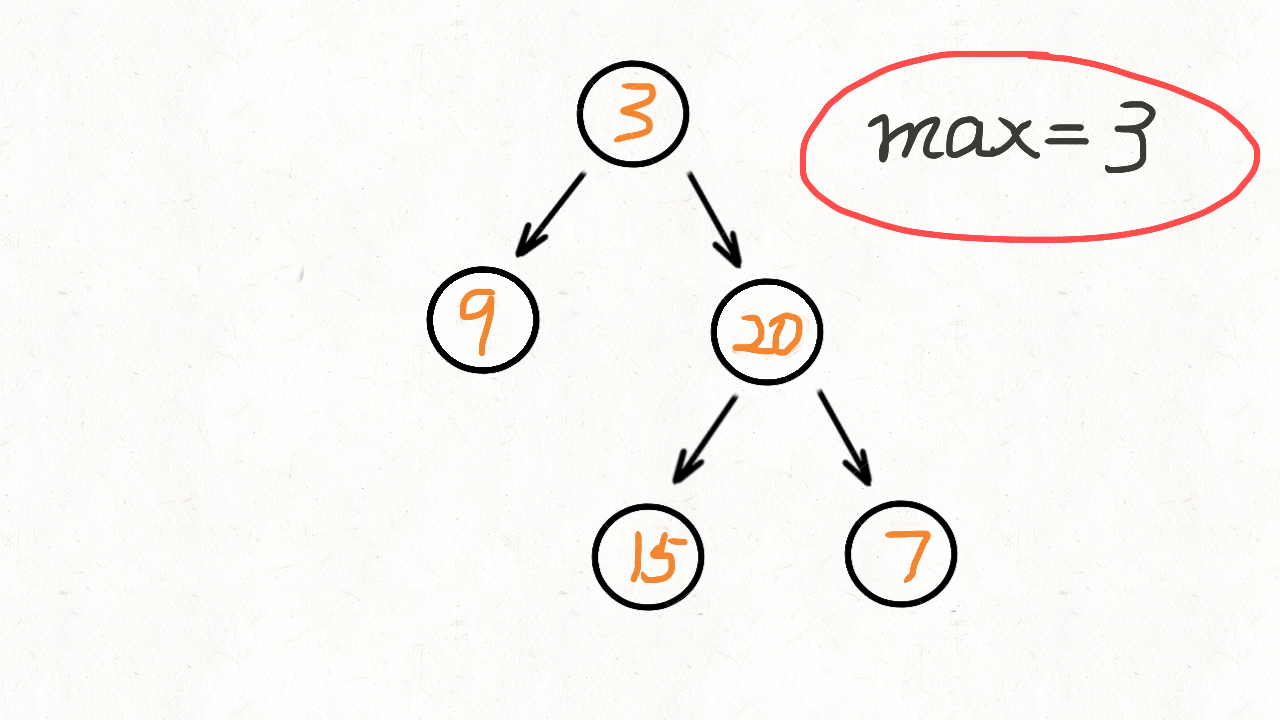
DFS实现，从上往下遍历，得到最大的路径的深度，用栈实现（后进先出）

DFS与BFS有两点不同：

1. 最后得到的深度不一定是最大深度，所以要用max判断（有多条从上往下的路径）
2. DFS（先序遍历）节点右孩子先入栈，左孩子再入栈

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:
            return 0
        stack = [(1,root)]
        depth = 0
        while stack:
            cur_dep, node = stack.pop()
            depth = max(depth,cur_dep)
            if node.right:
                stack.append((cur_dep +1 , node.right))
            if node.left:
                stack.append((cur_dep + 1, node.left))#后进先出
        return depth

还可以是BFS实现，就是每一层从左到右扫描节点，每层节点都扫描完了再进入下一层，用队列实现（先进先出）

class Solution(object):
    def maxDepth(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        if root is None:
            return 0
        queue = [(1, root)]
        while queue:
            depth, node = queue.pop(0)#先进先出
            if node.left:
                queue.append((depth+1,node.left))
            if node.right:
                queue.append((depth+1,node.right))
        return depth

参考

Krahets - 力扣（LeetCode） (leetcode-cn.com)