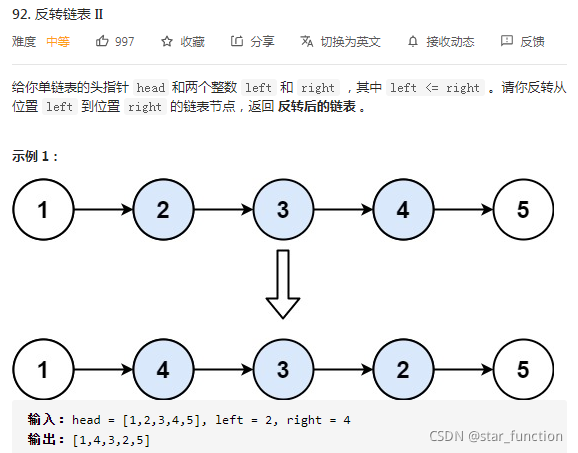
反转链表的局部是反转整个链表的进阶题目。同样,也可以采用递归和迭代两种方法解题。递归实现较为简洁,迭代实现需要注意细节。
1. 递归法
算法时间复杂度为 O(n), 空间复杂度为 O(n)。
递归法需要明确基础条件:当 left == 1时,反转区间 [left, right] 中的结点相当于反转前 right 个结点。
递归的较小规模问题:reverseBetween(head->next, left-1, right-1)。
之后将头结点 head 与 reverseBetween(head->next, left-1, right-1) 的返回值相连接,即可完成反转部分链表。
1.1 思路
那么问题来了,如何反转前 n 个结点呢?
依旧使用迭代法来解决这个问题。
首先来看递归的效果
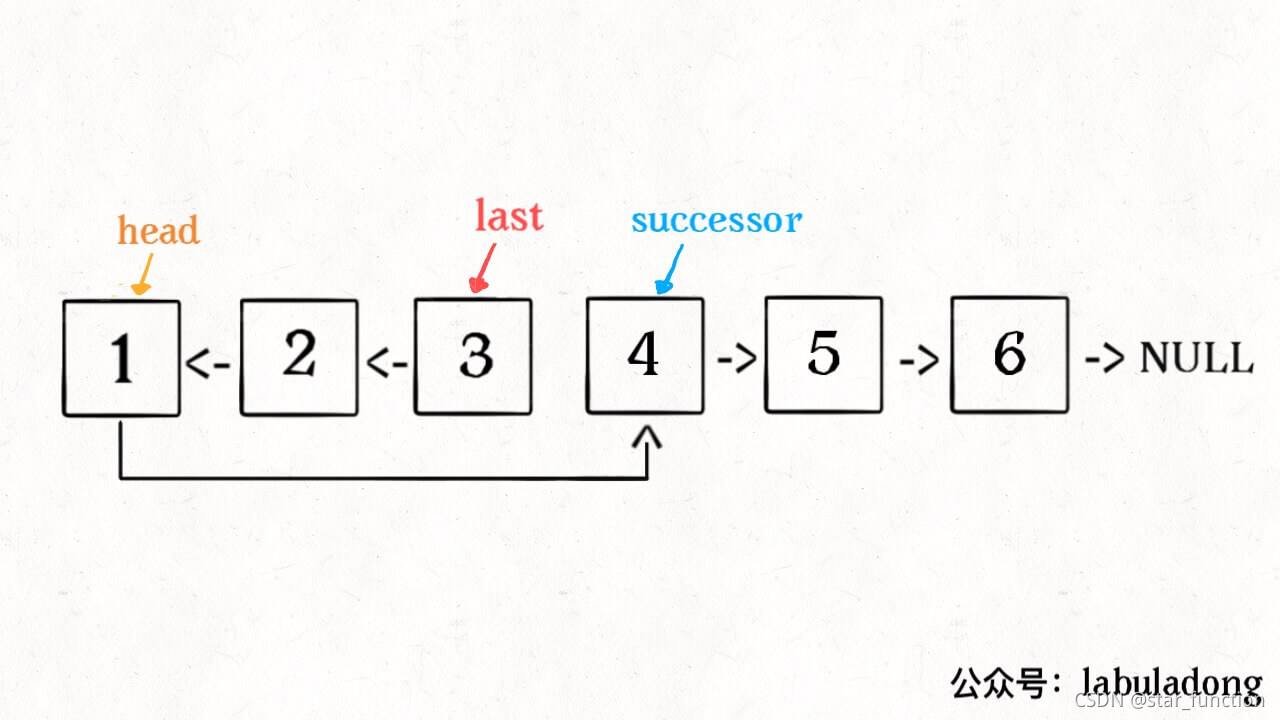
递归的基础条件:n == 1 时,直接返回 head。并记录后驱结点 nxt,方便前 n 个结点反转后连入原有链表。
递归的较小规模问题:reverseN(head->next, n - 1),返回新的头结点 last。
最后将 head 结点反转,连接 reverseN(head->next, n - 1) 后的尾结点。
这与反转整个链表的解法相同。
前 n 个结点反转后,还要与后驱结点 nxt 连接,连入原有链表。
1.2 代码实现
实现过程中需要注意,记录后驱结点 nxt。初始化 ListNode* nxt = NULL; 要在函数外面,我就犯了这个错,导致 nxt 一直指向空指针,nxt->next 报错。
ListNode* nxt = NULL;
ListNode* reverseN(ListNode* head, int n)
{
if(n == 1)
{
nxt = head->next;
return head;
}
ListNode* last = reverseN(head->next, n - 1);
head->next->next = head;
head->next = nxt;
return last;
}
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
if(left == 1)
{
return reverseN(head, right);
}
else
{
head->next = reverseBetween(head->next, left-1, right-1);
}
return head;
}
};
2. 迭代法
算法时间复杂度为 O(n),算法的空间复杂度为 O(1)。
- 迭代法需要遍历反转区间的所有结点,
- 并将反转后的区间链表与原有链表相连接。
这里还用到了虚拟头结点 dummy,哨兵法。
2.1 思路
如图所示,黄色部分是需要反转的区间。具体的步骤如下:
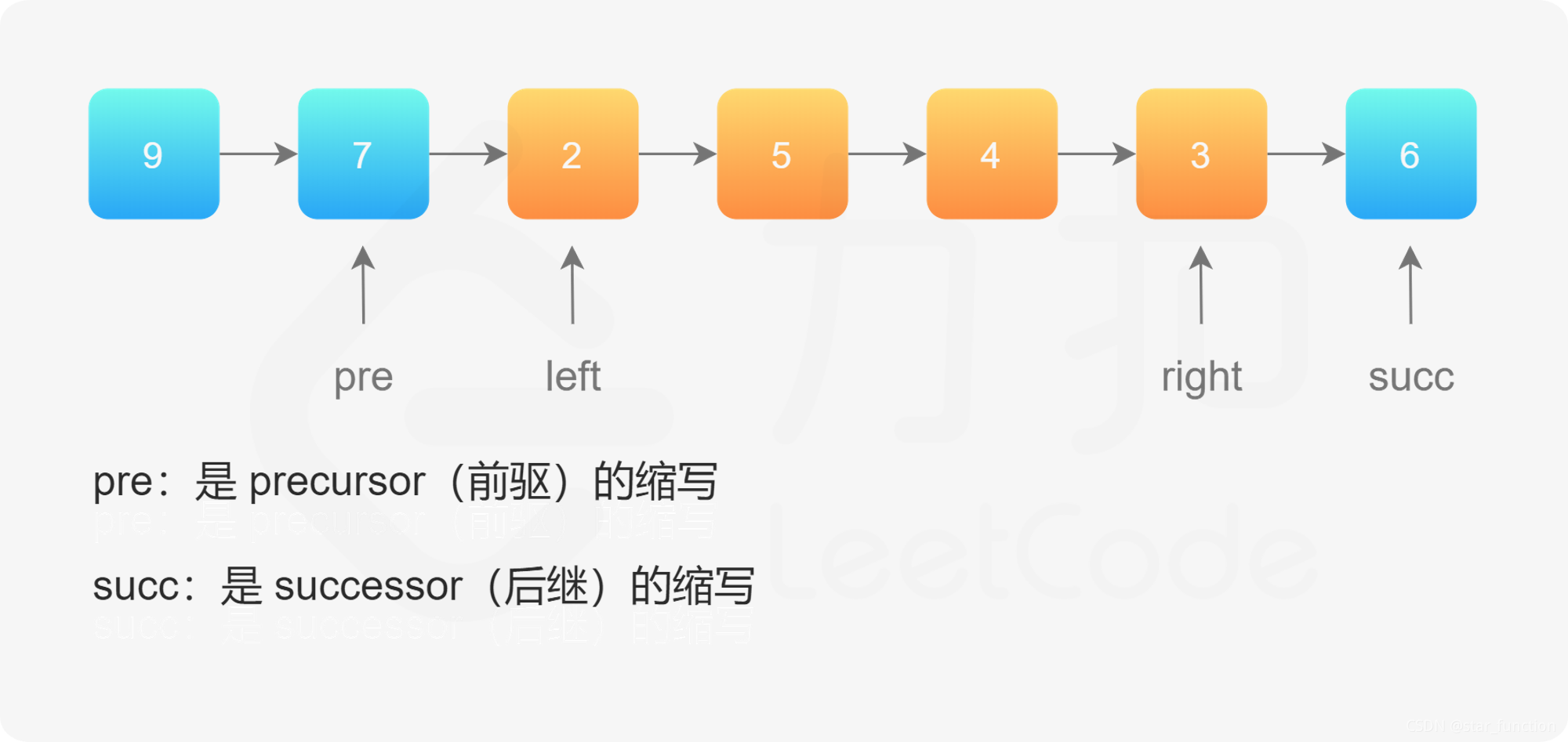
- 首先需要确定链表中 left 和 right 位置的结点
- 并记录 left 的前驱结点和 right 的后继结点位置
- 将 left 和 right 之间的链表截取出来
- 对 left 和 right 间的结点进行反转
- 将反转后的区间链表连入原有链表
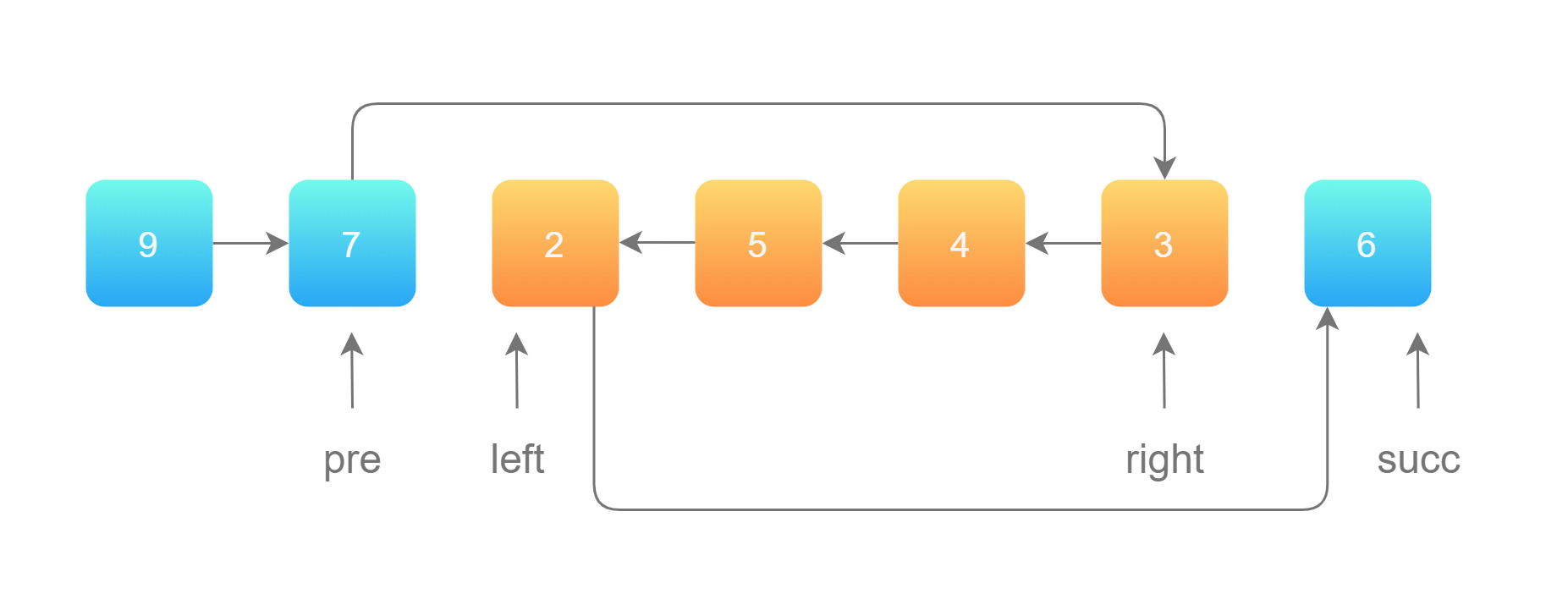
2.2 代码实现
这次使用迭代法实现整个链表的反转 reverseLink。创建一个虚拟结点 dummy 来避免由于 head 发生变化需要分类讨论的情况,dummy 的后驱为 head。
建议使用 for 循环查找 left 、right 结点
void reverseLink(ListNode* head)
{
ListNode* pre = NULL;
ListNode* cur = head;
while(cur != NULL)
{
ListNode* nxt = cur->next;
cur->next = pre;
pre = cur;
cur = nxt;
}
}
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
ListNode* dummy = new ListNode(0);
dummy->next = head;
ListNode* pre = dummy;
//1. 确定 left 的前一个结点 pre,dummy 后移 left - 1 步
for(int i = 0; i < left - 1; i++)
{
pre = pre->next;
}
ListNode* rightnode = pre;
//2. 确定 right 位置的结点,pre 结点后移 right - left + 1 步
for(int i = 0; i < right - left + 1; i++)
{
rightnode = rightnode->next;
}
//3. 截取区间
ListNode* leftnode = pre->next;
ListNode* cur = rightnode->next;
//4. 断开连接
pre->next = NULL;
rightnode->next = NULL;
//5. 反转区间
reverseLink(leftnode);
//6. 连接到原有链表
pre->next = rightnode;
leftnode->next = cur;
return dummy->next;
}
};