2-3树
定义: 2-3树是最简单的B-树(或-树)结构,其每个非叶节点都有两个或三个子女,而且所有叶都在统一层上。2-3树不是二叉树,其节点可拥有3个孩子。不过,2-3树与满二叉树相似。若某棵2-3树不包含3-节点,则看上去像满二叉树,其所有内部节点都可有两个孩子,所有的叶子都在同一级别。另一方面,2-3树的一个内部节点确实有3个孩子,故比相同高度的满二叉树的节点更多。高为h的2-3树包含的节点数大于等于高度为h的满二叉树的节点数,即至少有2^h-1个节点。换一个角度分析,包含n的节点的2-3树的高度不大于log2(n+1)
- 即有二节点又有三节点的平衡二叉树。是一种绝对平衡的树,对学习红黑树有很大的帮助,2-3和红黑树是等价的。
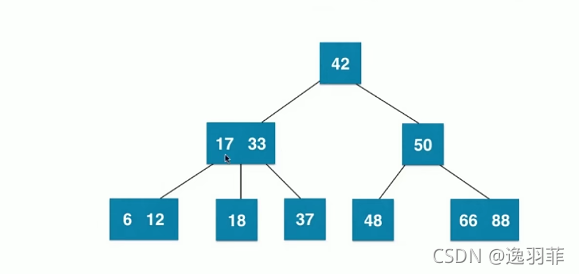
- 如何维持绝对平衡
先插入42

再插入37,**2-3树将永远不会添加到一个空的位置。**因为42的左子树为空,所以不能添加,将会添加到他的父亲节点上,也就是42,于是和42融合。

再插入12,因为2-3树将永远不会添加到一个空的位置,所以暂时先和父亲节点融合。
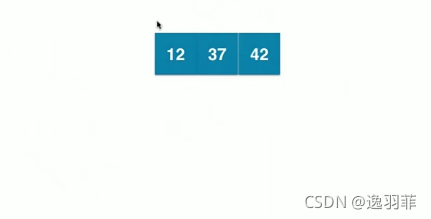
也就是这个样子
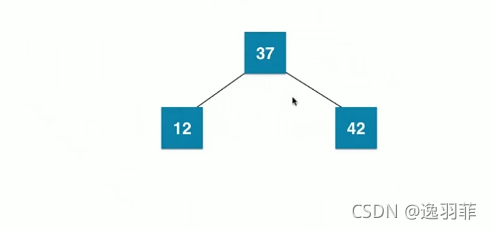
再添加一个节点18 ,因为18小于37,所以要添加到左子树中,比12大,所以要添加到12的右子树中,但是12的右子树是空的,根据定义,2-3树将永远不会添加到一个空的位置,而是要和最后要找的节点进行融合,所以进行融合。如下如:
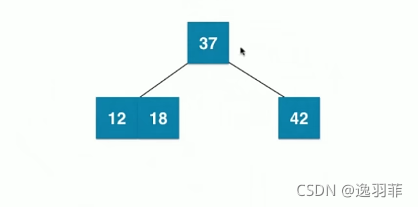
再添加一个节点6,根据以上定义,添加后的图示如下:
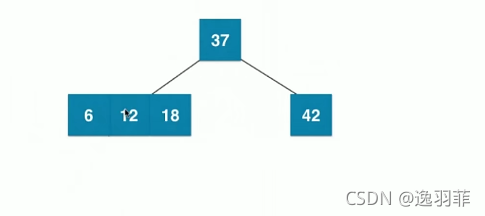
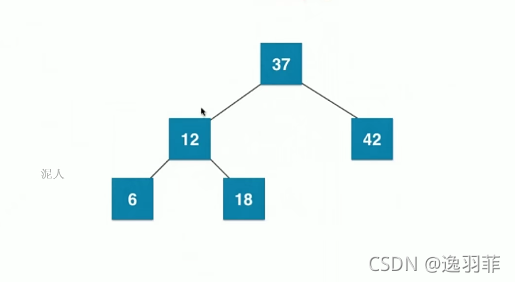
他不是一个绝对平衡的树,然后他将进行拆解。如果叶子节点本身就是3节点,再加上父亲节点是4节点,将会进行融合
12将会和37进行融合
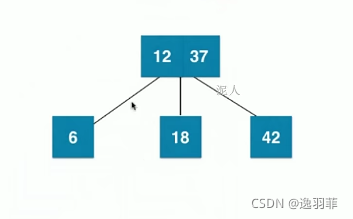
如果再插入11
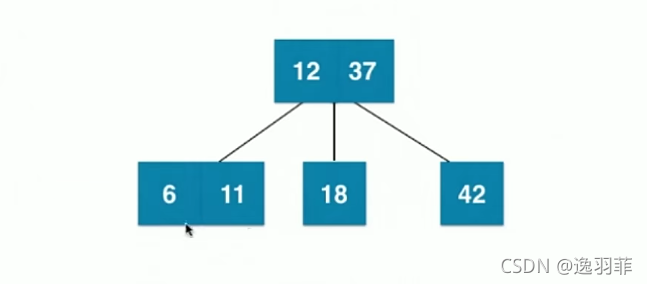
再插入5
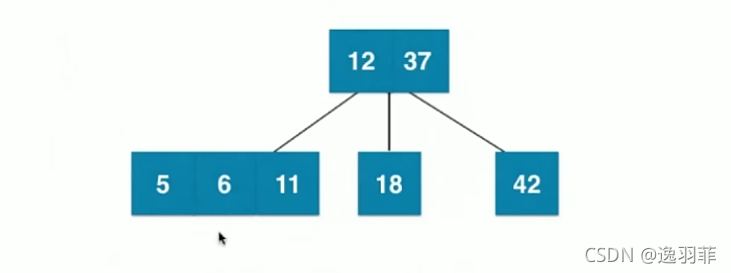
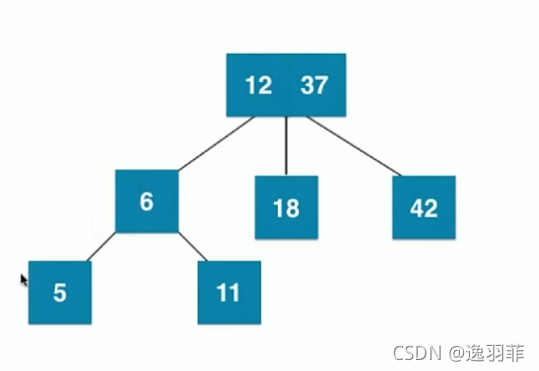
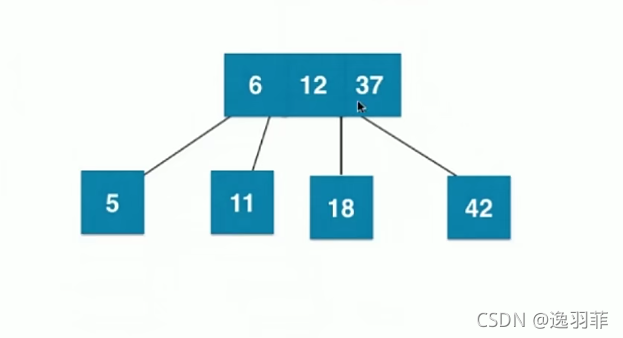
因为最多只能有3个叉,所以以上还会进行分裂,如下
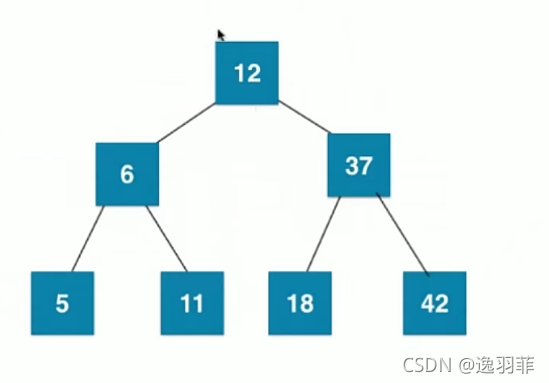
总结

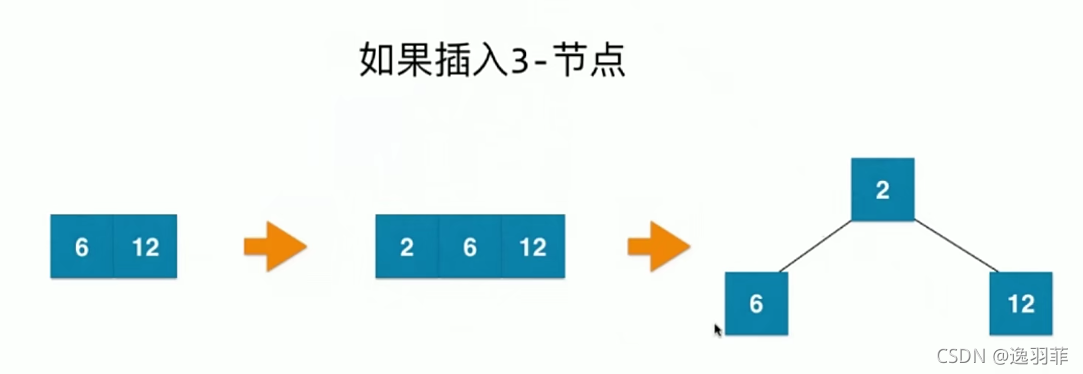
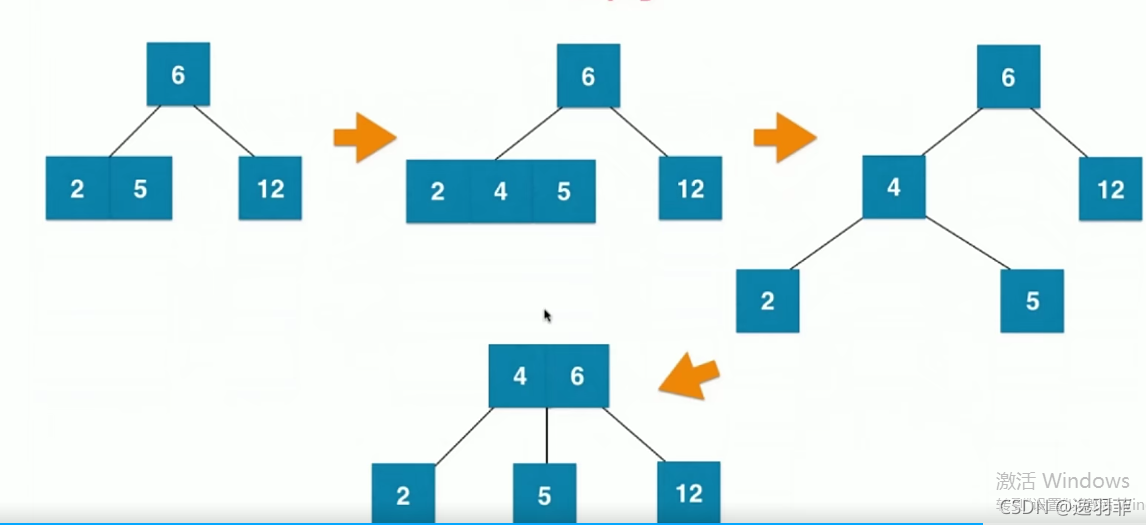
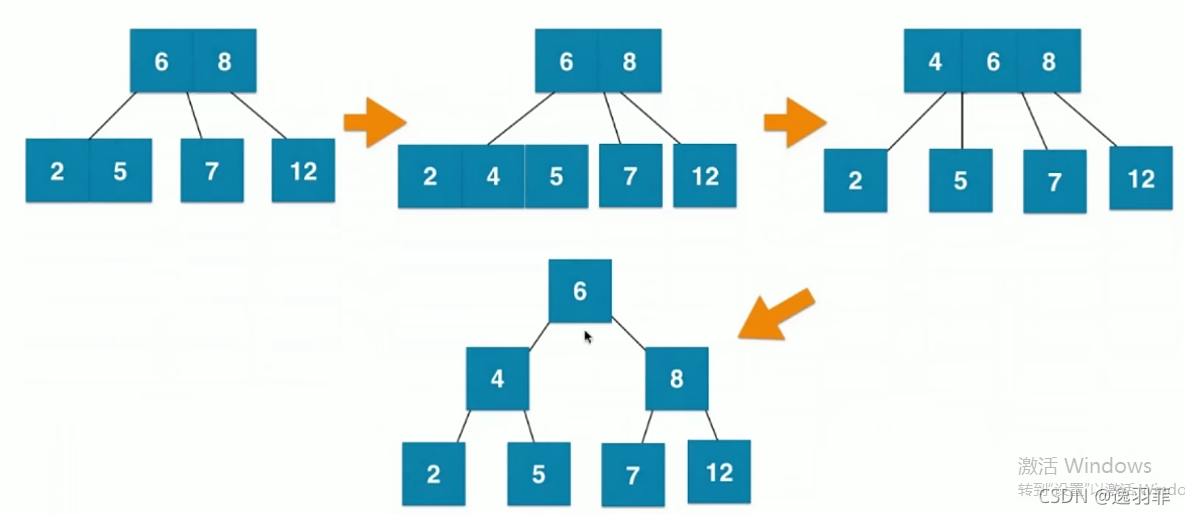
下一篇文章将会写到红黑树。