题目
题意:对于一个数x,有两种操作,
- 减k,数x跳到 x ? k , k ∈ [ 1 , x ? 1 ] x-k,k\in [1,x-1] x?k,k∈[1,x?1]
- 除k, 数x跳到
?
x
/
k
?
,
k
∈
[
2
,
x
]
\lfloor x/k \rfloor, k \in[2,x]
?x/k?,k∈[2,x]
先给定n和m,求从n跳到1有多少种跳法,答案对m取模。
思路:按着官方题解的D1思路来,减法的部分我们可以直接用前缀和维护。对于除法的部分,拆解成两个部分。
对于
k
∈
[
2
,
s
q
r
t
(
n
)
]
k\in[2,sqrt(n)]
k∈[2,sqrt(n)],直接求解加起来
对于
k
∈
[
s
q
r
t
(
n
)
,
n
]
k\in[sqrt(n),n]
k∈[sqrt(n),n],求解每个k对应的
?
x
/
k
?
\lfloor x/k \rfloor
?x/k?落在
[
2
,
s
q
r
t
(
n
)
]
[2,sqrt(n)]
[2,sqrt(n)]的哪个区间(因为k>=sqrt(n),必有
?
x
/
k
?
\lfloor x/k \rfloor
?x/k? <= sqrt(n))。所以这部分的数据,我们可以反过来枚举
?
x
/
k
?
\lfloor x/k \rfloor
?x/k?落在
[
2
,
s
q
r
t
(
n
)
]
[2,sqrt(n)]
[2,sqrt(n)]的数,对应的k的范围。
注意计算的时候对于边界sqrt(n)计算的要注意,不重不漏。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 200010;
int n, mod;
int f[maxn];
/*
* 0 <= a, b < mod
*/
int sub_mod(int a, int b) {
int res = a - b;
if (res < 0) res += mod;
return res;
}
/*
* 0 <= a, b < mod
*/
int add_mod(int a, int b) {
int res = a + b;
if (res >= mod) res -= mod;
return res;
}
int mul(int a, int b) {
return 1LL * a * b % mod;
}
int count(int n, int c) {
int a = n / (c + 1) + 1;
int b = n / c;
return b - a + 1;
}
int main() {
scanf("%d%d", &n, &mod);
f[1] = 1;
int pre = f[1];
for (int i = 2; i <= n; ++i) {
f[i] = pre;
int m = sqrt(1.0 * i);
for (int j = 2; j < m; ++j) {
f[i] = add_mod(f[i], f[i / j]);
}
if (m != i / m && m >= 2) {// 边界sqrt(n)计算的要注意,不重不漏
f[i] = add_mod(f[i], f[i/m]);
}
for (int j = 1; j <= m; ++j) {
f[i] = add_mod(f[i], mul(f[j], count(i, j)));
}
pre = add_mod(pre, f[i]);
}
// for (int i = 1; i <= n; ++i) {
// printf("f[%d]:%d\n", i, f[i]);
// }
printf("%d\n", f[n]);
}
/*
1 2 3 4 5 6
1 2 5 12 25 55
20
{3,4,5}*1
{2}*2
45
{4,5,6}*1
{3}*2
{2}*5
42 998244353
*/
参考这篇博客,写法更简洁,日常觉得大佬的思路比题解的还好。数论分块
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
vector<int> v[maxn];
vector<pair<int,int>> s;
ll dp[maxn];
int main()
{
ll n,m;
cin>>n>>m;
dp[1]=1;
ll sum=1;
for(int i=2;i<=n;i++)
{
dp[i]+=sum;
for(int l=2,r=0;l<=i;l=r+1)
{
// r=min(i,i/(i/l));
r=i/(i/l);
dp[i]+=1ll*dp[i/l]*(r-l+1);
dp[i]%=m;
}
// for(int j=2;j<=i;j++)
// {
// dp[i]+=1ll*dp[i/j];
// dp[i]%=m;
// }
sum+=dp[i];
sum%=m;
}
cout<<dp[n];
return 0;
}
// 作者:爱打CF的小赵同学 https://www.bilibili.com/read/cv12851308 出处:bilibili
对于D2,用了差分的思想。
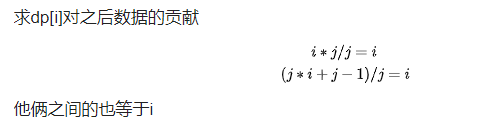
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=6e6+6;
ll dp[maxn];
int main()
{
ll n,m;
cin>>n>>m;
dp[1]=1;
dp[2]=m-1;
for(int i=1;i<=n;i++)
{
dp[i]+=dp[i-1];
dp[i]%=m;
dp[i+1]+=dp[i];
dp[i+1]%=m;
for(ll j=2;j*i<=n;j++)
{
dp[j*i]=dp[j*i]+dp[i];
dp[j*i]%=m;
if(j*i+j<=n)
{
dp[j*i+j]-=dp[i];
dp[j*i+j]%=m;
dp[j*i+j]+=m;
dp[j*i+j]%=m;
}
}
}
cout<<dp[n];
return 0;
}
// 作者:爱打CF的小赵同学 https://www.bilibili.com/read/cv12851308 出处:bilibili