数据结构学习笔记(二叉树)总结与整理
二叉树定义
概念:一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构
二叉树的性质 - 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h- 1.
- 对任何一棵二叉树, 如果度为0其叶结点个数为 n0, 度为2的分支结点个数为 n2,则有n0=n2+1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=Log2(n+1). (ps:Log2(n+1)是log以2为底,n+1为对数)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
二叉树结构
数据结构中的二叉树:

结构定义:
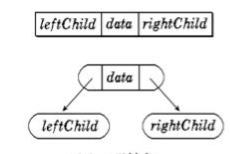
代码表示:
二叉树结构体定义:
// An highlighted block
//结点结构
typedef struct BinTreeNode
{
ElemType data;
struct BinTreeNode *leftChild;
struct BinTreeNode *rightChild;
}BinTreeNode;
//根节点管理
typedef BinTreeNode* BinTree;
void BinTreeInit(BinTree *t);
二叉树常用操作
**初始化**
// An highlighted block
void BinTreeInit(BinTree *t)
{
*t = NULL;
}
二叉树的创建
二叉树创建——**使用指针引用方式**
// An highlighted block
void BinTreeCreate_1(BinTree *t)
{
ElemType item;//接收数据
scanf("%c", &item);
if(item == '#')//判断输入是否为一个结束标记
*t = NULL;//是 说明这棵二叉树是空树
else
{
*t = (BinTreeNode*)malloc(sizeof(BinTreeNode));//创建树(子树)根结点
assert(*t != NULL);
(*t)->data = item;//为结点赋值
BinTreeCreate_1(&(*t)->leftChild);//创建左子树
BinTreeCreate_1(&(*t)->rightChild);//创建右子树
}
}
二叉树创建——**通过返回值返回二叉树**
// An highlighted block
BinTree BinTreeCreate_2()
{
BinTreeNode *t;
ElemType item;//接收数据
scanf("%c", &item);
if(item == '#')//判断输入是否为一个结束标记
return NULL;//返回空
//创建树(子树)根结点
t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t != NULL);
t->data = item;//为结点赋值
t->leftChild = BinTreeCreate_2();//创建左子树
t->rightChild = BinTreeCreate_2();//创建右子树
return t;//返回所创建的树
}
二叉树创建——**使用二级指针**
// An highlighted block
void _BinTreeCreate(BinTreeNode **t)
{
ElemType item;//接收数据
scanf("%c", &item);
if(item == '#')//判断输入是否为一个结束标记
*t = NULL;//是 说明这棵二叉树是空树
else
{
//创建树(子树)根结点
*t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(*t != NULL);
(*t)->data = item;//为结点赋值
_BinTreeCreate(&(*t)->leftChild);//创建左子树
_BinTreeCreate(&(*t)->rightChild);//创建右子树
}
}
**二叉树创建——**传入要创建的二叉树的串进行创建
// An highlighted block
BinTree BinTreeCreate_3(char *str)
{
BinTreeNode *t;
if(*str=='#' || *str=='\0')//判断输入是否为一个结束标记
return NULL;//是 说明这棵二叉树是空树
//创建树(子树)根结点
t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t != NULL);
t->data = *str;//为结点赋值
t->leftChild = BinTreeCreate_3(++str);//创建左子树
t->rightChild = BinTreeCreate_3(++str);//创建右子树
return t;
}
**根据前序遍历和中序遍历来创建二叉树**
// An highlighted block
BinTree BinTreeCreate_VLR_LVR(char *VLR, char *LVR, int n)
{
if(n == 0)
return NULL;
int k = 0;
//利用先序序列,查找根在中序序列的位置
while(VLR[0] != LVR[k])
k++;
//创建根
BinTreeNode *t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t != NULL);
t->data = LVR[k];
t->leftChild = BinTreeCreate_VLR_LVR(VLR+1, LVR, k);//创建t的左子树
t->rightChild = BinTreeCreate_VLR_LVR(VLR+k+1, LVR+k+1, n-k-1);//创建右子树
return t;
}
**根据中序和后序序列创建二叉树**
// An highlighted block
BinTree BinTreeCreate_LVR_LRV(char *LVR, char *LRV, int n)
{
if(n == 0)
t = NULL;
else
{
//利用后序序列,查找根在中序序列的位置
int k = 0;
while(LRV[n-1] != LVR[k]) //后序需要从后往前找根
k++;
//创建根节点
t = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t != NULL);
t->data = LVR[k];
//递归创建右树
BinTreeCreate_LVR_LRV(t->rightChild,LVR+k+1,LRV+k,n-k-1);
//递归创建左树
BinTreeCreate_LVR_LRV(t->leftChild,LVR,LRV,k);
//返回树
return t;
}
递归方式二叉树的遍历
**前序遍历**
// An highlighted block
void BinTreePreOrder(BinTree t)
{
if(t != NULL)//树不为空
{
printf("%c ", t->data); //访问(子树)根结点
BinTreePreOrder(t->leftChild);//访问左子树
BinTreePreOrder(t->rightChild);//访问右子树
}
}
**中序遍历**
// An highlighted block
void BinTreeInOrder(BinTree t)
{
if(t != NULL)//树不为空
{
BinTreeInOrder(t->leftChild);//访问左子树
printf("%c ", t->data); //访问(子树)根结点
BinTreeInOrder(t->rightChild);//访问右子树
}
}
**后序遍历**
// An highlighted block
void BinTreePostOrder(BinTree t)
{
if(t != NULL)
{
BinTreePostOrder(t->leftChild);
BinTreePostOrder(t->rightChild);
printf("%c ", t->data);
}
}
**层次遍历**(需要用到队列结构)
// An highlighted block
void BinTreeLevelOrder(BinTree t)
{
if(t != NULL)
{
LinkQueue Q;//创建队列
LinkQueueInit(&Q);//对队列初始化
LinkQueuePush(&Q, t);//将二叉树根结点(地址)入队
while(!LinkQueueEmpty(&Q))//判断队列是否为空
{
BinTreeNode *node = LinkQueueFront(&Q);//取(子树)根结点(地址)
LinkQueuePop(&Q);//将(子树)根结点(地址)出队
printf("%c ", node->data);//打印出(子树)根结点的数据
if(node->leftChild != NULL)//判断该结点的左树是否为空
LinkQueuePush(&Q, node->leftChild);//否 将左子树(地址)入队
if(node->rightChild != NULL) //判断该结点右子树是否为空
LinkQueuePush(&Q, node->rightChild);//否 将右子树(地址)入队
}
}
}
非递归方式二叉树的遍历
**非递归方式二叉树的前序遍历**(需要用到栈结构)
// An highlighted block
void BinTreePreOrder_NoR(BinTree t)
{
if(t != NULL)//判断二叉树是否为空
{
LinkStack st; //申请一个栈
LinkStackInit(&st);//初始化栈
LinkStackPush(&st, t);//将二叉树的根结点入栈
while(!LinkStackEmpty(&st))//判断栈顶是否为空
{//否
BinTreeNode *p = LinkStackTop(&st);//获取栈顶结点
LinkStackPop(&st);//出栈
printf("%c ", p->data);//打印数据
/*这里需要注意的是栈结构是先进后出的,所以后访问的结点先入栈*/
if(p->rightChild != NULL)//判断右子树是否为空
LinkStackPush(&st, p->rightChild); //否 入栈
if(p->leftChild != NULL)//判断左子树是否为空
LinkStackPush(&st, p->leftChild);//否 入栈
}
}
}
**非递归方式二叉树的中序遍历**(需要用到栈结构)
// An highlighted block
void BinTreeInOrder_NoR(BinTree t)
{
if(t != NULL)//判断二叉树是否为空
{//不空
LinkStack st;//设置一个栈结构
LinkStackInit(&st);//初始化栈
do
{
while(t != NULL)
{
LinkStackPush(&st, t);//将根结点入栈
t = t->leftChild;//位置下移
}
BinTreeNode *p = LinkStackTop(&st);
LinkStackPop(&st);//获取栈顶元素
printf("%c ", p->data);//打印数据
if(p->rightChild != NULL)//判断右子树是否为空
t = p->rightChild;//访问右子树
}
while(!LinkStackEmpty(&st) || t!=NULL);
}
}
**非递归方式二叉树的后序遍历**(需要用到栈结构)
// An highlighted block
void BinTreePostOrder_NoR(BinTree t)
{
if(t != NULL)
{
BinTreeNode *prev = NULL;
LinkStack st;//申请一个栈
LinkStackInit(&st);//初始化
do
{
while(t != NULL)
{
LinkStackPush(&st, t);//入栈
t = t->leftChild;//指向左子树的根结点
}
BinTreeNode *p = LinkStackTop(&st);//获取栈顶元素
if(p->rightChild==NULL || prev==p->rightChild)
{
LinkStackPop(&st);//出栈
printf("%c ", p->data);
prev = p;
}
else
t = p->rightChild;
}while(!LinkStackEmpty(&st));
}
}
二叉树的其他功能
**二叉树的结点个数**
// An highlighted block
size_t Size(BinTree t)
{
if(t == NULL)
return 0;
//左孩子+右孩子节点数+根节点数
return Size(t->leftChild) + Size(t->rightChild) + 1;
}
**二叉树的高度**
// An highlighted block
size_t Height(BinTree t)
{
size_t left_h, right_h;
if(t == NULL)//判断二叉树是否为空,是 记录高度为0
return 0;
//求取左子树高度
left_h = Height(t->leftChild);
right_h = Height(t->rightChild);//求取右子树高度
//返回:该二叉树高度=左子树与右子树的最大高度+1
return (left_h > right_h ? left_h : right_h) + 1;
}
**二叉树叶子节点个数**
// An highlighted block
size_t LeafSize(BinTree t)
{
if(t == NULL)
return 0;
if(t->leftChild==NULL && t->rightChild==NULL)
return 1;
return LeafSize(t->leftChild) + LeafSize(t->rightChild);
}
**二叉树第K层结点个数**
// An highlighted block
size_t LevelKSize(BinTree t, int k)
{
if(t == NULL)
return 0;
if(k == 1)
return 1;
return LevelKSize(t->leftChild, k-1) + LevelKSize(t->rightChild, k-1);
}
**查找二叉树结点**
// An highlighted block
BinTreeNode* Find(BinTree t, ElemType key)
{
BinTreeNode *p;
if(t==NULL || t->data==key)//判断二叉树为空且判断结点值是否等于key值
return t;
//或者可以这么写
//if(t == NULL) //判断二叉树是否为空
//return NULL; //是 说明不存在,返回空
//if(t->data == key) //否 判断结点值是否等于key值
//return t; //是 返回结点地址
p = Find(t->leftChild, key);//查找左子树
if(p != NULL)//判断是否找到
return p;//找到 返回结点地址
// 没找到
return Find(t->rightChild, key);// 查找右子树,返回查找结果
}
**查找某结点的父结点**
// An highlighted block
BinTreeNode* Parent(BinTree t, BinTreeNode *p)
{
BinTreeNode *ret;
if(t==NULL || t->leftChild==p || t->rightChild==p)
return t;
ret = Parent(t->leftChild, p);//查找t的左子树
if(ret != NULL)//判断左子树中是否找到满足条件的结点
return ret;
return Parent(t->rightChild, p);//否,查找右子树
}
**克隆二叉树**
// An highlighted block
BinTreeNode* Clone(BinTree t)
{
BinTreeNode *p;
if(t == NULL)//判断t是否为空
return NULL;//是 则无需拷贝,直接置空
//把t拷贝到p
p = (BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(p != NULL);
p->data = t->data;
p->leftChild = Clone(t->leftChild);//拷贝t左子树到p左子树
p->rightChild = Clone(t->rightChild);//拷贝t右子树到p右子树
return p;
}
**判断两个二叉树是否相等**
// An highlighted block
bool Equal(BinTree t1, BinTree t2)
{
if(t1==NULL && t2==NULL)//t1与t2同为空,则返回true
return true;
if(t1==NULL || t2==NULL)//只要有一个为空,另外一个不为空则返回false
return false;
return ((t1->data==t2->data) && Equal(t1->leftChild, t2->leftChild)
&& Equal(t1->rightChild, t2->rightChild));
}
**摧毁二叉树**
// An highlighted block
void BinTreeDestroy(BinTree *t)
{
if(*t != NULL)//判断二叉树是否为空
{
BinTreeDestroy(&(*t)->leftChild);//清空左子树
BinTreeDestroy(&(*t)->rightChild);//清空右子树
free(*t);//清空(子树)根
*t = NULL;//预防野指针
}
}
堆(二叉树的顺序结构)
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
概念:
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<=K2i+2 ,则称为小堆(或大堆)。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
性质:
1.堆中某个节点的值总是不大于或不小于其父节点的值;
2.堆总是一棵完全二叉树。
结构:

堆的实现
**堆的定义**
// An highlighted block
typedef struct Heap
{
HeapElemType *heap;
size_t capacity;
size_t size;
}Heap;
**堆的初始化**
// An highlighted block
void HeapInit(Heap *php, int sz)
{
php->capacity = sz;
php->heap = (HeapElemType*)malloc(sizeof(HeapElemType) * php->capacity);
assert(php->heap != NULL);
php->size = 0;
}
**堆的创建**
// An highlighted block
void HeapCreate(Heap *php, HeapElemType ar[], int n)
{
php->capacity = n;
php->heap = (HeapElemType*)malloc(sizeof(HeapElemType) * php->capacity);
assert(php->heap != NULL);
for(int i=0; i<n; ++i)
php->heap[i] = ar[i];
php->size = n;
///
//调整堆
int CurPos = (n - 1) / 2; //找到二叉树的最后一个分支
while(CurPos >= 0)
{
_AdjustDown(php, CurPos);//向下调整
CurPos--;
}
}
**堆顶元素**
// An highlighted block
HeapElemType HeapTop(Heap *php)
{
if(HeapIsEmpty(php))
{
printf("堆已空,不能取堆顶元素.\n");
return;
}
return php->heap[0];
}
**堆的插入**(将数据插入到数组最后,再进行向上调整。)
// An highlighted block
void HeapInsert(Heap *php, HeapElemType v)
{
if(HeapIsFull(php))
{
printf("堆空间已满,%d不能插入\n", v);
return;
}
php->heap[php->size] = v;
_AdjustUp(php, php->size);
php->size++;
}
**堆的删除**(删除堆是删除堆顶的数据。将堆顶的数据和最后一个数据交换,然后删除数组最后一个数据,再进行
向下调整算法。)
// An highlighted block
void HeapRemove(Heap *php)
{
if(HeapIsEmpty(php))
{
printf("堆已空,不能删除数据.\n");
return;
}
//删除数据
HeapElemType tmp = php->heap[0];
php->heap[0] = php->heap[php->size-1];
php->heap[php->size-1] = tmp;
php->size--;
//从根开始调整堆
_AdjustDown(php, 0);
}
**堆的展示**
// An highlighted block
void HeapShow(Heap *php)
{
for(int i=0; i<php->size; ++i)
printf("%d ", php->heap[i]);
printf("\n");
}
向下调整算法:
先设定根节点为当前节点(通过下标获取,标记为cur),比较左右子树的值,找出更小的值,用child来标记。比较child和cur的值,如果child比cur小,则不满足小堆的规则,需要进行交换。如果child比cur大,满足小堆的规则,不需要交换,调整结束。处理完一个节点之后,从当前的child出发,循环之前的过程。向下调整(小堆)示例:

**向下调整算法**
// An highlighted block
void _AdjustDown(Heap *php, int start)
{
int i = start;
int j = 2*i + 1;
while(j < php->size)
{
if(j+1<php->size && php->heap[j+1]>php->heap[j])
j++;
if(php->heap[j] > php->heap[i])
{
HeapElemType tmp = php->heap[j];
php->heap[j] = php->heap[i];
php->heap[i] = tmp;
i = j;
j = 2*i + 1;
}
else
break;
}
}
向上调整算法:
先设定倒数的第一个叶子节点为当前节点(通过下标获取,标记为cur),找出他的父亲节点,用parent来标记。比较parent和cur的值,如果cur比parent小,则不满足小堆的规则,需要进行交换。如果cur比parent大,满足小堆的规则,不需要交换,调整结束。处理完一个节点之后,从当前的parent出发,循环之前的过程。

**向上调整算法**
// An highlighted block
void _AdjustUp(Heap *php, int start)
{
int j = start;
int i = (j-1) / 2;
while(j > 0) //说明没有调整到根节点
{
if(php->heap[j] > php->heap[i])
{
//交换数据
HeapElemType tmp = php->heap[j];
php->heap[j] = php->heap[i];
php->heap[i] = tmp;
//向上回溯
j = i;
i = (j-1) / 2;
}
else
break;
}
}
**堆的摧毁**
// An highlighted block
void HeapDestroy(Heap* php)
{
free(php->heap);
php->heap = NULL;
php->capacity = php->size = 0;
}
**判断堆是空还是满的**
// An highlighted block
bool HeapIsFull(Heap *php)
{
return php->size >= php->capacity;
}
bool HeapIsEmpty(Heap *php)
{
return php->size == 0;
}
堆的排序的基本思想:
将待排序序列构造成一个大顶堆此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n-1个元素的次小值。如此反复执行,便能得到一个有序序列了。