[数据结构与算法]堆排序算法

一?基础概念????????????????

? ????????堆的结构可以分为大根堆和小根堆，是一个完全二叉树，而堆排序是根据堆的这种数据结构设计的一种排序，下面先来看看什么是大根堆和小根堆

1.1? 大根堆和小根堆

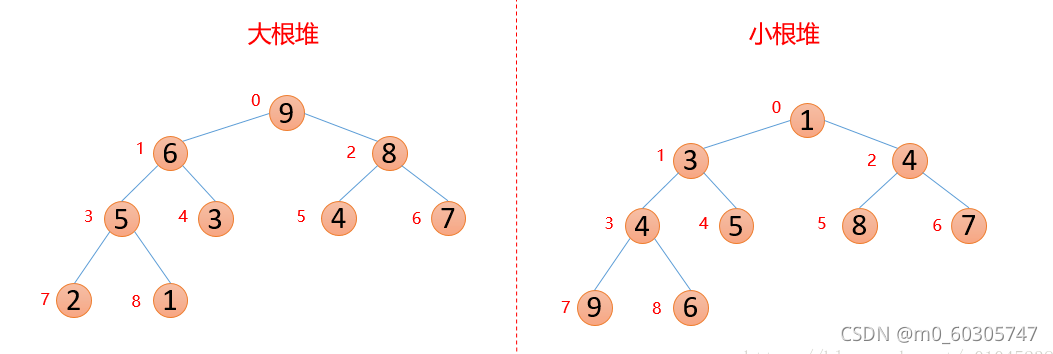
??? ? ? 性质：每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆；每个结点的值都小于其左孩子和右孩子结点的值，称之为小根堆。如下图????????

1.2?条件

父结点索引：(index?- 1) / 2

左孩子索引：2 *?index?+ 1

右孩子索引：2 *?i?+ 2

大根堆：arr(i)>arr(2*i+1) && arr(i)>arr(2*i+2)

小根堆：arr(i)<arr(2*i+1) && arr(i)<arr(2*i+2)

二 堆排序基本步骤

基本思想：

1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

2.1 构造堆

主要思路：每次新插入的数据都与其父结点进行比较，如果插入的数比父结点大，则与父结点交换，否则一直向上交换，直到小于等于父结点，或者来到了顶端。然后固定一个最大值，将剩余的数重新构造成一个大根堆，重复这样的过程。

三?代码

public class test1 {
    public static void main(String[] args) {
        int[] a = { 1,3,4,2,5};
        System.out.println("原始数据：");
        for (int num : a)
            System.out.print(num + " ");
        System.out.println();
        heapSort(a);
        System.out.println("进行堆排序：");
        for (int num : a)
            System.out.print(num + " ");
        System.out.println();


   }

    private static void heapSort(int[] a) {
        if (a == null || a.length <2) {
            return;
        }
        for (int i = 0; i < a.length; i++) {
            heapInsert(a,i); //构造大根堆
        }
        int heapsize = a.length;
//        将0位置的数 与 最后一个数进行交换 并减小heapsize
        swap(a,0 ,--heapsize);
        while (heapsize >0){
//            固定最大值
            heapify(a, 0, heapsize);
            swap(a,0 ,--heapsize);
        }
    }

    private static void heapify(int[] a, int index, int heapsize) {
        int left = index * 2 + 1; //左孩子的下标
        while (left < heapsize) { //存在孩子
//            两个孩子中最大值的下标
            int largest = left + 1 < heapsize && a[left + 1] > a[left] ?
                    left + 1 : left;
//            父亲和孩子谁大 存在largest
            largest = a[largest] > a[index] ? largest : index;
//            如果与父亲的下标就是最大值的下标 则为大根堆，退出循环；
            if (index == largest) {
                break;
            }
            swap(a,largest,index);
            index = largest;
            left = index * 2 + 1;
        }
    }

    private static void heapInsert(int[] a, int index) {
//        判断index位置的值是否大于父节点的值
        while (a[index] > a[(index - 1)/ 2]){
            swap(a,index, (index - 1)/2);
            index = (index - 1)/ 2;
        }
    }

    private static void swap(int[] a, int i, int j) {
        int p = a[i];
        a[i] = a[j];
        a[j] = p;
    }
}