A. Uniform String

题意
给定字符串的长度和使用字符的种类，最大化字符串出现的最小频率。
解题思路
贪心填充即可。
AC代码

/**
  *@filename:A
  *@author: pursuit
  *@csdn:unique_pursuit
  *@email: 2825841950@qq.com
  *@created: 2021-07-28 21:32
**/
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 100000 + 5;
const int P = 1e9+7;

int t,n,k;
void solve(){
    int cnt = 0;
    for(int i = 1; i <= n; ++ i){
        printf("%c", 'a' + (cnt++ % k));
    }
    puts("");
}
int main(){
    scanf("%d", &t);
    while(t -- ){
        scanf("%d%d", &n, &k);
        solve();
    }
    return 0;
}

B. Teams Forming

题意
给定 $n$ 个人的能力值，你需要将他们分成 $n / 2$ 组，每组两人，要求每组的能力值相同。问你需要至少提高多少能力值才可以达成要求。
解题思路
贪心，自然是能力值接近的两个人分在一组，所以我们对能力值进行排序。计算每组的两人的能力值之差总和即可。
AC代码

/**
  *@filename:B
  *@author: pursuit
  *@created: 2021-08-29 14:03
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl

using namespace std;

typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;

int n,a[N];
void solve(){
    sort(a + 1, a + n + 1);
    int ans = 0;
    for(int i = 2; i <= n; i += 2){
        ans += a[i] - a[i - 1];
    }
    printf("%d\n", ans);
}
int main(){	
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i){
        scanf("%d", &a[i]);
    }
    solve();
    return 0;
}

C. Prefixes and Suffixes

题意
有一个字符串 $s$ ，给定其 $2\times n-2$ 的前缀和后缀字符串。要求你输出哪些字符串属于前缀哪些字符串属于后缀。
解题思路
按长度排序，那么易知，长度相同的前缀和后缀相同。同时，如果我们确定了最长的前缀，那么其接下来的长度小的前缀字符串也可以确定；同理，确定了后缀也同样可行。所以我们可以假定哪个是前缀哪个是后缀，再去检测其正确性即可。
AC代码

/**
  *@filename:C
  *@author: pursuit
  *@created: 2021-08-29 14:05
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl

using namespace std;

typedef pair<int,int> pii;
typedef long long ll;
const int N = 200 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;

int n,pos[N];
string s[N];
char ans[N];
bool cmp(int i,int j){
    //按长度排序。
    return s[i].size() > s[j].size();
}
bool check(int x){
    string s1,s2;
    if(x)s1 = s[pos[1]], s2 = s[pos[2]], ans[pos[1]] = 'P', ans[pos[2]] = 'S';
    else s1 = s[pos[2]], s2 = s[pos[1]], ans[pos[1]] = 'S', ans[pos[2]] = 'P';
    int len = n - 2;
    for(int i = 3; i <= 2 * n - 2; i += 2){
        //根据s1和s2判断接下来的是前缀还是后缀。
        int idx1 = pos[i],idx2 = pos[i + 1];
        //debug(n - len);
        if(s1.substr(0,len) == s[idx1] && s2.substr(n - len - 1) == s[idx2]){
            ans[idx1] = 'P', ans[idx2] = 'S';
        }
        else if(s1.substr(0,len) == s[idx2] && s2.substr(n - len - 1) == s[idx1]){
            ans[idx1] = 'S', ans[idx2] = 'P';
        }
        else{
            return false;
        }
        -- len;
    }
    return true;
}
void solve(){
    sort(pos + 1, pos + 2 * n - 1,cmp);
    //间隔的一个是前缀一个是后缀。假定第一个是前缀然后去判断即可。
    if(check(1) || check(0)){
        ans[2 * n - 1] = '\0';
        cout << (ans + 1) << endl;
    }
}
int main(){	
    cin >> n;
    for(int i = 1; i <= 2 * n - 2; ++ i){
        cin >> s[i];
        pos[i] = i;
    }
    solve();
    return 0;
}

D1. Great Vova Wall (Version 1)

题意
有 $n$ 个墙，现在你可以砌砖，砖的大小为 $2\times 1$ 。砖可以放置在等高墙的相邻部分，使得这两个墙的高度都增加 $1$ ，在这个版本中，你还可以垂直放置，使得墙的任何部分的高度都增加 $2$ 。问你是否可以使得墙的所有部分都有相同的高度，且墙里面没有空的空间。
解题思路
对于单个墙来说，我们垂直放置砖块不能改变奇偶性。对于两个相邻的墙且奇偶性相同的，我们可以先垂直放置再水平放置使其相同高。对于所有的墙也一样。所以我们只在乎墙高的奇偶性。然后变成一个奇偶匹配问题即可。即经典的括号匹配问题。
AC代码

/**
  *@filename:D1
  *@author: pursuit
  *@created: 2021-08-29 14:32
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl

using namespace std;

typedef pair<int,int> pii;
typedef long long ll;
const int N = 2e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;

int n,x;

int Stack[N],top,bottom;
void solve(){
    //最后栈顶元素小于等于1即可。因为其他的都已经配对好了可以变成任意高度。
    if(top - bottom <= 1){
        puts("YES");
    }
    else{
        puts("NO");
    }
}
int main(){	
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i){
        scanf("%d", &x);
        x %= 2;
        //如果栈为空或者栈顶元素不能和它匹配。就入栈。
        if(top - bottom == 0 || Stack[top - 1] != x){
            Stack[top ++] = x;
        }
        else{
            -- top;
        }
    }
    solve();
    return 0;
}

D2. Great Vova Wall (Version 2)

题意
和D1不同的一点在于砖块不能垂直放置了。
解题思路
和D1的区别在于我们不能单独对墙进行操作了，即不能单独增加某个墙的高。所以和D1的匹配现在在于是否是相同高度了，当然，如果匹配好了我们仍然是可以将其增高到任意高度。只不过这里需要考虑的就是没有匹配的那个墙是不能增高的，所以我们要判断maxx是否大于等于这个墙的高度。这里特别需要注意的一点就是特判 $2112$ 这种情况，即允许后面的和前面的间隔匹配，只要中间的能匹配上，且中间的值小于左右两边，这是因为中间的匹配好了可以增长到和左右两边高度相同，从而匹配左右两边的。
AC代码

/**
  *@filename:D2
  *@author: pursuit
  *@created: 2021-08-29 14:48
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl

using namespace std;

typedef pair<int,int> pii;
typedef long long ll;
const int N = 2e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;

int n,x,maxx;
int Stack[N],top,bottom;
bool flag = false;
void solve(){
    if(top - bottom > 1 || (top - bottom && Stack[top - 1] < maxx))flag = true;
    printf("%s\n", flag ? "NO" : "YES");
}
int main(){	
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i){
        scanf("%d", &x);
        maxx = max(maxx,x);//更新最大值。
        if(top - bottom){
            if(Stack[top - 1] == x){
                -- top;
            }
            else if(Stack[top - 1] < x){
                //注意这里，只要当前值比x小，说明该值已经无法被挽救回来了。可以自己手动模拟一下。
                flag = true;
                break;
            }
            else{
                Stack[top ++] = x;
            }
        }
        else{
            Stack[top ++] = x;
        }
    }
    solve();
    return 0;
}

E. Minimal Diameter Forest

题意
给你一个森林，其中包含 $n$ 个结点。现在需要你添加边使其成为一颗树，并且树的直径尽可能小。树的直径称为：其任意一对顶点之间最短路径中的最大边数。
解题思路
拼接这些树我们肯定是需要找到每个树的关键点。这里这个关键点不是树的中心，而是该点到其他点的最短路径的最大值最小。然后连接这些树我们也肯定不是以链的方式来串起来，而是通过：

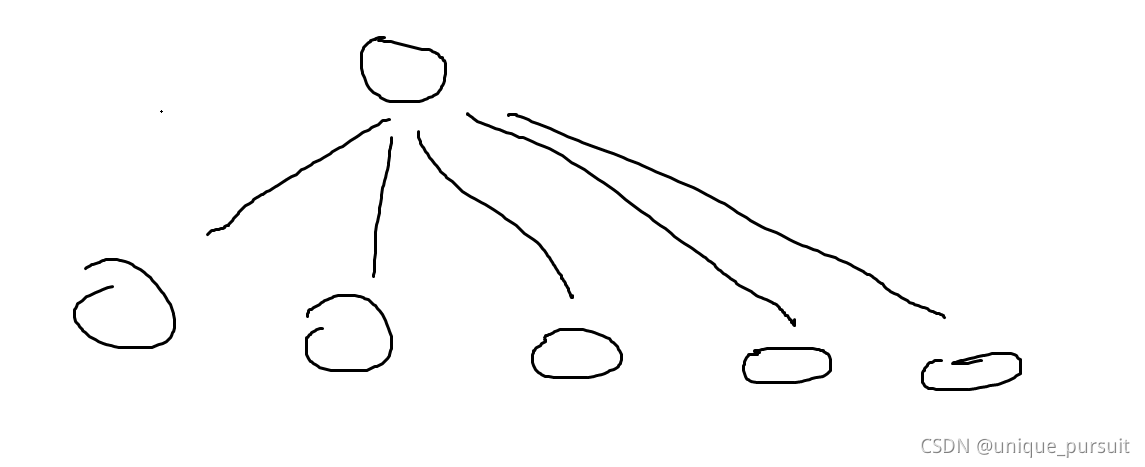
这种方式串起来才是最优的。
经过以上分析，首先，我们需要找到每个树的关键点，这个我们可以先确定每个点所属的连通块。然后根据 $a n s 1$ 数组来确定最小值以及该连通块的关键点，求最短路径我们同样可以通过 $d f s$ 或者 $b f s$ 实现。当然我们也要保存每个连通块的最长路径，因为这也会作为树的直径的参考因素。
考虑完上述，我们考虑拼接点后的直径最长是多少，其中有贡献的则是最长的 $a n s 1 [1]$ 和次长的 $a n s 1 [2]$ 通过 $1$ 这个连通块的关键点连接，所以会多出一条边，即直径为 $a n s 1 [1] + a n s 1 [2] + 1$ ，还有一个则是第二长的 $a n s 1 [2]$ 和 $a n s 1 [3]$ 通过 $1$ 这个连通块的关键点连接，所以会多出来两条边，即直径为 $a n s 1 [2] + a n s 1 [3] + 2$ ，取个max即可。
AC代码

/**
  *@filename:E
  *@author: pursuit
  *@created: 2021-08-29 15:18
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl

using namespace std;

typedef pair<int,int> pii;
typedef long long ll;
const int N = 1e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;

/*
任务是向图中添加一些边，使其成为一棵树且树的直径尽可能小。
找到所有树的重心，再合并在一起即可。
*/
struct edge{
    int to, next;
} edges[N];
int head[N],tot;
int n,m,belong[N],cnt;
int ans1[N],ans2[N],in[N];//ans[i]表示第i个连通块的最小的最大直径。in[i]表示第i个连通块的中心点。
int id[N];
void add(int u,int v){
    edges[++ tot].to = v;
    edges[tot].next = head[u];
    head[u] = tot;
}
bool cmp(int i,int j){
    return ans1[i] > ans1[j];
}
void dfs1(int u){
    belong[u] = cnt;
    for(int i = head[u]; i; i = edges[i].next){
        int v = edges[i].to;
        if(!belong[v])dfs1(v);
    }
}
int dfs2(int u,int fu,int depth){
    int maxx = depth;
    for(int i = head[u]; i; i = edges[i].next){
        int v = edges[i].to;
        if(v == fu)continue;
        maxx = max(maxx,dfs2(v,u,depth + 1));
    }
    return maxx;
}
void solve(){
    //确定每个结点所属的连通分量。
    fill(ans1, ans1 + N, INF);
    for(int i = 1; i <= n; ++ i){
        if(!belong[i]){
            ++ cnt;
            dfs1(i);
        }
    }
    for(int i = 1; i <= n; ++ i){
        int maxx = dfs2(i,-1,0);
        //cout << i << " " << maxx << endl;
        if(maxx < ans1[belong[i]]){
            ans1[belong[i]] = maxx;
            //保存中心点。
            in[belong[i]] = i;
        }
        ans2[belong[i]] = max(ans2[belong[i]], maxx);
    }
    int res = 0;
    for(int i = 1; i <= cnt; ++ i){
        id[i] = i;
        res = max(res,ans2[i]);
    }
    sort(id + 1, id + 1 + cnt,cmp);
    if(cnt >= 2){
        res = max(res, ans1[id[1]] + ans1[id[2]] + 1);
    }
    if(cnt >= 3){
        res = max(res, ans1[id[2]] + ans1[id[3]] + 2);
    }
    printf("%d\n", res);
    for(int i = 2; i <= cnt; ++ i){
        printf("%d %d\n", in[id[1]], in[id[i]]);
    }
}
int main(){	
    scanf("%d%d", &n, &m);
    int u,v;
    for (int i = 1; i <= m; ++ i){
        scanf("%d%d", &u, &v);
        add(u,v), add(v,u);
    }
    solve();
    return 0;
}

F. Tree with Maximum Cost

题意
有一个 $n$ 个结点的无根树，树的每个结点都有一个权值。结点i的权值为 $a_i$ 。
$d i s t (x, y)$ 定义为结点 $x$ 到结点 $y$ 的距离,即结点 $x$ 到结点 $y$ 的简单路径上边的数量。
以结点 $v$ 为根的树的价值定义如下： $\sum_{i=1}^ndist(i,v)·a_i$
请你确定以某个结点为根时树的最大价值。
解题思路
我们可以先通过 $d f s$ 预处理出 $1$ 作为根节点的价值和 $s u m$ 数组， $s u m [u]$ 则表示以 $u$ 为根节点的子树总权值。我们的技巧是通过一开始定的根 $1$ ，然后通过dfs重新生根更新当前的总和。
为什么呢？我们来解释一下。假设原来的根为 $u$ ，现在将根转为 $u$ 的孩子结点 $v$ 。

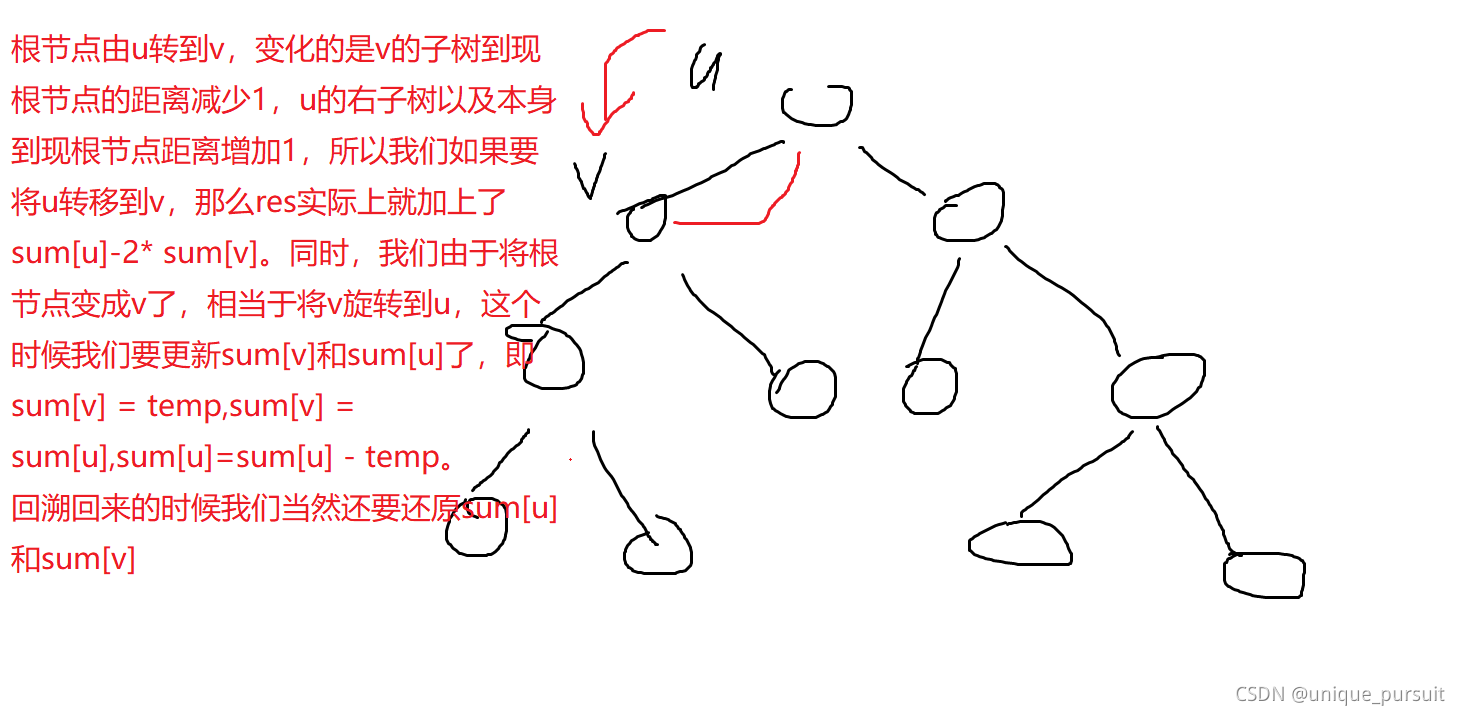
至此，则此题得解。
AC代码

/**
  *@filename:F
  *@author: pursuit
  *@created: 2021-08-29 15:55
**/
#include <bits/stdc++.h>
#define debug(a) cout << "debug : " << (#a)<< " = " << a << endl

using namespace std;

typedef pair<int,int> pii;
typedef long long ll;
const int N = 2e5 + 10;
const int P = 1e9 + 7;
const int INF = 0x3f3f3f3f;

struct edge{
    int to,next;
}edges[N << 1];
int head[N],tot;
int n,a[N];
ll res,sum[N];//sum[u]表示以u为根结点的子树点权和。
void add(int u,int v){
    edges[++ tot].next = head[u];
    edges[tot].to = v;
    head[u] = tot;
}
void dfs1(int u,int fu,int depth){
    res += 1LL * depth * a[u];
    sum[u] = a[u];
    for(int i = head[u]; i; i = edges[i].next){
        int v = edges[i].to;
        if(v == fu)continue;
        dfs1(v,u,depth + 1);
        sum[u] += sum[v];
    }
}
void dfs2(int u,int fu,ll ans){
    res = max(res,ans);
    for(int i = head[u]; i; i = edges[i].next){
        int v = edges[i].to;
        if(v == fu)continue;
        ll temp = ans + sum[u] - 2 * sum[v];
        sum[u] -= sum[v];
        sum[v] += sum[u];
        dfs2(v,u,temp);
        sum[v] -= sum[u];
        sum[u] += sum[v];
    }
}
void solve(){
    dfs1(1,-1,0);
    dfs2(1,-1,res);
    printf("%lld\n", res);
}
int main(){	
    scanf("%d", &n);
    for(int i = 1; i <= n; ++ i){
        scanf("%d", &a[i]);
    }
    int u,v;
    for(int i = 1; i < n; ++ i){
        scanf("%d%d", &u, &v);
        add(u,v), add(v,u);
    }
    solve();
    return 0;
}