[数据结构与算法]数据结构学习笔记（二叉树）OJ题总结与整理

1、单值二叉树

OJ链接：[https://leetcode-cn.com/problems/univalued-binary-tree/]
题目：如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时，才返回 true；否则返回 false。

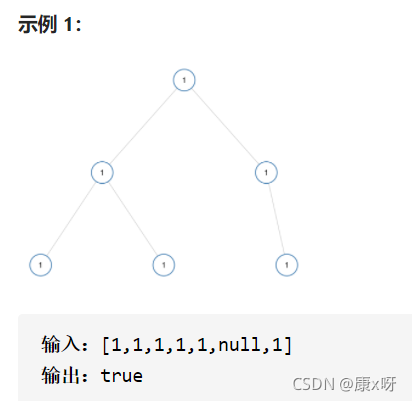
代码：

思路：判断一下结点的值，有不相同的就不是，根节点根左子树右子树的值都是单值进行判断

// An highlighted block
bool isUnivalTree(struct TreeNode* root)
{
    if(root == NULL)
        return true;
        //要么左树是空，要么左树的值等于根节点的值，而且左树还得是单值
    bool left_res = (root->left==NULL || (root->left->val==root->val && isUnivalTree(root->left)));
    //考虑右树
    bool right_res = (root->right==NULL || (root->right->val==root->val && isUnivalTree(root->right)));
    //两者同时都是单值的才是单值二叉树
    return left_res && right_res;
}

2、检查两颗树是否相同

OJ链接：[https://leetcode-cn.com/problems/same-tree/]
题目：给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

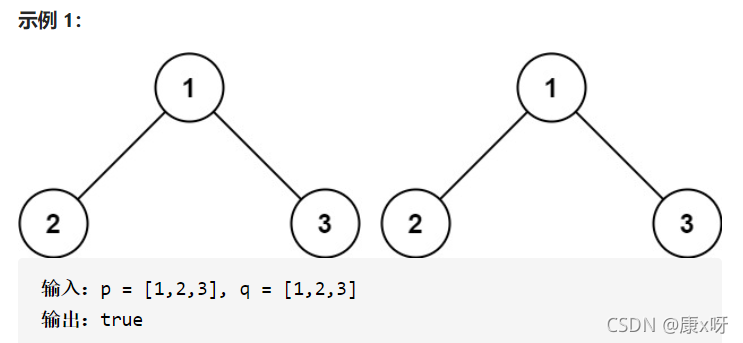
代码：

思路：注意判断p，q都是空的时候

// An highlighted block
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(p==NULL && q==NULL)//p，q都是空的，那么相等
        return true;
    if(p==NULL || q==NULL)//两个有一个不是空，那么不成立
        return false;
    //p，q的值相等并p的左树和q的左树相等，并上p的右树和q的右树相等。
    return p->val==q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

3、对称二叉树

OJ链接：[https://leetcode-cn.com/problems/symmetric-tree/]
题目：给定一个二叉树，检查它是否是镜像对称的。
例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

代码：

思路：利用递归的方式，自己先写一个函数实现，实现方式于上题类似。

// An highlighted block
bool _isSymmetric(struct TreeNode* t1, struct TreeNode* t2)
//判断t1和t2是否对称
{
    if(t1==NULL && t2==NULL)
        return true;
    if(t1==NULL || t2==NULL)
        return false;
        //左右树都存在，t1值和t2的值是否相等的前提下，t1的左树和t2的右树判断相等不，同样判断t1右树和t2左树进行判断
    return (t1->val==t2->val && _isSymmetric(t1->left, t2->right) && _isSymmetric(t1->right, t2->left));
}

bool isSymmetric(struct TreeNode* root)
{
    if(root == NULL)
        return true;
    return _isSymmetric(root->left, root->right);
}

4、二叉树的前序遍历

OJ链接：[https://leetcode-cn.com/problems/binary-tree-preorder-traversal/]
题目：给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

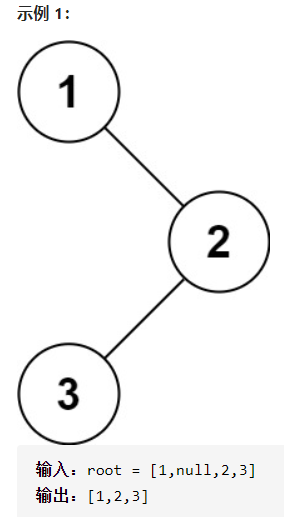
代码：

思路：先求节点长度，然后开辟数组空间，编写内部方法进行递归遍历。

// An highlighted block
size_t Size(struct TreeNode *root)//求长度的函数
{
    if(root == NULL)
        return 0;
    return Size(root->left) + Size(root->right) + 1;
}
//遍历的方法——根—>左—>右
void _preorderTraversal(struct TreeNode*root, int *preorder_array, int *i)
{
    if(root != NULL)
    {
        preorder_array[*i] = root->val;//数据放到root所指的val
        (*i)++;//修改外面的下标
        _preorderTraversal(root->left, preorder_array, i);//遍历左树
        _preorderTraversal(root->right, preorder_array, i);//遍历右树
    }    
}

int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    int n = Size(root);//结点个数
    int *preorder_array = (int*)malloc(sizeof(int) * n);//开辟数组空间
    *returnSize = n;//n个结点

    int index = 0;//下标从0开始
    //给出一个内部方法去递归遍历
    _preorderTraversal(root, preorder_array, &index);//把树放进去，把前序遍历的空间放进去，再把下标地址放进去。最后返回的是遍历之后的结果
    return preorder_array;
}

5、二叉树中序遍历

OJ链接：[https://leetcode-cn.com/problems/binary-tree-inorder-traversal/]
题目：给定一个二叉树的根节点 root ，返回它的中序遍历。

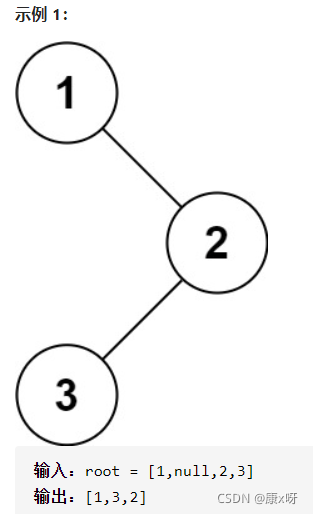
代码：

思路：与上题一致，只需变换遍历的顺序

// An highlighted block
size_t Size(struct TreeNode *root)//求长度
{
    if(root == NULL)
        return 0;
    return Size(root->left) + Size(root->right) + 1;
}
//遍历的方法——左—>根—>右
void _inorderTraversal(struct TreeNode*root, int *inorder_array, int *i)
{
    if(root != NULL)
    {
        _inorderTraversal(root->left, inorder_array, i);
        inorder_array[*i] = root->val;
        (*i)++;
        _inorderTraversal(root->right, inorder_array, i);
    }    
}

int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
    int n = Size(root);
    int *inorder_array = (int*)malloc(sizeof(int) * n);
    *returnSize = n;

    int index = 0;
    _inorderTraversal(root, inorder_array, &index);
    return inorder_array;
}

6、二叉树的后序遍历

OJ链接： [https://leetcode-cn.com/problems/binary-tree-postorder-traversal/]
题目：给定一个二叉树，返回它的后序遍历。

代码：

思路：与上题一致，只需变换遍历的顺序

// An highlighted block
int size(struct TreeNode *t)
{
    if(t == NULL)
        return 0;
    else
        return size(t->left) + size(t->right) + 1;
}

void _postorderTraversal(struct TreeNode *root, int *postorder_array, int *i)
{
    if(root != NULL)
    {
        _postorderTraversal(root->left, postorder_array, i);
        _postorderTraversal(root->right, postorder_array, i);
                 
        postorder_array[*i] = root->val;
        (*i)++;
    }
}

int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
    int n = size(root);
    int *postorder_array = (int*)malloc(sizeof(int) * n);
    *returnSize = n;

    int index = 0;
    _postorderTraversal(root, postorder_array, &index);
    return postorder_array;
}

7、另一颗树的子树

OJ链接：[https://leetcode-cn.com/problems/subtree-of-another-tree/]
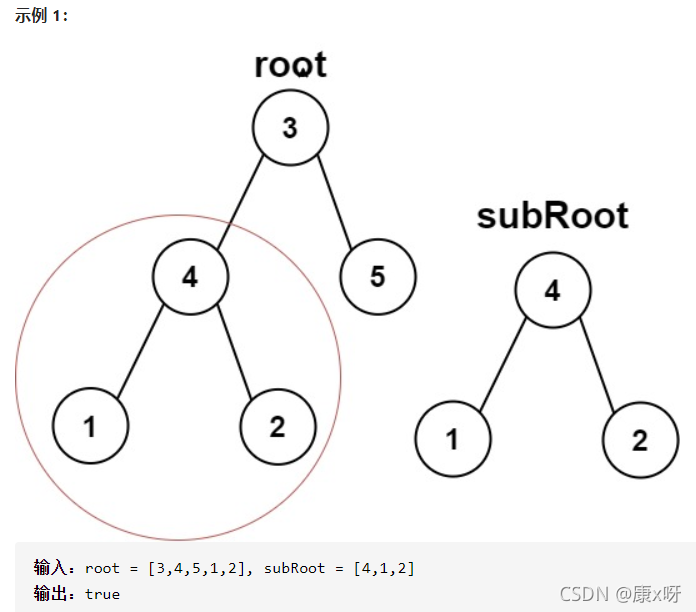
题目：给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

代码：

思路：注意（二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点），进行内部递归调用。

// An highlighted block
//判断这两个树是不是互为子树
bool _isSubtree(struct TreeNode *root, struct TreeNode *subRoot)
{
    if(root==NULL && subRoot==NULL)
        return true;
    if(root==NULL || subRoot==NULL)
        return false;
    //根的值根subRoot相等并上根的左树和子树的左树相等并上子树的右树和子树的右树相等
    return root->val==subRoot->val && _isSubtree(root->left, subRoot->left) && _isSubtree(root->right, subRoot->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(subRoot == NULL)//空树是一切树的子树
        return true;
    if(root == NULL)
        return false;
    if(_isSubtree(root, subRoot))
        return true;
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}