优先级队列及高频考点TopK问题
堆
堆本质上是一个二叉树,满足以下几个条件:
1.完全二叉树。
2.对于树中的任意节点,满足根节点小于左右子树的值(小堆),满足根节点大于左右子树的值(大堆),一个堆如果是小堆,就不可能是大堆。
堆的用处:
堆最大的用处就是能让我们快速找到一个树中的最大值或者最小值(根节点)。
向下调整与向上调整
调整原因:一旦堆中元素发生改变(插入/删除)都需要调整堆的结构,让堆的规则不被破环
过程:下面以小堆来介绍向下调整
1.先设定根节点为当前节点
2.找到当前节点的左右子树的值(通过下标获取,左子树下标=当前节点下标*2+1,右子树下标=当前节点下标 *2+2)
3.比较左右子树的值,找出谁更小,用child进行标记。
4.如果child比parent小,不符合小堆规则,进行交换
5.如果child比parent大,符合小堆规则,不需要交换,整个调整结束
6.处理完一个节点后,从child出发,循环刚才的过程。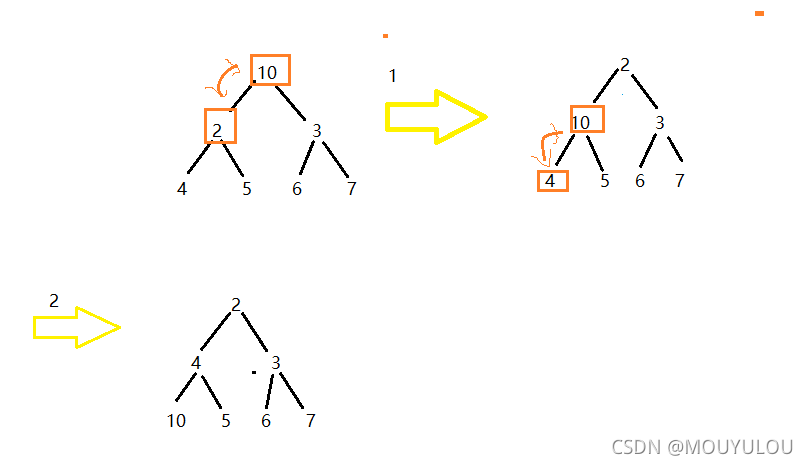
代码实现:
//通过size指定array中那些元素是有效的堆元素
//index表示从哪个位置的下标开始调整
public static void shiftDown(int[] array,int size,int index) {
int parent=index;
int child=parent*2+1;//根据parent下标找当左子树下标
while (child<size) {
//比较左右子树找到较小值
if(child+1<size&&array[child+1]<array[child]) {
child++;
}
//当child位置元素与parent位置元素时进行比较
if(array[child]<array[parent]) {
//不符合小堆规则,交换节点
int tmp=array[child];
array[child]=array[parent];
array[parent]=tmp;
} else {
//调整完毕,不需要继续
break;
}
//更新parent和child
parent=child;
child=parent*2+1;
}
}
调整的作用:借助向下调整,就可以把一个数组构建成堆
从倒数第一个非叶子节点开始,从后往前遍历数组,针对每个位置,依次向下调整即可。
建堆代码:
public static void createHeap(int[] array,int size) {
for (int i = (size-1-1)/2; i >=0 ; i--) {
//size-1得的最后一个叶子节点再-1/2就得到了最后一个节点的父节点(也就是倒数第一个非叶子节点)
shiftDown(array,size,i);
}
}
堆的应用-优先级队列
在很多应用中,我们通常需要按照优先级情况对待处理对象进行处理,比如首先处理优先级最高的对象,然后处理次高的对象。最简单的一个例子就是,在手机上玩游戏的时候,如果有来电,那么系统应该优先处理打进来的电话。
在这种情况下,我们的数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这
种数据结构就是优先级队列(Priority Queue)。
入队列,出队列,返回队首元素
以下都以大堆为例
入队列
- 首先按尾插方式放入数组
- 比较其和其双亲的值的大小,如果双亲的值大,则满足堆的性质,插入结束
- 否则,交换其和双亲位置的值,重新进行 2、3 步骤
- 直到根结点
private int[] array=new int[100];
private int size=0;
public void offer(int x) {
array[size]=x;
size++;
//把新加入元素进行向上调整
shiftUp(array,size-1);
}
public static void shiftUp(int[] array,int index) {
int child=index;
int parent=(index-1)/2;
while (child>0) {
if(array[child]>array[parent]) {
//当前不符合大堆要求
int tmp=array[child];
array[child]=array[parent];
array[parent]=tmp;
} else {
//父节点比子节点大符合要求
break;
}
child=parent;
parent=(child-1)/2;
}
}
出队列
1.要想删除堆顶元素,直接把数组中最后一个元素赋值到堆顶元素上,同时size–就把最后一个元素删除了。
2.接下来从根节点出发进行向下调整。
public int poll() {
//下标为0的元素是对手元素,删掉的同时,也希望剩下的结构仍然是一个堆
int oldValue=array[0];
array[0]=array[size-1];
size--;
shiftDown(array,size,0);
return oldValue;
}
public static void shiftDown(int[] array,int size,int index) {
int parent=index;
int child=parent*2+1;//根据parent下标找当左子树下标
while (child<size) {
//比较左右子树找到较小值
if(child+1<size&&array[child+1]<array[child]) {
child++;
}
//当child位置元素与parent位置元素时进行比较
if(array[child]<array[parent]) {
//不符合小堆规则,交换节点
int tmp=array[child];
array[child]=array[parent];
array[parent]=tmp;
} else {
//调整完毕,不需要继续
break;
}
//更新parent和child
parent=child;
child=parent*2+1;
}
}
返回队首元素
返回堆顶元素
public int peek() {
return array[0];
}
TopK问题
常见问题:给定100亿个数字,让你找出前1000大的数字
两种不同的解决方案:
1.用一个数组保存刚才的那些数字,直接在这个数组上建大堆,循环1000次进行取堆顶元素+调整操作,就可以得到前1000大元素。(内存可能放不下)
2.先取集合中的前1000个元素放到一个数组中,建立一个小堆,一个一个遍历集合中的数字,依次和堆顶元素进行比较,如果这个元素比堆顶元素大,就把堆顶元素删除(调整堆),再把当前元素入堆(调整堆)。当把所有的元素都遍历完之后,堆中的元素就是前1000大的元素.
下面以leetcode中.查找和最小的K对数字为例讲解。
1.把所有的数对都获取到。
2.把数对放到优先队列中。
3.再从优先队列中取前K对数对即可。
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
//创建了一个大堆 比较o2-o1
PriorityQueue<List<Integer>> priorityQueue=new PriorityQueue<>(k, new Comparator<List<Integer>>() {
@Override
public int compare(List<Integer> o1, List<Integer> o2) {
return (o2.get(0)+o2.get(1))-(o1.get(0)+o1.get(1));
}
});
for (int i = 0; i <nums1.length ; i++) {
for (int j = 0; j <nums2.length ; j++) {
if(priorityQueue.size()<k) {
List<Integer> ret=new ArrayList<>();
ret.add(nums1[i]);
ret.add(nums2[j]);
priorityQueue.offer(ret);
} else {
List<Integer> tmp=priorityQueue.peek();
if((tmp.get(0)+tmp.get(1))>(nums1[i]+nums2[j])) {
priorityQueue.poll();
List<Integer> ret=new ArrayList<>();
ret.add(nums1[i]);
ret.add(nums2[j]);
priorityQueue.offer(ret);
}
}
}
}
List<List<Integer>> ret=new ArrayList<>();
for (int i = 0; i <k&&!priorityQueue.isEmpty() ; i++) {
ret.add(priorityQueue.poll());
}
return ret;
}