往期内容在这里:
大家好,继续为大家推荐200道大数据面试常考Leetcode算法题,这期为--动态规划再进阶(序列类动态规划问题)篇,附带解析,都是从Leetcode官网总结大神们的解法(在这里感谢大神的帮助,我只是个搬运工!)这篇更新3篇,艾瑞巴迪和我一起刷起来!!
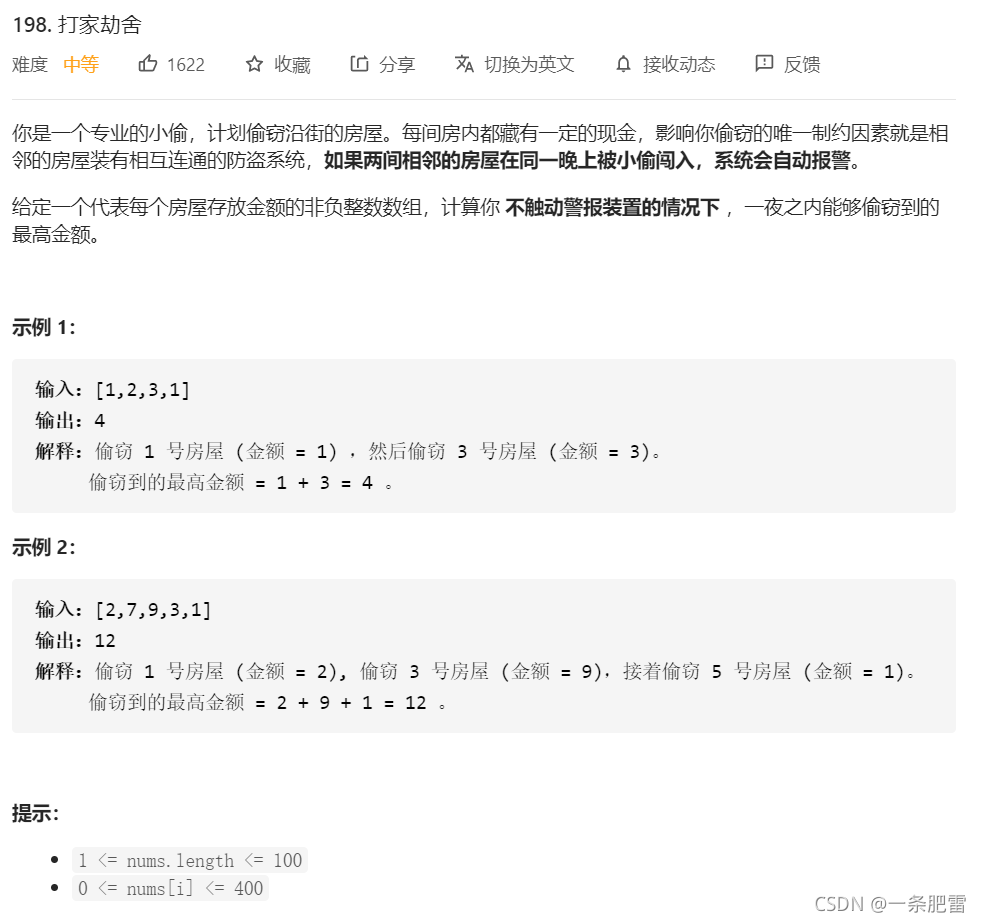
200道大数据面试常考Leetcode算法题(动态规划再进阶(序列类动态规划问题)篇)198-打家劫舍
Leetcode原题:
题解为:
class Solution(object): def rob(self, nums): # 容错处理 if not nums: return 0 if len(nums) < 2: return nums[-1] lenNums = len(nums) # 定义返回结果数组 dp = [0 for _ in range(lenNums)] # 假如只有一间那么就只偷一间 dp[0] = nums[0] # 假如有第二间看第一间钱多还是第二间钱多 dp[1] = nums[0] if nums[0] > nums[1] else nums[1] #从第三间开始判断第一间加上第三间是否大于第二间 for i in range(2, lenNums): dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]) # 返回最后一个数 return dp[lenNums - 1]
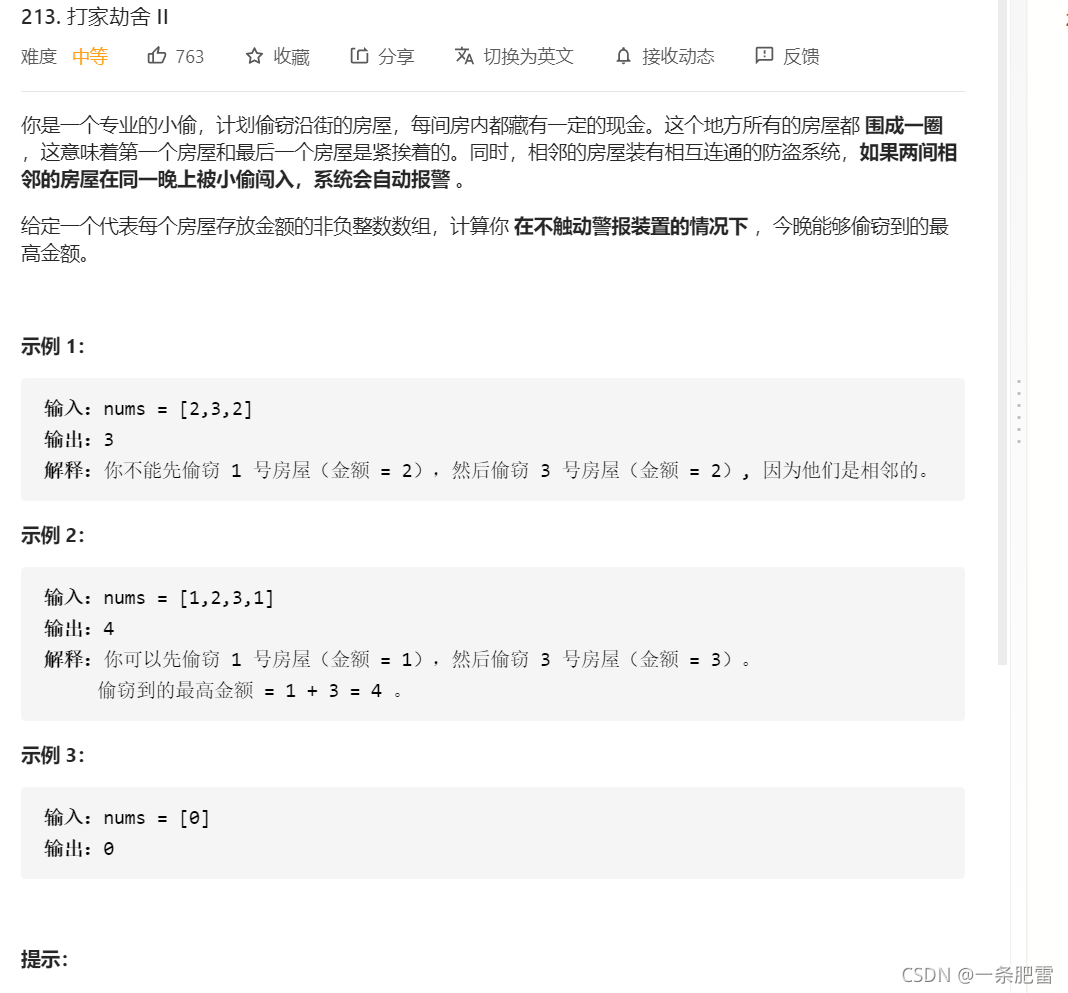
200道大数据面试常考Leetcode算法题(动态规划再进阶(序列类动态规划问题)篇)213-打家劫舍II
Leetcode原题:
题解为:?
class Solution: def robII(self, nums): # 容错处理 if not nums: return 0 if len(nums) < 2: return nums[-1] lenNums = len(nums) # 定义返回结果数组 dp = [0 for _ in range(lenNums)] # 假如只有一间那么就只偷一间 dp[0] = nums[0] # 假如有第二间看第一间钱多还是第二间钱多 dp[1] = nums[0] if nums[0] > nums[1] else nums[1] #从第三间开始判断第一间加上第三间是否大于第二间 for i in range(2, lenNums): dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]) # 返回最后一个数 return dp[lenNums - 1] def rob(self,nums): lenNums = len(nums) if not nums: return 0 if lenNums == 1: return nums[0] # 截取除开第一个跟最后一个剩下的数组分别带进去即可 return max(self.robII(nums[0:lenNums-1]),self.robII(nums[1:lenNums]))
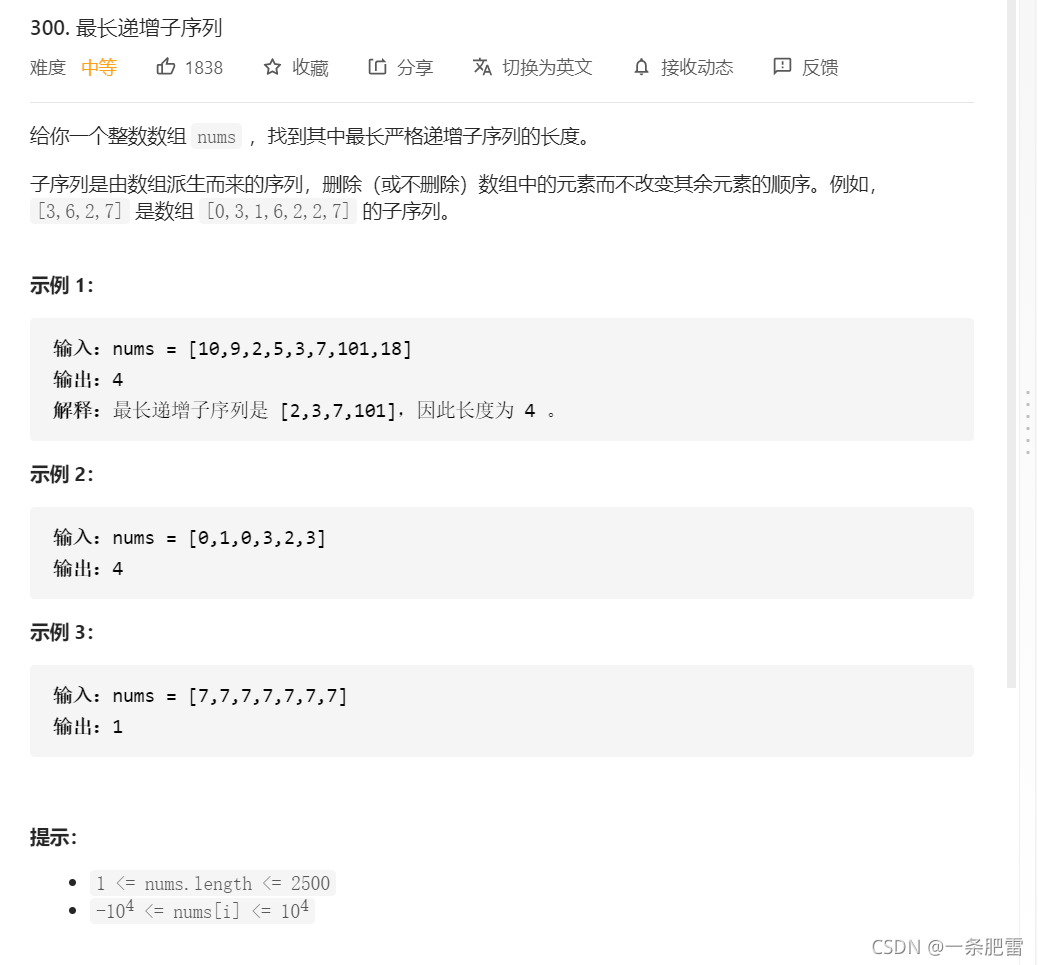
200道大数据面试常考Leetcode算法题(动态规划再进阶(序列类动态规划问题)篇)300-最长递增子序列
Leetcode原题:
?题解为:
class Solution: def lengthOfLIS(self, nums: List[int]) -> int: # 容错判断 if not nums: return 0 # 初始化状态数组 dp = [1] * len(nums) # 对数组循环 for i in range(len(nums)): # 对当前数之前的所有数进行遍历判断 for j in range(i): # 判断之前数是否小于当前数 if nums[j] < nums[i]: # 如果要求非严格递增,将此行 '<' 改为 '<=' 即可。 # dp[i] 以 nums[i] 结尾 的「上升子序列」的长度 # dp[j]+1 为当前最大子序列长度 dp[i] = max(dp[i], dp[j] + 1) # 状态数组 dp 的最大值 return max(dp)