符号表
定义:
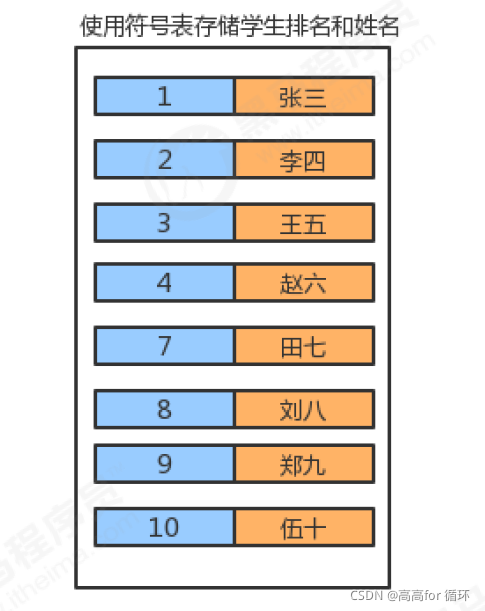
- 符号表最主要的目的就是将一个键和一个值联系起来,符号表能够将存储的数据元素是一个键和一个值共同组成的键值对数据,我们可以根据键来查找对应的值。
符号表中,键具有唯一性。
使用场景:
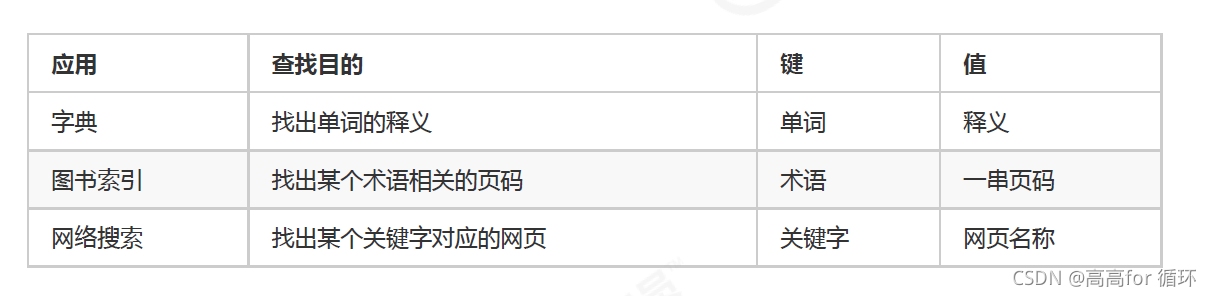
符号表在实际生活中的使用场景是非常广泛的,见下表:
链表实现
符号表API设计:
结点类:

符号表:

代码实现:
public class SymbolTable<Key,Value> {
//记录首结点
private Node head;
//记录符号表中元素的个数
private int N;
public SymbolTable() {
this.head = new Node(null,null,null);
this.N=0;
}
//获取符号表中键值对的个数
public int size(){
return N;
}
//往符号表中插入键值对
public void put(Key key,Value value){
//符号表中已经存在了键为key的键值对,那么只需要找到该结点,替换值为value即可
Node n = head;
while(n.next!=null){
//变换n
n = n.next;
//判断n结点存储的键是否为key,如果是,则替换n结点的值
if (n.key.equals(key)){
n.value = value;
return;
}
}
//如果符号表中不存在键为key的键值对,只需要创建新的结点,保存要插入的键值对,把新结点插入到链表的头部 head.next=新结点即可
Node newNode = new Node(key, value, null);
Node oldFirst = head.next;
newNode.next = oldFirst;
head.next = newNode;
//元素个数+1;
N++;
}
//删除符号表中键为key的键值对
public void delete(Key key){
//找到键为key的结点,把该结点从链表中删除
Node n = head;
while(n.next!=null){
//判断n结点的下一个结点的键是否为key,如果是,就删除该结点
if (n.next.key.equals(key)){
n.next = n.next.next;
N--;
return;
}
//变换n
n = n.next;
}
}
//从符号表中获取key对应的值
public Value get(Key key){
//找到键为key的结点
Node n = head;
while(n.next!=null){
//变换n
n = n.next;
if (n.key.equals(key)){
return n.value;
}
}
return null;
}
//节点类
private class Node{
//键
public Key key;
//值
public Value value;
//下一个结点
public Node next;
public Node(Key key, Value value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
}
测试:
public class SymbolTableTest {
public static void main(String[] args) {
//创建符号表对象
SymbolTable<Integer, String> symbolTable = new SymbolTable<>();
//测试put方法(插入,替换)
symbolTable.put(1,"乔峰");
symbolTable.put(2,"虚竹");
symbolTable.put(3,"段誉");
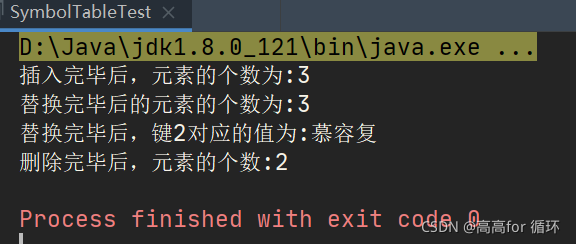
System.out.println("插入完毕后,元素的个数为:"+symbolTable.size());
symbolTable.put(2, "慕容复");
System.out.println("替换完毕后的元素的个数为:"+symbolTable.size());
//测试get方法
System.out.println("替换完毕后,键2对应的值为:"+symbolTable.get(2));
//测试删除方法
symbolTable.delete(2);
System.out.println("删除完毕后,元素的个数:"+symbolTable.size());
}
}
有序符号表
- 刚才实现的符号表,我们可以称之为无序符号表,因为在插入的时候,并没有考虑键值对的顺序,而在实际生活中,有时候我们需要根据键的大小进行排序,插入数据时要考虑顺序,那么接下来我们就实现一下有序符号表。
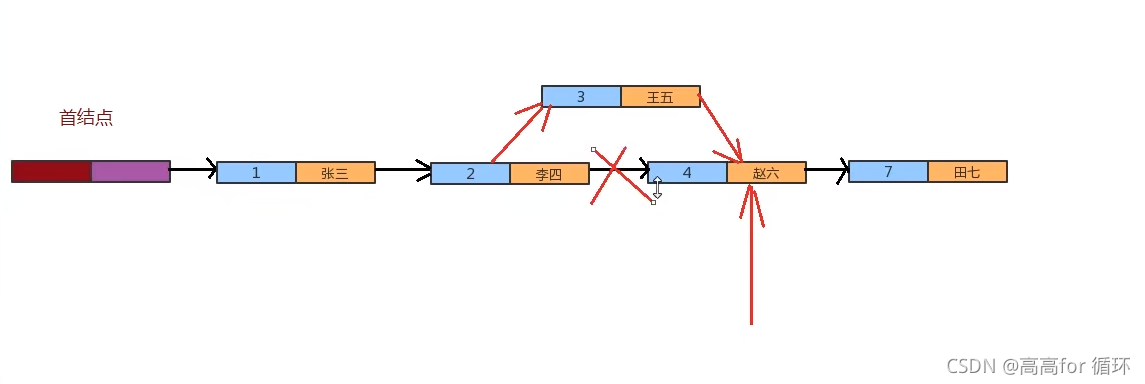
有序链表实现:
public class OrderSymbolTable<Key extends Comparable<Key>,Value> {
//记录首结点
private Node head;
//记录符号表中元素的个数
private int N;
private class Node{
//键
public Key key;
//值
public Value value;
//下一个结点
public Node next;
public Node(Key key, Value value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
}
public OrderSymbolTable() {
this.head = new Node(null,null,null);
this.N=0;
}
//获取符号表中键值对的个数
public int size(){
return N;
}
//往符号表中插入键值对
public void put(Key key,Value value){
//定义两个Node变量,分别记录当前结点和当前结点的上一个结点
Node curr = head.next;
Node pre = head;
while(curr!=null && key.compareTo(curr.key)>0){
//变换当前结点和前一个结点即可
pre = curr;
curr = curr.next;
}
//如果当前结点curr的键和要插入的key一样,则替换
if (curr!=null && key.compareTo(curr.key)==0){
curr.value = value;
return;
}
//如果当前结点curr的键和要插入的key不一样,把新的结点插入到curr之前
Node newNode = new Node(key, value, curr);
pre.next = newNode;
//元素的个数+1;
N++;
}
//删除符号表中键为key的键值对
public void delete(Key key){
//找到键为key的结点,把该结点从链表中删除
Node n = head;
while(n.next!=null){
//判断n结点的下一个结点的键是否为key,如果是,就删除该结点
if (n.next.key.equals(key)){
n.next = n.next.next;
N--;
return;
}
//变换n
n = n.next;
}
}
//从符号表中获取key对应的值
public Value get(Key key){
//找到键为key的结点
Node n = head;
while(n.next!=null){
//变换n
n = n.next;
if (n.key.equals(key)){
return n.value;
}
}
return null;
}
}
debug测试:
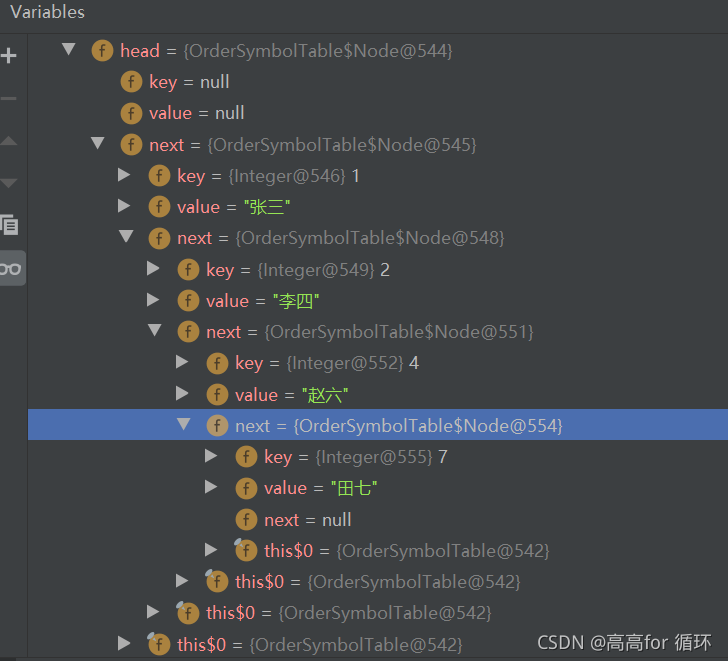
数组二分查找实现:
使用一对平行数组,一个存储键一个存储值。
- 二分查找的思想是在内部维护一个按照key排好序的二维数组,每一次查找的时候,跟中间元素进行比较,如果该元素小,则继续左半部分递归查找,否则继续右半部分递归查找。整个实现代码如下:
- 二分查找的 rank() 方法至关重要,当键在表中时,它能够知道该键的位置;当键不在表中时,它也能知道在何处插入新键。
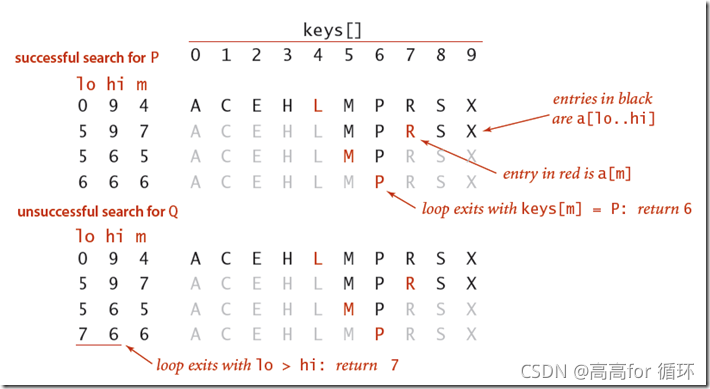
/**
* 有序数组符号表
*/
public class SymbolTable<K extends Comparable<K>,V> {
private K[] keys;//键数组
private V[] values;//值数组
public int size;
private static final int initSize = 10; //默认数组初始大小
public SymbolTable(){
this(initSize);
}
public SymbolTable(int capacity) {
keys = (K[]) new Comparable[capacity];
values = (V[]) new Object[capacity];
}
/**
* 查找键为K的值
*/
public V get(K k){
if(isEmpty()){
return null;
}
//在数组中找出值
int i = rank(k);
if(i < size && keys[i].compareTo(k) == 0){
return values[i];
}
return null;
}
/**
* 插入要给键值对
*/
public void put(K k,V v){
int i = rank(k);
//如果已经存在了键,就交换值
if(i < size && keys[i].compareTo(k)==0){
values[i] = v;
return;
}
//否则就把键值插入到最小于K的值之后
for(int j = size ;j>i ; j--){
keys[j] = keys[j - 1];
values[j] = values[j - 1];
}
keys[i] = k;
values[i] = v;
size ++;
}
public boolean isEmpty(){
return size == 0;
}
public int rank(K k){
int low = 0;//低位起始下标
int high = size-1;//高位下标,长度-1
//高低交叉之前都一直查询
while(low <= high){
int mid = low + (high - low) /2;//找到中位下标
int cmd = k.compareTo(keys[mid]);//获取数组中中位值与比较K的大小
//如果两个值相等,说明找到了
if(cmd == 0){
return mid;
//小于0说明比中位值小,从数组中中位置左侧搜索
}else if(cmd < 0){
high = mid - 1;
//和上面相反,从数组右侧搜索
}else {
low = mid + 1;
}
}
//否侧返回低位的值,这个值就是小于被查找值的数量
return low;
}
}
debug测试:
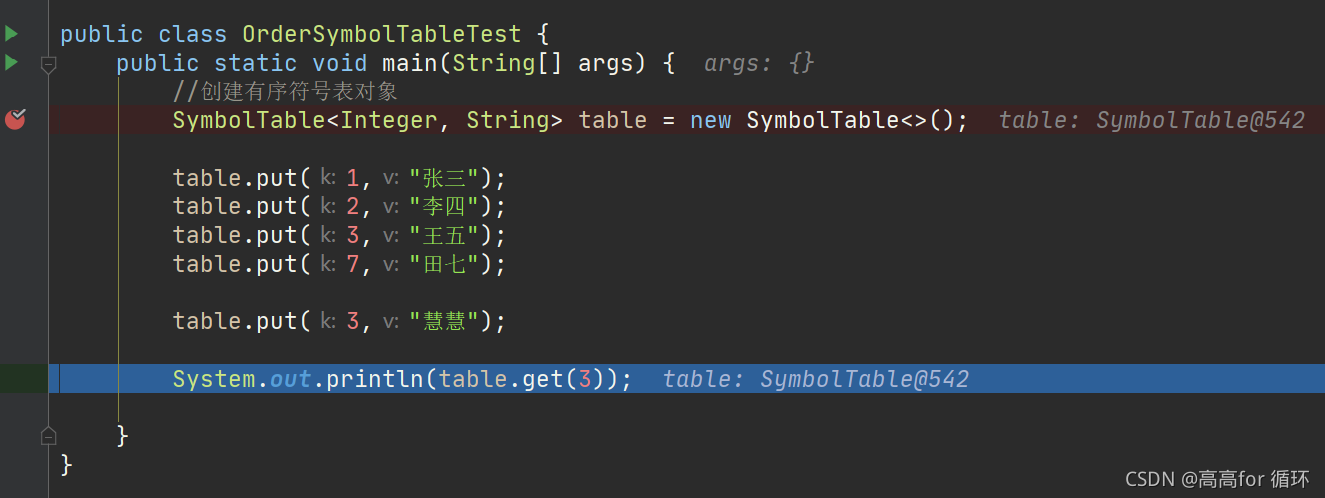
总结:
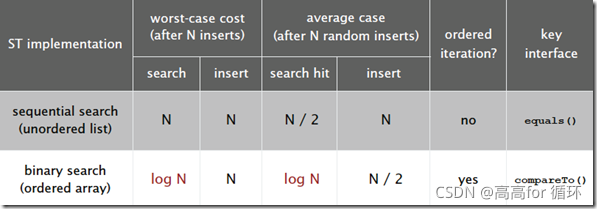
本文介绍了符号表这一抽象数据结构,然后介绍了两种基本实现:基于无序链表的实现和基于有序数组的实现,两种实现的时间复杂度如下:
无序链表实现:
- 插入的时候先要查找,如果存在则更新value,查找的时候需要从链表头进行查找,所以插入和查找的平均时间复杂度均为O(n)
数组二分查找:
- 采用二分查找只需要最多 logN+1次的比较即可找到对应元素,所以查找效率比较高。
- 但是对于插入元素来说,每一次插入不存在的元素,需要将该元素放到指定的位置,然后,将他后面的元素依次后移,所以平均时间复杂度O(n),对于插入来说效率仍然比较低。
使用有序数组的二分查找法提高了符号表的查找速度,但是插入效率仍旧没有得到提高,而且在要维护数组有序,还需要进行排序操作。这两种实现方式简单直观,但是无法同时达到较高查找和插入效率。
本文只是一个引子,后面的系列文章将会介绍二叉查找树,平衡查找树以及哈希表。