[数据结构与算法]动态规划算法

概念引入

在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定，它依赖于当前面临的状态，又影响以后的发展。当各个阶段决策确定后，就组成一个决策序列，因而也就确定了整个过程的一条活动路线．这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程，这种问题称为多阶段决策问题。在多阶段决策问题中，各个阶段采取的决策，一般来说是与时间有关的，决策依赖于当前状态，又随即引起状态的转移，一个决策序列就是在变化的状态中产生出来的，故有“动态”的含义，称这种解决多阶段决策最优化的过程为动态规划方法 。

基本思想

1. 动态规划(Dynamic Programming)算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
2. 动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
3. 与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。(即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)
4. 动态规划可以通过填表的方式来逐步推进,得到最优解.。

动态规划算法的两种形式

上面已经知道动态规划算法的核心是记住已经求过的解，记住求解的方式有两种：①自顶向下的备忘录法 ②自底向上。

先看一个例题：求阶乘函数

n! = {
    1              n = 0
    n x (n - 1)!   n=> 1
        }
        
 int f(int n){
     if(n == 0 ){
         return 1 ;
     }else{
         return n * f(n - 1);
     }
 }       
    

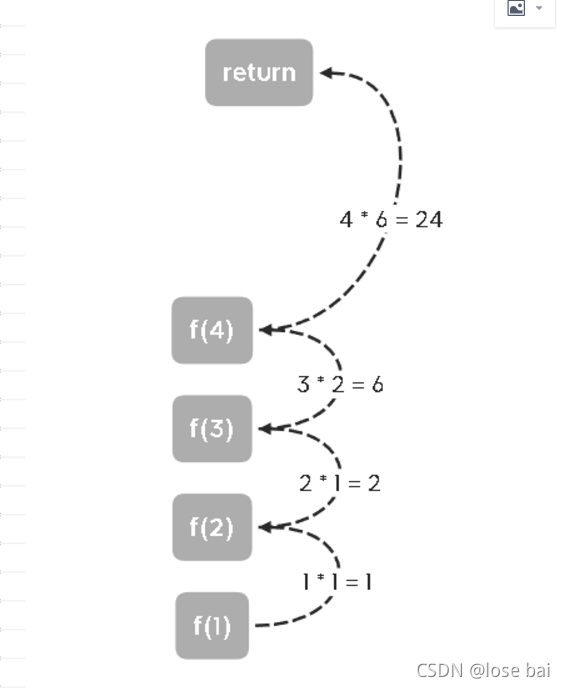
自顶向下的备忘录法

备忘录法就是创建一个容器，在递归的时候如果发现前面的值计算出来了就不再计算，如果未计算出来，则计算出来后保存在Men数组中，下次在调用fib（n）的时候就不会重新递归了

int factorial(n){
    int men[ 10 ]; // n 是一个包含 10 个整数的数组
   // 初始化数组元素          
   for ( int i = 0; i < 10; i++ )
   {
      men[ i ] = 0; 
   }
    return f(n, men)
}

int f(int n, int *men){
     if(n == 0 ){
        men[n] =  1 ;
     }else{
         men[n] = n * f(n - 1, men);
     }
     return men[n];
 } 

自底向上的动态规划

备忘录法还是利用了递归，ye 就是动态规划的核心，先计算子问题，再由子问题计算父问题。

int factorial(int n)
{
    if(n<=0)
        return n;
    int []Memo=new int[n+1];
    	Memo[0]=0;
    	Memo[1]=1;
    for(int i= 2;i<=n;i++)
    {
    	Memo[i] = i * i ;
    }		
    return Memo[n];
}

自底向上利用数组保存了先计算的值，为后面的调用服务

背包问题

例题：

1. 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品,如何选择物品放入背包使物品的价值最大。其中又分01背包和完全背包(完全背包指的是:每种物品都有无限件可用)
2. 这里的问题属于01背包,即每个物品最多放一个。而无限背包可以转化为01背包。
3. 算法的主要思想,利用动态规划来解决。每次遍历到的第i个物品,根据w[j]和v来确定是否需要将该物品放入背包中。即对于给定的n个物品,设vij、wj分别为第i个物品的价值和重量,C为背包的容量。再令vi]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:

推导公式：
v[i - 1][j - w[i]]: 上一个剩余的价值

v[i][i] = max {  v[i-1][j], v[i] + v[i - 1][j - w[i]] }

private static int[] w = {1, 2 ,3 ,4 ,5, 6, 7, 8};//物品的重量
private static int[] val = {1500, 2000, 2500,3000 ,3500,4000,4500,5000}; //物品的价值 这里val[i] 就是前面讲的v[i]
private static int m = 13; //背包的容量
private static int n = val.length; //物品的个数
private static int[][] v = new int[n + 1][m + 1]; 
// 行是物品 列是背包

    {
        for (int i = 0; i < v.length; i++) {
            v[i][0] = 0; //将第一列设置为0
        }
        for (int i = 0; i < v[0].length; i++) {
            v[0][i] = 0; //将第一行设置0
        }
    }

    /**
     * 根据前面得到公式来动态规划处理，组建表格，行是背包的容量，列是物品，其中的值是最大的价值
     */
    public static void dbHandler() {
        for (int i = 1; i < v.length; i++) { // 背包的容量
            for (int j = 1; j < v[0].length; j++) { //  物品

                if (w[i - 1] > j) { // 物品的重量大于背包的容量时， 会继承上一个物品的价值
                    v[i][j] = v[i - 1][j];

                } else {
                    int last = v[i - 1][j]; // 上一个物品的价值
                    int next = val[i - 1] + v[i - 1][j - w[i - 1]]; // 当前物品的价值 + 剩余背包的容量所在的价值

                    v[i][j] = Math.max(last, next);
                }
            }

        }

    }

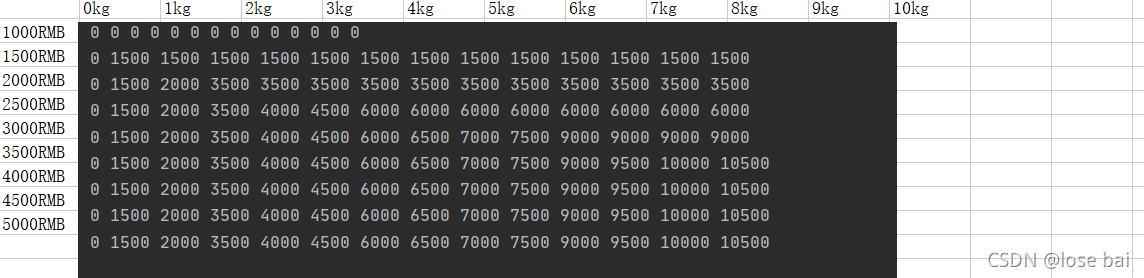
总结：

1. 最优子结构
   用动态规划求解最优化问题的第一步就是刻画最优解的结构，如果一个问题的解结构包含其子问题的最优解，就称此问题具有最优子结构性质。因此，某个问题是否适合应用动态规划算法，它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时，用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。
2. 重叠子问题
   如果递归算法反复求解相同的子问题，就称为具有重叠子问题（overlapping subproblems）性质。在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。

参考巨佬文章： https://blog.csdn.net/u013309870/article/details/75193592