[数据结构与算法]＜数据结构与算法＞-Python二叉搜索树

1 二叉树遍历

二叉树遍历分为四种方式，分别是前序遍历，中序遍历，后序遍历和层序遍历

• 前序遍历顺序 根->左->右
• 中序遍历顺序 左->根->右
• 后序遍历顺序 右->左->根
• 层序遍历顺序 按层遍历

遍历二叉树最好的方式是使用递归的方式

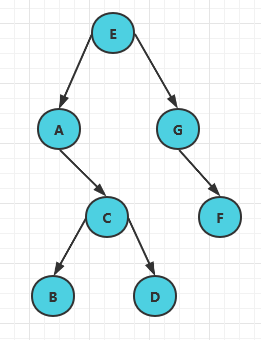
如上图所示的二叉树，可以使用如下方式：

class Node:
    def __init__(self,data):
        self.data = data 
        self.lchild = None 
        self.rchild = None 
        self.parent = None 


a = Node('A')
b = Node('B')
c = Node('C')
d = Node('D')
e = Node('E')
f = Node('F')
g = Node('G')


e.lchild = a 
e.rchild = g
a.rchild = c 
c.lchild = b 
c.rchild = d
g.rchild = f 


def pre_order(root):
    if root:
        print(root.data,end=',')
        pre_order(root.lchild)
        pre_order(root.rchild)


def in_order(root):
    if root:
        in_order(root.lchild)
        print(root.data,end=',')
        in_order(root.rchild)


def post_order(root):
    if root:
        post_order(root.rchild)
        post_order(root.lchild)
        print(root.data,end=',')


def level_order(root):
    from collections import deque
    q = deque()
    q.append(root)
    while len(q):
        node = q.popleft()
        print(node.data,end=',')
        if node.lchild:
            q.append(node.lchild)
        if node.rchild:
            q.append(node.rchild)

if __name__ == "__main__":
    pre_order(e)
    print("")
    in_order(e)
    print("")
    post_order(e)
    print("")
    level_order(e)

"""
OUT
前序遍历：E,A,C,B,D,G,F,
中序遍历：A,B,C,D,E,G,F,
后序遍历：F,G,D,B,C,A,E,
层序遍历：E,A,G,C,F,B,D,
"""

已知任意两种遍历结果，可以还原一颗树

• 知道前序和中序遍历结果

前序遍历：E,A,C,B,D,G,F,
中序遍历：A,B,C,D,E,G,F,

step1：前序遍历第一个结点肯定是根节点，得E是根节点
step2：中序遍历E左边的位置ABCD是左子树群，GF是右子树群
step3：前序遍历第二个结点是A，中序遍历第一个结点是A，说明A是E的左子树，G是E的右子树，第二层还原完成
step4：中序遍历第一个结点就是A，说明A没有左子树，C是A的右子树
step5：前序遍历CBD，中序遍历BCD，说明C的左子树是B，右子树是D
step6: F是G的右节点
根据不同遍历执行的顺序是可以还原整颗树的

2 二叉树搜索树

2.1 插入

新建一个结点

class BiTreeNode:
    def __init__(self,data):
        self.data = data 
        self.lchild = None 
        self.rchild = None 
        self.parent = None 

递归方式插入

class BiTree:
    def __init__(self,li=None):
        self.root = None 
        if li:
            for i in li:
                self.insert_no_rec(i)

    def insert(self,node,val):
        if not node: # 如果是一个空树
            node = BiTreeNode(val) # 新建结点，并且返回结点，这是一个递归终止条件
        elif val < node.data: # 如果插入的值小于node的值，那么往node的左子树方向找
            node.lchild = self.insert(node.lchild,val) # 递归
            node.lchild.parent = node  
        elif val > node.data: # 要插入的值大于node的值，那么往node的右子树方向找
            node.rchild = self.insert(node.rchild,val)
            node.rchild.parent = node 
        return node  
        

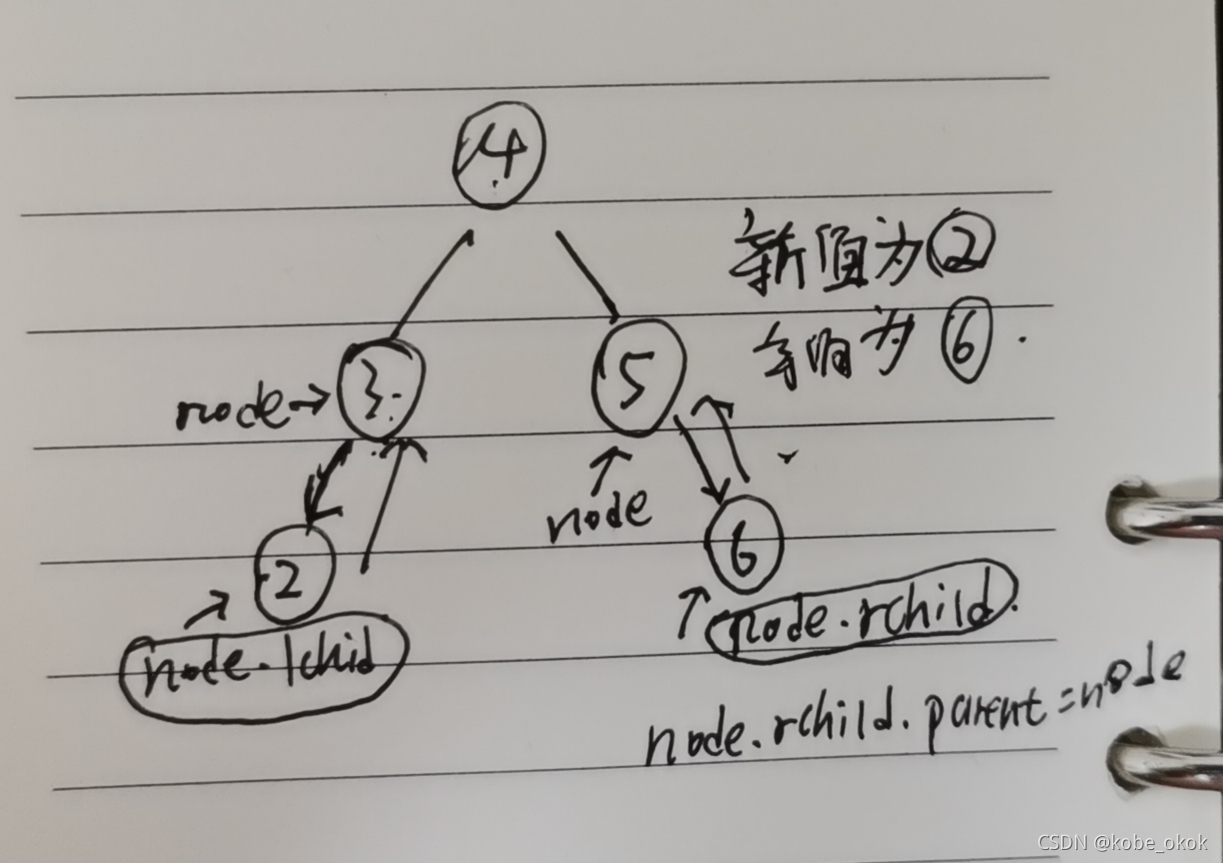
非递归方式插入

# class BiTree:
def insert_no_rec(self,val):
        curent = self.root #设置根结点为当前结点
        if not curent: # 如果是一颗空树
            self.root = BiTreeNode(val) # 设置根节点
            return # 退出函数
        while True: # 进入循环
            if val > curent.data: # 如果当前值大于node的值
                if curent.rchild: # 往当前结点的右孩子找
                    curent = curent.rchild 
                else: # 如果结点没有右孩子
                    curent.rchild = BiTreeNode(val) # 将值作为结点的右孩子插入
                    curent.rchild.parent = curent # 设置这个右孩子的结点
                    return  # 退出本函数
            elif val<curent.data: # 往左孩子找
                if curent.lchild:
                    curent = curent.lchild
                else:
                    curent.lchild = BiTreeNode(val)
                    curent.lchild.parent = curent
                    return 
            else: # 如果相等，直接退出，不进行任何操作
                return 

2.2 查询

#class BiTree:
    def select(self,val):
        p = self.root # 设置一个指针初始化为根结点
        if not p: # 空树没有任何值 
            return False #直接返回False 
        while True: 
            if val<p.data: #如果要查找的值小于结点的值
                if p.lchild: 
                    p = p.lchild # p结点往左一直到叶子结点还没找到就没有了，返回None 
                else:
                    return None
            elif val>p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    return None
            else:
                return p

2.3 删除

二叉搜索树的删除时比较复杂的，可以分为三种不同的情况

删除的结点时叶子结点，没有任何子节点，这种情况就直接删除掉

#class BiTree:
    def __remove_node_1(self,node):# 方式1：叶子结点
        if not node.parent:
            self.root = None 
        if node == node.parent.lchild: # 如果node是左孩子
            node.parent.lchild = None 
            node.parent = None # 这步可以省略
        else: #右孩子
            node.parent.rchild = None 
            node.parent = None 

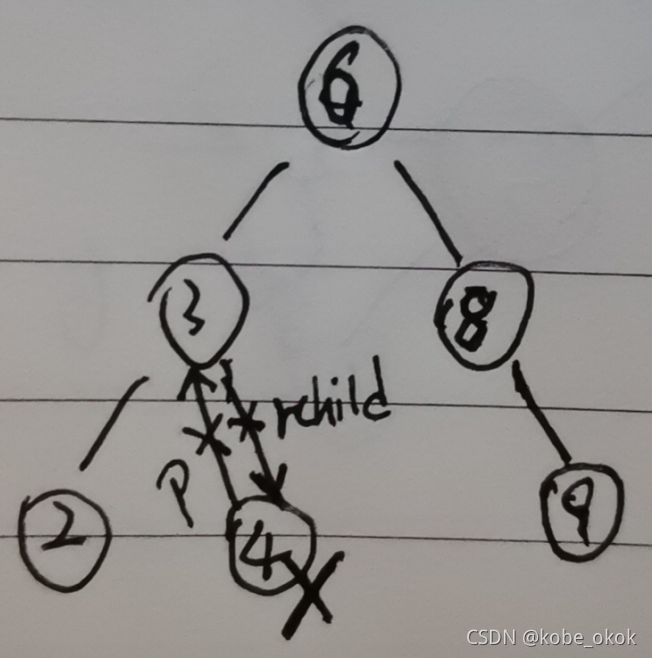
删除的结点有一个孩子，结点的父结点直接链接这个要删除结点的孩子结点

#class BiTree:
		def __remove_node_2_1(self,node): # 方式2-1：被删除的结点有一个左孩子
        if node == node.parent.lchild: # 被删除的结点是它父节点的左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent 
        else: # 被删除的结点时它父结点的右孩子
            node.parent.rchild = node.lchild 
            node.lchild.parent = node.parent
    

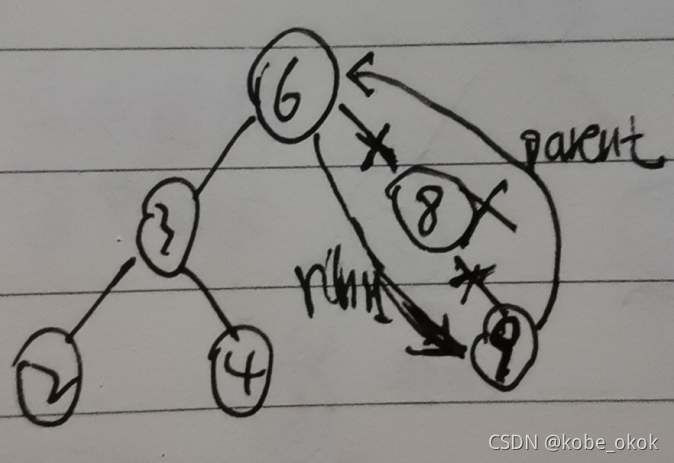
    def __remove_node_2_2(self,node): # 方式2-2：被删除的结点有一个右孩子
        if node == node.parent.lchild: # 被删除的结点是它父节点的左孩子
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent 
        else: # 被删除的结点时它父结点的右孩子
            node.parent.rchild = node.rchild 
            node.rchild.parent = node.parent

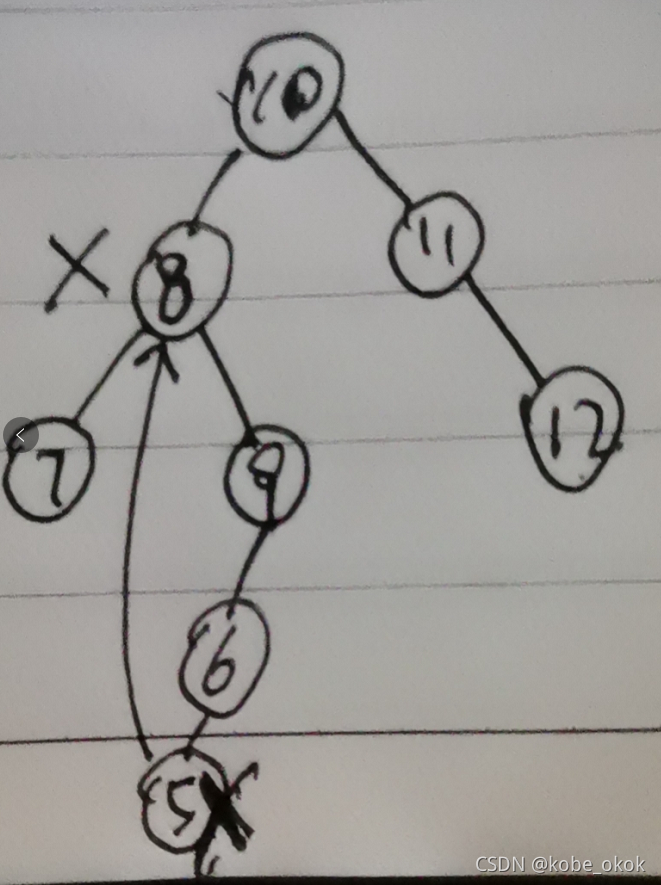
删除的结点是根节点，找到这个根节点右节点的最小子节点，与这个根节点替换掉，然后删除这个子节点

#class BiTree:
    def delete(self,val):
        node = self.select(val)
        if node:
            if not node.lchild and not node.rchild: # node没有左孩子也没有右孩子
                self.__remove_node_1(node)
            elif not node.rchild:#只有左孩子
                self.__remove_node_2_1(node)
            elif not node.lchild:
                self.__remove_node_2_2(node)
            else:
                min_node = node.rchild # 获取根的右节点作为最下结点
                while min_node.lchild: # 如果跟的右节点有左节点
                    min_node = min_node.lchild # 遍历一直到底
                node.data = min_node.data  # 使用右节点下面最小的子节点替换掉node的值
                self.__remove_node_1(min_node) # 移除掉最小子节点

3 附完整代码

class BiTreeNode:
    def __init__(self,data):
        self.data = data 
        self.lchild = None 
        self.rchild = None 
        self.parent = None 
    
class BiTree:
    def __init__(self,li=None):
        self.root = None 
        if li:
            for i in li:
                self.insert_no_rec(i)

    def insert(self,node,val):
        if not node:
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild,val)
            node.lchild.parent = node 
        elif val > node.data:
            node.rchild = self.insert(node.rchild,val)
            node.rchild.parent = node 
        return node  
        
        

    def insert_no_rec(self,val):
        curent = self.root
        if not curent: # 如果是一颗空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val > curent.data:
                if curent.rchild:
                    curent = curent.rchild
                else:
                    curent.rchild = BiTreeNode(val)
                    curent.rchild.parent = curent
                    return 
            elif val<curent.data:
                if curent.lchild:
                    curent = curent.lchild
                else:
                    curent.lchild = BiTreeNode(val)
                    curent.lchild.parent = curent
                    return 
            else:
                return 
                
    def in_order(self,root):
        if root:
            self.in_order(root.lchild)
            print(root.data,end=',')
            self.in_order(root.rchild)
                

    def pre_order(self,root):
        if root:
            print(root.data,end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)


    def post_order(self,root):
        if root:
            self.post_order(root.rchild)
            self.post_order(root.rchild)
            print(root.data,end=',')
    

    def level_order(self,root):
        from collections import deque
        q = deque()
        q.append(root)
        while len(q) > 0:
            node = q.popleft()
            print(node.data,end=',')
            if node.lchild:
                q.append(node.lchild)
            if node.rchild:
                q.append(node.rchild)
        

    def select(self,val):
        p = self.root
        if not p: # 空树没有任何值
            return False 
        while True:
            if val<p.data:
                if p.lchild:
                    p = p.lchild
                else:
                    return None
            elif val>p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    return None
            else:
                return p
    

    def __remove_node_1(self,node):# 方式1：叶子结点
        if not node.parent:
            self.root = None 
        if node == node.parent.lchild: # 如果node是左孩子
            node.parent.lchild = None 
            node.parent = None # 这步可以省略
        else: #右孩子
            node.parent.rchild = None 
            node.parent = None 


    def __remove_node_2_1(self,node): # 方式2-1：被删除的结点有一个左孩子
        if node == node.parent.lchild: # 被删除的结点是它父节点的左孩子
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent 
        else: # 被删除的结点时它父结点的右孩子
            node.parent.rchild = node.lchild 
            node.lchild.parent = node.parent
    

    def __remove_node_2_2(self,node): # 方式2-2：被删除的结点有一个右孩子
        if node == node.parent.lchild: # 被删除的结点是它父节点的左孩子
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent 
        else: # 被删除的结点时它父结点的右孩子
            node.parent.rchild = node.rchild 
            node.rchild.parent = node.parent



    def delete(self,val):
        node = self.select(val)
        if node:
            if not node.lchild and not node.rchild: # node没有左孩子也没有右孩子
                self.__remove_node_1(node)
            elif not node.rchild:#只有左孩子
                self.__remove_node_2_1(node)
            elif not node.lchild:
                self.__remove_node_2_2(node)
            else:
                min_node = node.rchild # 获取根的右节点作为最下结点
                while min_node.lchild: # 如果跟的右节点有左节点
                    min_node = min_node.lchild # 遍历一直到底
                node.data = min_node.data  # 使用右节点下面最小的子节点替换掉node的值
                self.__remove_node_1(min_node) # 移除掉最小子节点