系列文章目录
文章目录
前言
笔记来源于视频(侵删):
一、查找


二分查找要求列表有序

二、排序


总结:
-
冒号排序:遍历n-1趟,每次两两交换,原地排序。外层循环为for i in range(len(li)),内层循环为for j in range(len(li)-1-i)。可以通过加一个判断(如果这一趟中没有发生交换,则说明已经全部排好序,终止循环)进行优化
-
选择排序:遍历一遍列表,选择最小的值,放到新列表中,遍历n遍。
-
插入排序:假定手里的牌已经有序,然后插入。即从第二个数开始遍历n-1趟,每次将当前的数与前面已经排好的数进行比较,将其插入到合适的位置。外层循环为for i in range(1,len(li)),令j=i-1,则内层循环为while tmp<li[j] and j >=0,即当升序排列时,当当前数tmp小于前一个数的时候就把前一个数往后挪,即令li[j] = li[j-1],j =j-1
-
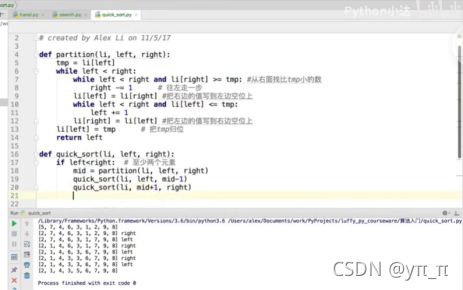
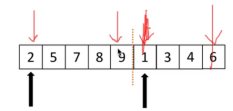
快排:选择第一个数tmp,使其左边的数小于tmp,右边的数大于tmp。参数为left、right、li:先往前从right开始遍历找到比tmp小的数,把它放到li[left]位置上,因为将第一个数tmp取出后左边有空位;然后在从left开始往后遍历,找到比tmp大的数,把它放到li[right]上,因为之前取出了right位置上的数,所以有空位,做循环,最后把tmp归位即可。然后做递归,左右两边分别递归,每次循环问题减半。
-
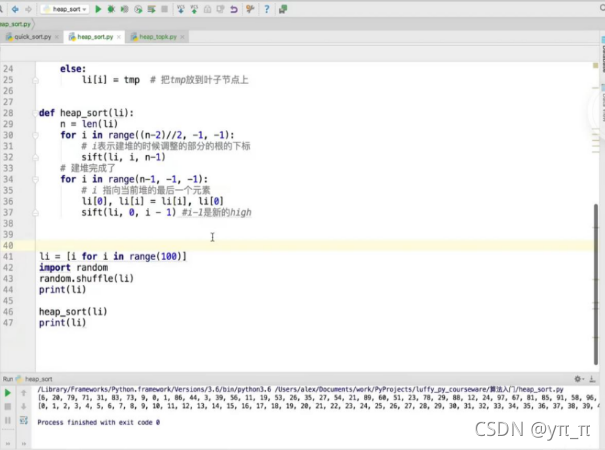
堆排序:
-
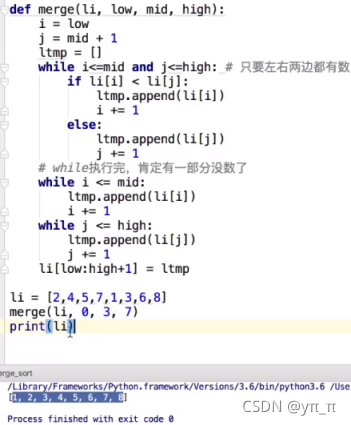
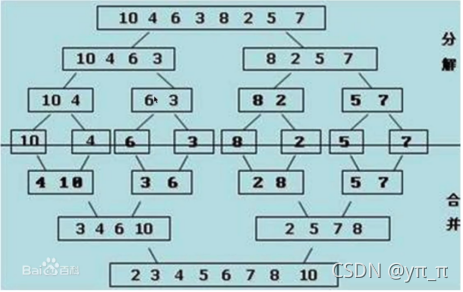
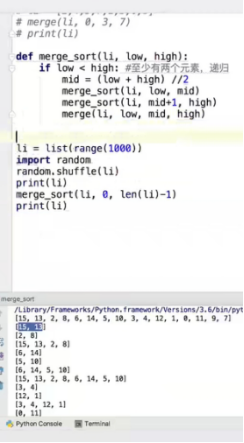
归并排序:假设两边分别有序,把两边合到一起使其整体有序。参数为low,mid,high,li:令i=low,j=mid+1,tmp=[],当升序排列时,当左右两边都有数的时候:依次比较li[i]和li[j]的大小,选择小的一个添加到tmp列表中去;当只有一端有数的时候,直接将剩下的数全部添加到tmp列表后面去,因为剩下的数是有序且大于之前添加的数的。然后做递归:当low<high,即最少有两个数的时候,先求出中间值mid,然后左右分别做递归,递归之后再对最小层的数做排序。
插入排序:

快排:
堆排序:



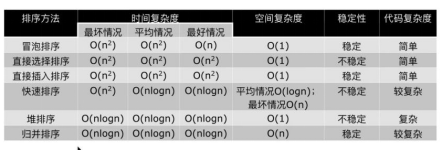
时间复杂度:
- O(1):执行一次基本操作的时间(近似),1是指1个单位(不看到底执行了几次,只要不上升到n次的时候 就是O(1))
- O(n^2):当是n的(2+n)次方时,只保留大的即可,只需大概的时间即可,不需要很精确。
- O(logn):当出现循环减半时,(即每次迭代让问题规模缩小一半)
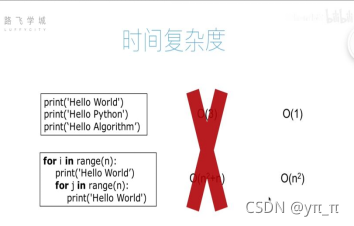



时间比空间重要。

1、冒号排序
需要n-1趟排序

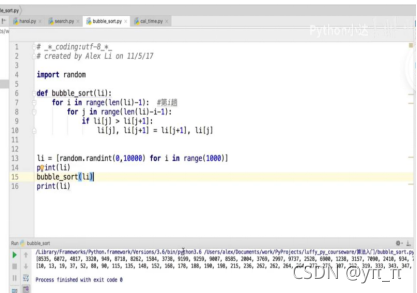

2、选择排序
遍历一遍列表,选择最小的值,放到新列表中,遍历n遍。
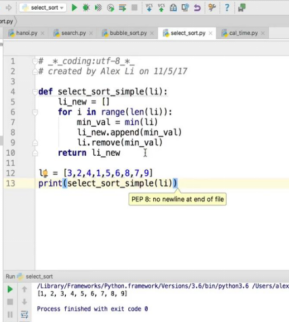
缺点:
- 占用了两倍内存,不是原地排序(冒号排序是原地排序),
- 时间复杂度为O(n^2)
- min函数的时间复杂度为O(n)(因为找列表最小值时,需要遍历列表,所以时间复杂度不是O(1)),remove函数的时间复杂度也是O(n)(因为删除列表中的某个数字后,需要将后面的数字依次往前移一位,否则会造成一个空位),所以整个算法的时间复杂度为O(n^2)(循环里面的两个O(n)记为一个)
优化:时间复杂度O(n^2)
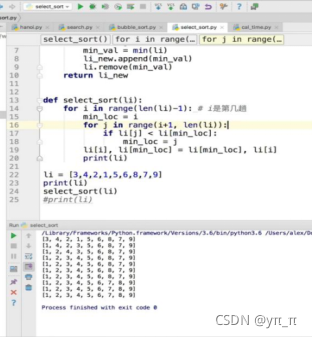
3、插入排序


4、快速排序

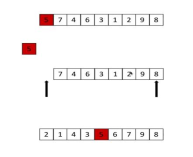
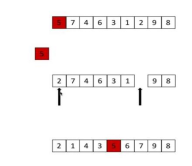
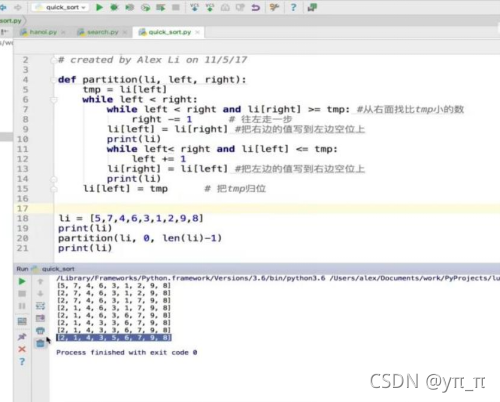


时间复杂度:
-
每一层的partition的复杂度是O(n),一共logn层,所以时间复杂度为O(nlogn)
-
最坏情况:传入的列表为倒序,每次partition只变动一个值,则就不是logn层
优化:
- 加入随机划分,即随机选择一个数,将其与第一个位置的数进行交换,然后再对其进行归位,会降低出现最坏情况的概率。
5、堆排序
堆排序时间复杂度是nlog(n)级别,和快速排序一样,但是在实际执行时,快排要快于堆排序
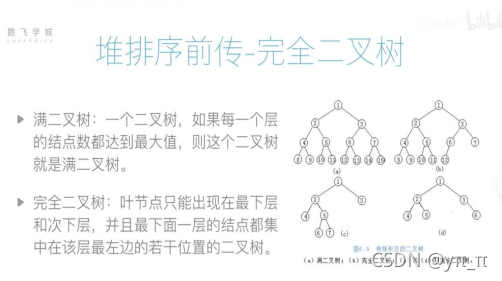
1、树与二叉树
 度:节点的分叉数
度:节点的分叉数
树的度= 整个树的最大的节点的度
E的度为2,F的度为3,
最大节点为A, 度为6,所以整个树的度为6
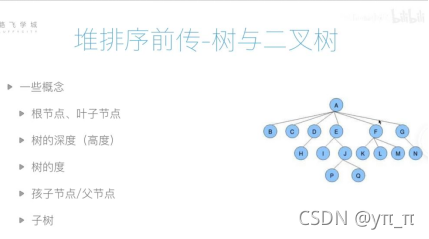


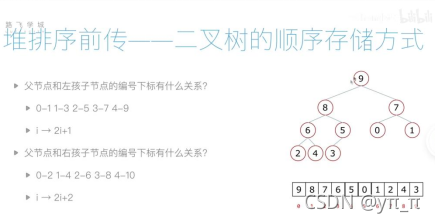
由子节点找父节点:
- 设子节点下标为i,则父节点为(i-1)//2
2、堆

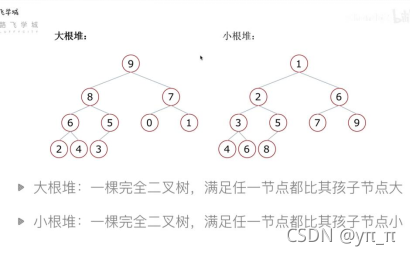
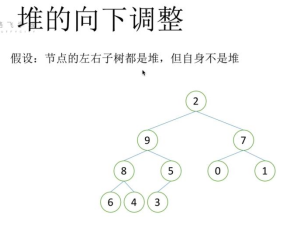
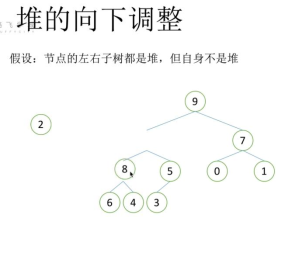
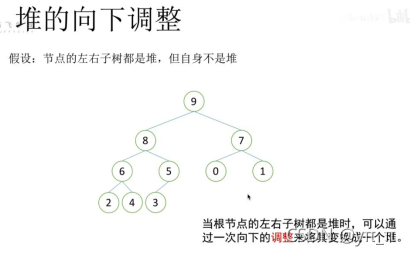
2.1 堆的向下调整性质

堆的向下调整性质:
- 1)在9和7(2的两个子节点)中进行比较,选择大的一个放到根节点(原2的位置)处
- 2)比较2与8、 5(两个子节点)的大小,发现2小于子节点,继续向下调整,

2.2 堆挨个出数的过程
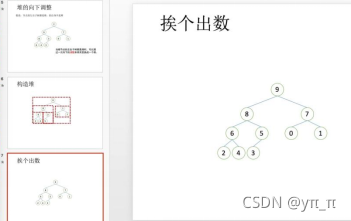
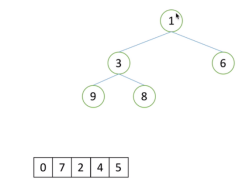
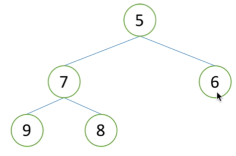
挨个出数过程(以大根堆为例):
- 1)出9
- 2)将3放到堆顶(根节点)(3为最后一个叶子结点)
- 3)对3进行向下调整,恢复成大根堆
- 4)出8(根节点),将最后一个叶子结点放到堆顶,进行向下调整
- 5)继续上述过程,直到所有数字出完
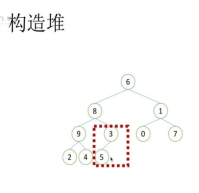
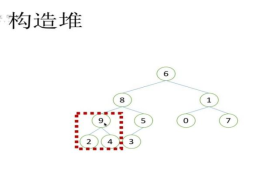
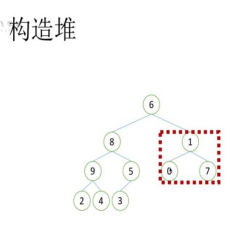
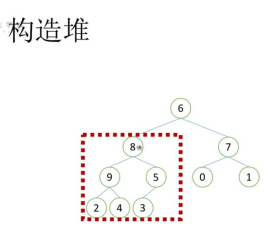
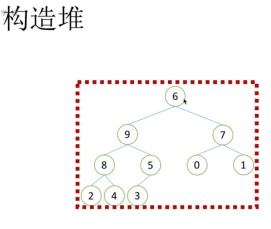
2.3 构造堆
1)找到最后一个非叶子节点,比较父节点和子节点的大小,使父节点大于子节点
2)调整倒数第二个非叶子节点,
2.4 堆排序算法


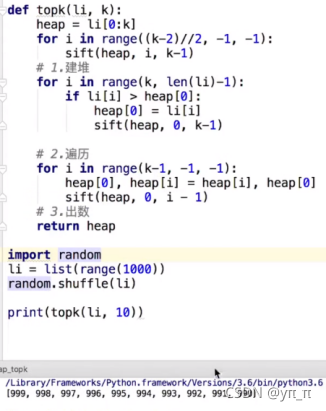
2.5 堆排序的应用:topk问题




6、归并排序



7、希尔排序



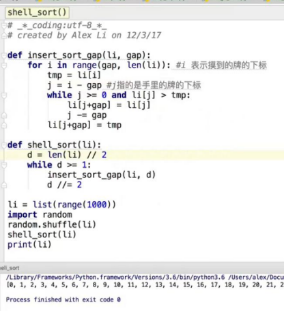

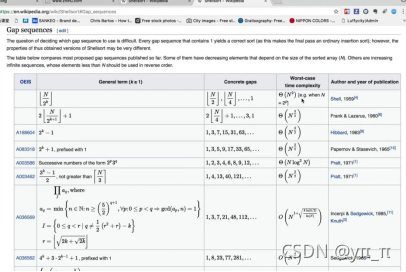
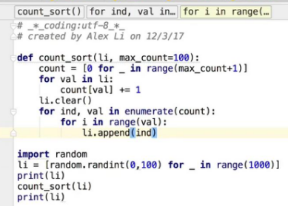
8、桶排序

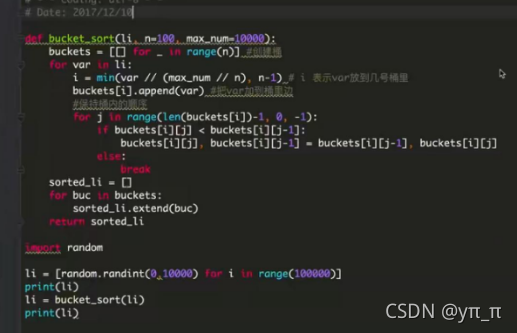

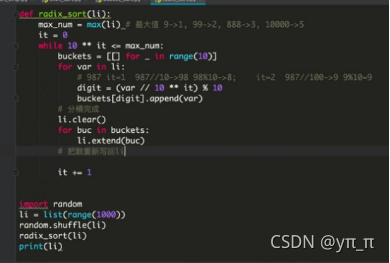
9、基数排序