1. DFS概念
通俗一点就是不撞南墙不回头。是一个递归的过程。
数据结构中的定义:假设初始状态是所有顶点未曾被访问,则深度优先搜索可从
图中某个顶点v0出发,访问此顶点,然后依次从v0的邻接点出发递归的进行同样
的深度搜索,直到图中所有和v0有路径相通的顶点都被访问到。好像还是很抽象,
那上图吧。

假设从E点出发,当有多种选择时,采用字母序的策略选取下一个邻接点。
选择A为下一个邻接点,则从A出发进行递归搜索。依此类推,依次从B,C,D出发进行递
归搜索。在访问了D之后,由于D的邻接点都被访问过了,则搜索回退(递归返回调用)
到C。由于同样原因,搜索继续回退到B,A,E。此时E有未访问过的邻接点,F开始
再访问G,H。再从H回退到G,G回退到F,F最后回退到E。这就完成了一个连通分量的搜
索。
2.经典迷宫问题
杭电1010 http://acm.hdu.edu.cn/showproblem.php?pid=1010
题目大意:
意思就是给定一个由字符组成的迷宫,‘S’代表起点,‘.'代表可以通行的块,’X‘代表
一堵墙,’D‘代表终点。每秒只能走一步(上,下,左,右),判断能否在恰好第T秒,
到达终点D,走过的块不能再走。
算法就是dfs了,其实也就是暴力枚举,对走的每一步都进行4个方向上的分支判断,
对选中的分支然后进行递归搜索,再加上一定的剪枝,舍去一些明显不合题意的结果,
以满足时间上的要求。
#include <iostream>
#include <cstdlib>//abs函数的头文件
using namespace std;
char map[8][8];//迷宫
int d[4][2]={{0,1},{1,0},{0,-1},{-1,0}};//往东南西北
//方向走时x,y需要加上的值
int dfs(int sx,int sy,int cnt);
int sx,sy,ex,ey,N,M,T,value;
int ok=0;
int main()
{
int wall,i,j;
while(cin>>N>>M>>T){
ok=0;
if(N==0&&M==0&&T==0) break;
wall=0;
for(i=1;i<=N;i++){
for(j=1;j<=M;j++){
cin>>map[i][j];
if(map[i][j]=='S'){
sx=i;
sy=j;
}
else if(map[i][j]=='D'){
ex=i;
ey=j;
}
else if(map[i][j]=='X'){
wall++;//不可到达的块数加1
}
}
}
if((N*M-wall-1)<T){//可以走的步数小于T
cout<<"NO"<<endl;
continue;
}
map[sx][sy]='X';//起点设为不可达
dfs(sx,sy,0);
if(ok) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
int dfs(int sx,int sy,int cnt){
//cout<<"cnt="<<cnt<<endl;
if(sx<=0||sy<=0||sx>N||sy>M){//递归终止条件 ,超出边界
return 0;
}
int temp=T-cnt-(abs(sx-ex)+abs(sy-ey));//
if(temp<0||temp&1){//奇偶剪枝,temp小于0或为奇数则不可达
return 0;
}
if(sx==ex&&sy==ey&&cnt==T) ok=1;//
if(ok==1) return 1;
for(int i=0;i<4;i++){//对走到的每个结点进行四个方向的探索
if(map[sx+d[i][0]][sy+d[i][1]]!='X'){
map[sx+d[i][0]][sy+d[i][1]]='X';//走过的路,不能再走,设为墙
value=dfs(sx+d[i][0],sy+d[i][1],cnt+1);
if(value==1) break;//到达终点了
map[sx+d[i][0]][sy+d[i][1]]='.';//探索一条路不可达,return 0后
//探索下一条路时 ,这个节点要恢复为可走状态
}
}
return 0;
}
一个小技巧初始化这个迷宫矩阵的时候,i = 0 这行, j = 0这列, i = n + 1这行, j = m + 1这列,也就是最外层初始化为0,但是不存储数据,这样相当于在迷宫外面的四面都加上了墙,这样在dfs过程中就不用判断是否出界了…
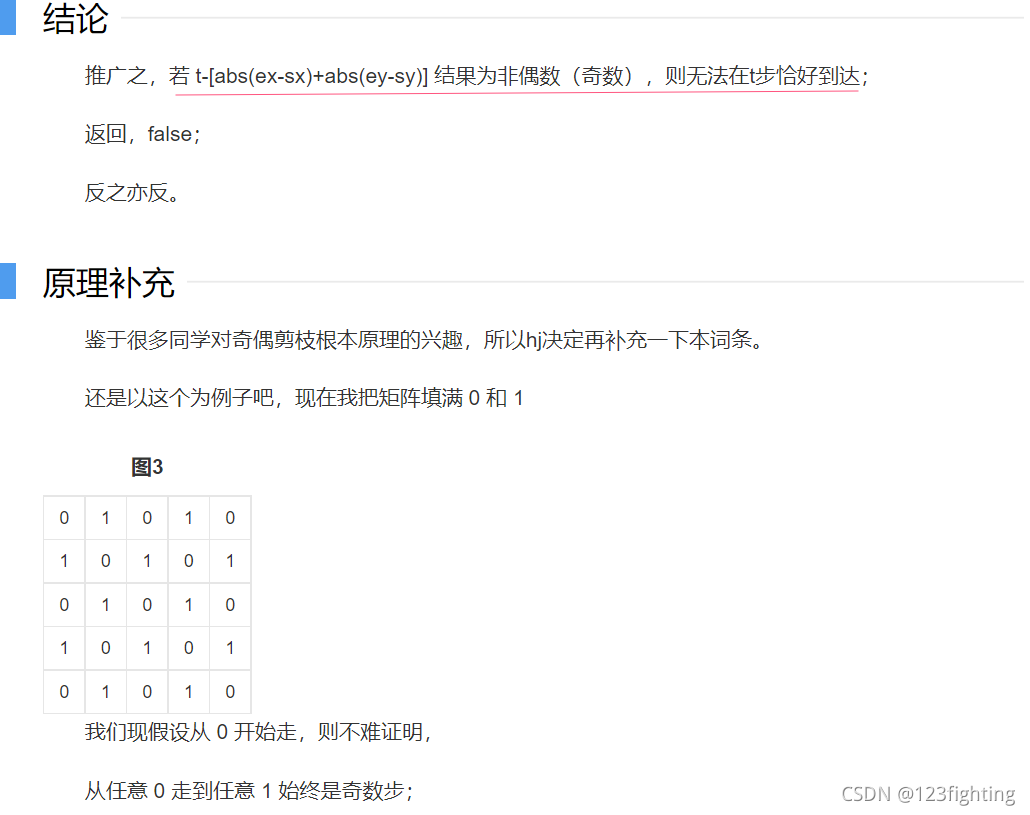
3.奇偶剪枝
从百度百科截图过来的,百度百科上有点错误。奇偶剪枝其实就是给定t步到达终点,这t步减去到达终点的最短路径必须要为偶数的情况。