这段时间做到一题算法题,感觉挺有意思的,拿来分享一下思路
题目:
假如对二叉树T和具有相同高度的满二叉树编号,如果T与满二叉树相同编号的节点位置相同,那么称二叉树T是一棵完全二叉树。现在根据边的连接情况判断一棵树是否是完全二叉树。
输入:
第一行有2个整数n(0 < n < 1024)和r(1<=r<=n), 表示结点数和树根,接下来n-1行每行有2个整数a,b (1 <= a,b <= n)表示a结点和b结点有一条边相连,如果a是b的根结点,则b是a的左子结点,如果b是a的根结点,则a是b的右子结点(数据保证是一棵树而不是一座森林)
输出:
如果是完全二叉树 输出yes 否则输出no
思路:
首先要清楚什么是完全二叉树,一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。也就是说这个二叉树,他是从上到下从左到右排的。
完全二叉树有一些重要的性质,比如左子树等于本身*2,右子树等于本身*2+1等,因为这边我没用到就不仔细讲了
我们先观察一下这两个完全二叉树
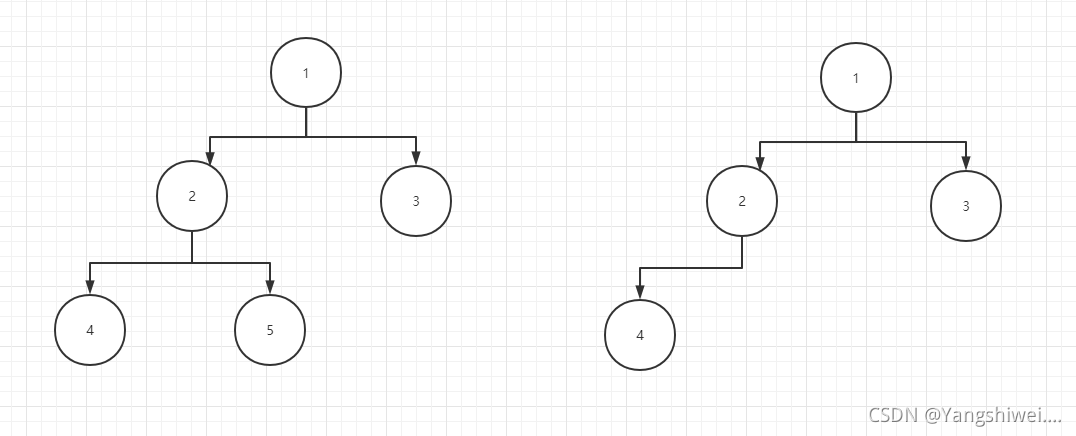
我们可以看到,完全二叉树在最底下的一排都只有一条连线(比如3,4,5),而其他结点都有至少两个连线,且以3为分界线,3之前都至少有2跟连线,而之后只有1个。
我们还可以观察到,根结点都只有两个连线,且总结点数为?奇数(如左图)的二叉树,除根节点外连线非3即1,为偶数(如右图),除根节点外,在中间有一个结点连线也为2,在其之前都为3,之后都为1.。
于是我们可以用数组做这题
这是我的代码,我先判断了他n的个数,即是左图还是右图的情况,再根据他们不同的情况来执行判断(其实我这里代码写长了,他们的前后都是一样的,只要在中间加入个是否==2的判断即可)
public class main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int r = scanner.nextInt();
int arr[] = new int[n + 1];
arr[r] = 1;
for (int i = 1; i < n; i++) {
int a = scanner.nextInt();
int b = scanner.nextInt();
arr[a]++;
arr[b]++;
}
if (n % 2 == 0) {
int i = 1;
for (; i <= n; i++) {
if (arr[i] != 3) {
break;
}
}
if(arr[i] != 2){
System.out.println("no");
return;
}
i++;
for(;i<=n;i++){
if (arr[i] != 1) {
System.out.println("no");
return;
}
}
System.out.println("yes");
return;
} else {
int i = 1;
for (; i <= n; i++) {
if (arr[i] != 3) {
break;
}
}
for(;i<=n;i++){
if (arr[i] != 1) {
System.out.println("no");
return;
}
}
System.out.println("yes");
return;
}
}
}