[数据结构与算法]最长回文子串+最长回文子序列

两道经典的动态规划题

最长回文子序列
最长回文字串

基础概念

回文 (Palindrome)

回文，指正读反读都能读懂的句子，如“我为人人，人人为我”等。在数学中也有这样一类数字有这样的特征，称为回文数（palindrome number），如n=1234321,则n为回文数。

回文字符串:即"aba","ccc"这种正读反读都相同的字符串

字串和子序列

子串：新字符串是原字符串中连续的一部分。
子序列：新字符串不一定是原字符串中连续的，可能缺失了中间的某个或某些字符。
例：如"asdfgh"
子串：“asd"或"fgh”，字符连在一起，且是原字符串中的一部分
子序列：“afh”，字符不一定连在一起，但每个字符都属于原字符串，且有序。

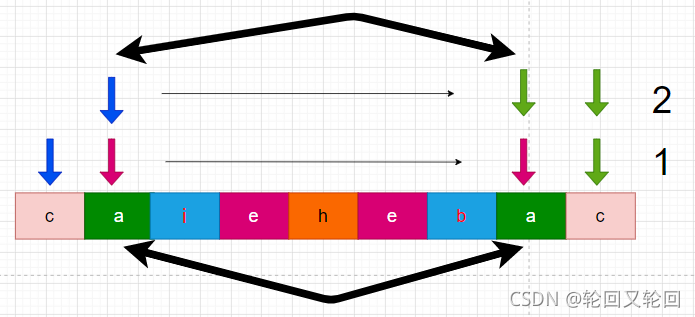
如何验证是否是回文串？

首先验证字符串的第一个字符和最后一个字符。
1）如果这两个字符不相同，则这个字符串一定不是回文串。
2）如果这两个字符相同，则继续验证起点的下一个字符以及终点的上一个字符，不断验证下去。
不断的更新起点字符和终点字符，直到起点位置大于等于终点位置，结束验证，证明整个字符串是回文串。

一旦在验证过程中有字符不相同，说明整个字符串都不是回文串

代码：

//递归
public boolean longestPalindrome(String s){
	int n = s.length();
	return checkPalindrome(s,0,n-1);
}

public boolean checkPalindrome(String s, int start, int end){
	if(start >= end){
		return true;
	}
	if(s.charAt(start)==s.charAt(end){
		return help(s,start+1,end-1);
	}
	return false;
}

leetcode5：最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

解法一：暴力解法-递归

暴力解法：当以前字符作为起点，终点字符在不断变化，验证每个子串是否是回文串。依次将每个字符作为起点字符，重复上述操作，并且记录最大长度的回文串。

int start;
int len;
public boolean longestPalindromeSubstring(String s){
	int n = s.length();
	start = 0;
	len = 0;
	for(int i = 0; i < n; i++){	
		for(int j = i; j < n; j++){
		//验证第i个字符到第j个字符组成的字符串是否是回文串
		//如果是回文串，则验证是否更新了已记录的最长记录
			if(checkPalindrome(s,i,j)){
				if(j-i+1 > len){
					len = j - i + 1;
					start = i;
				}
			}
		}	
	}
	return s.substring(start,start+len);
}

暴力解法的时间复杂度为O(n^2)，虽然复杂度还可以，但是仍可以优化。

解法二：递归+剪枝化

我们可以设置一个记忆集(memory)，来记录第i个字符到第j个字符是否是回文串。这样当检查字串时，先检查memory，如果有记录就返回。没有再去递归检查。

class Solution {
    Integer[][] memory;
	public String longestPalindrome(String s){
		int n = s.length();
		int start = 0;
		int len = 0;
        memory = new Integer[n][n];
		for(int i = 0; i < n; i++){	
			for(int j = i; j < n; j++){
			//验证第i个字符到第j个字符组成的字符串是否是回文串
			//如果是回文串，则验证是否更新了已记录的最长记录
				if(checkPalindrome(s,i,j)){
					if(j-i+1 > len){
						len = j - i + 1;
						start = i;
					}
				}
			}	
		}
		return s.substring(start,start+len);
	}
	public boolean checkPalindrome(String s, int begin, int end){
		if(begin >= end){
			return true;
		}
		//记忆集中是否有记录
		if(memory[begin][end] != null){
			return memory[begin][end] == 0 ? false : true;
		}
		if(s.charAt(begin)==s.charAt(end)){
			//是回文串
            if(checkPalindrome(s,begin+1,end-1)){
                memory[begin][end] = 1;
                return true;
            }
            //不是回文串
			memory[begin][end] = 0;
			return false;
		}
		memory[begin][end] = 0;
		return false;
	}	
}

解法三：动态规划