[数据结构与算法]在二叉树中寻找快乐c++

??经典二叉树问题，快乐是要保证的。

二叉树的最大深度

??典中典之二叉树最大深度，非常经典的深度搜索和递归。
??对左右子树深度搜索，如果碰到空节点就返回，每次返回计数都+1，最后在左子树和右子树中取最大值。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root==nullptr) return 0;
        return max(maxDepth(root->left),maxDepth(root->right))+1;
    }
};

对称二叉树

??如果是判断对称的话，其实是迭代的思路比较好想。

class Solution {
public:
    bool mirrorTest(TreeNode* u,TreeNode* v){
        queue<TreeNode*> queue1;
        queue1.push(u);
        queue1.push(v);
        while(!queue1.empty()){
            u=queue1.front();
            queue1.pop();
            v=queue1.front();
            queue1.pop();
            if(u==nullptr&&v==nullptr) continue;
            if((!u||!v)||(u->val!=v->val)) return false;//如果其中一个不存在，或者值不相同就返回错误
            queue1.push(u->left);//左左和右右比
            queue1.push(v->right);
            queue1.push(u->right);//左右和右左比
            queue1.push(v->left);
        }
        return true;
    }
    bool isSymmetric(TreeNode* root) {
        return mirrorTest(root,root);
    }
};

??我们再使用一下深度搜索：

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        return compare(root->left,root->right);
    }
    bool compare(TreeNode* node1,TreeNode* node2){
        if(node1==nullptr&&node2==nullptr){//如果到了叶子节点
            return true;//返回可以，毕竟没得比了
        }
        if(node1==nullptr||node2==nullptr||node1->val != node2->val){//如果两者只有一个或者值不同，那就是不对称了
            return false;
        }
        return compare(node1->left,node2->right)&&compare(node1->right,node2->left);//注意递归时给子节点的配对
    }
};

翻转二叉树

??翻转二叉树是一个经典的前序遍历递归，是从根节点向下递归的。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr) return nullptr;//结束条件 如果到了空节点就返回空
        swap(root->left,root->right);//左右交换
        invertTree(root->left);//从根节点向下递归
        invertTree(root->right);
        return root;
    }
};

二叉树的直径

??这个直径题容易让人摸不清头脑。
??首先这个最大直径应该是时刻更新的，所以关键在于直径怎么表达。
??某个节点的直径等于该节点左子树的高度 + 右子树的高度。
??问题一下子分解成了：求每个点的高度+计算直径更新答案。

class Solution {
public:
    int res = 0; 
    int dfs(TreeNode* root){
        if(root == nullptr){//到空节点返回高度0
            return 0;
        }
        
        int left = dfs(root->left);//求该节点的左高度
        int right = dfs(root->right);//求该节点的右高度
        res = max(res,left+right);//更新直径，直径这个东西不是递归的，高度是递归的
        
        return max(left,right) + 1;//返回该节点的高度（左右取最高者）并+1
    }

    int diameterOfBinaryTree(TreeNode* root) {
        dfs(root);
        return res;
    }
};

剑指 Offer 27. 二叉树的镜像

??其实和翻转二叉树是一个题。

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) {
        if(root == NULL) return NULL;
        swap(root->left,root->right);//前序遍历
        mirrorTree(root->left);
        mirrorTree(root->right);
        return root;
    }
};

平衡二叉树

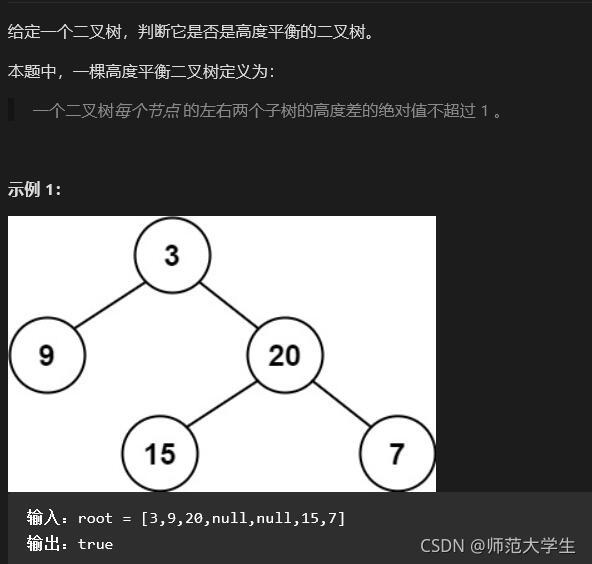
??平衡二叉树还是比较有意思的，说白了，对于任何一个节点来说，该节点的左右子树高度差不能超过1，而且左右子节点都应该满足这个条件。
??这条件也太递归了，同时我们注意这里要求节点的高度，这个求高度和判断平衡二叉树是无耦合的，我们可以拆出来写。

class Solution {
public:
    int getheight(TreeNode* node){//用来计算该节点的高度
        if(node == nullptr) return 0;
        return max(getheight(node->left),getheight(node->right)) + 1;
    }

    bool isBalanced(TreeNode* root) {
        if(root==nullptr){
            return true;
        }
        return abs(getheight(root->left)-getheight(root->right)) <=1&&isBalanced(root->left)&&isBalanced(root->right);    
    }
};

合并二叉树

??合并二叉树算是比较有趣的问题了，当然一看就知道是递归。
??注意我们要合并一个新的二叉树，也就是说每个节点在递归的时候，我们要为它创建一个新节点。
??我们这次用递归三部曲来想一下。
??终止条件是什么？当两个二叉树对应节点有空的时候返回另外一个。
??每一次递归return什么？因为我们每次递归到一个节点都要创建一个新节点，所以我们每次要把这个新节点给返回来。
??每一次递归操作什么？创建一个新节点，赋值，这还没完，需要为其配上左子节点和右子节点，配左子节点和右子节点就实现了递归。

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1==nullptr) return root2; //如果一个空了就返回另一个
        if(root2==nullptr) return root1;

        TreeNode* node = new TreeNode(0);//新建一个新节点
        node->val = root1->val + root2->val;//节点赋值
        
        node->left = mergeTrees(root1->left,root2->left);//递归，为新节点得到左右子节点
        node->right = mergeTrees(root1->right,root2->right);

        return node;//返回新节点
    }
};

二叉树的所有路径

??从这个题开始出现了“路径”一词。
??刷题有经验就会意识到，是不是该搜索了。
??再仔细一看提供的标准输入输出，完全可以确定是个深度优先搜索问题。

class Solution {
public:
    void dfs(TreeNode* root,vector<string>& res,string temp){
        if(temp==""){//根据不同的情况在字符串变量里加入不同成分
            temp += to_string(root->val);
        }else{
            temp +="->";
            temp += to_string(root->val);
        } 
        if(root->left==nullptr&&root->right==nullptr){//如果到了叶子节点就装答案
            res.push_back(temp);//注意要先加入到字符串里面
            return;
        }
        if(root->left) dfs(root->left,res,temp);
        if(root->right) dfs(root->right,res,temp);
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        if(root==nullptr) return result;

        dfs(root,result,"");//深度优先搜索
        return result;
    }
};

剑指 Offer 68 - II. 二叉树的最近公共祖先

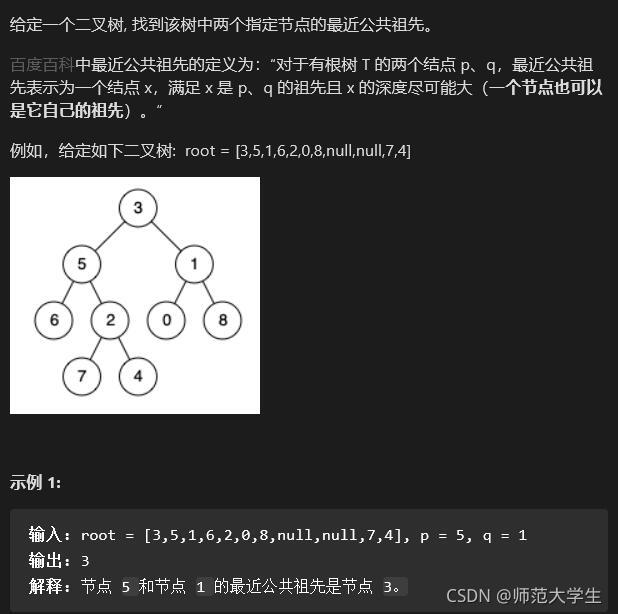
??我们要找两个节点的祖先，是不是应该从底往上找？所以该题是明显的后序遍历。
??清楚是后续遍历之后，我们去模拟寻找p和q的过程。
??如果寻找到了q或者p，就立刻返回，因为我们要祖先，肯定要上找。。
??如果该节点不是p或者q，就利用后序遍历从左右子树中去寻找，再根据左右子树寻找结果来判断公共祖先应该是自己，还是在左子树，还是在右子树。

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL||root == p||root == q){//如果该节点是q或者p，就将该节点返回
            return root;
        }
        //没找到，该节点不是p或者q，就从子树去找
        TreeNode* left = lowestCommonAncestor(root->left,p,q);//经典后续遍历，看左边右边谁能找到p或q
        TreeNode* right = lowestCommonAncestor(root->right,p,q);
        if(!left) return right; //左边为空，则都在右边，右边第一个找到的节点就为答案，注意这里不是ifelse关系，因为左右都要判断
        if(!right) return left; //右边为空，则都在左边，左边第一个找到的节点就为答案
        return root; //一边一个，则root是答案
    }
};