72. 编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
动态规划
题目给定了两个单词,设为 A 和 B,这样我们就能够六种操作方法。
但我们可以发现,如果我们有单词 A 和单词 B:
- 对单词
A删除一个字符和对单词B插入一个字符是等价的。例如当单词A为doge,单词B为dog时,我们既可以删除单词A的最后一个字符e,得到相同的dog,也可以在单词B末尾添加一个字符e,得到相同的doge; - 同理,对单词
B删除一个字符和对单词A插入一个字符也是等价的; - 对单词
A替换一个字符和对单词B替换一个字符是等价的。例如当单词A为bat,单词B为cat时,我们修改单词A的第一个字母b -> c,和修改单词B的第一个字母c -> b是等价的。
这样以来,本质不同的操作实际上只有三种:
- 在单词
A中插入一个字符; - 在单词
B中插入一个字符;- 修改单词
A的一个字符。
- 修改单词
我们用 D[i][j] 表示 A 的前 i 个字母和 B 的前 j 个字母之间的编辑距离。
D[i][j-1]为A的前i个字符和B的前j - 1个字符编辑距离的子问题。即对于B的第j个字符,我们在A的末尾添加了一个相同的字符,那么D[i][j]最小可以为D[i][j-1] + 1;D[i-1][j]为A的前i - 1个字符和B的前j个字符编辑距离的子问题。即对于A的第i个字符,在A的末尾删除i,那么D[i][j]最小可以为D[i-1][j] + 1;D[i-1][j-1]为A前i - 1个字符和B的前j - 1个字符编辑距离的子问题。即对于B的第j个字符,我们替换A的第i个字符使它们相同,那么D[i][j]最小可以为D[i-1][j-1] + 1。特别地,如果A的第i个字符和B的第j个字符原本就相同,那么我们实际上不需要进行修改操作。在这种情况下,D[i][j]最小可以为D[i-1][j-1]。
dp[i-1][j-1]到dp[i][j]需要进行替换操作,dp[i-1][j]到d[i][j]需要进行删除操作,dp[i][j-1] 到d[i][j]需要进行添加操作。
所以,
当 A[i] == B[j],dp[i][j] = dp[i-1][j-1];
当 A[i] != B[j],dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1
注意,针对第一行,第一列要单独考虑,我们引入 '' 下图所示:
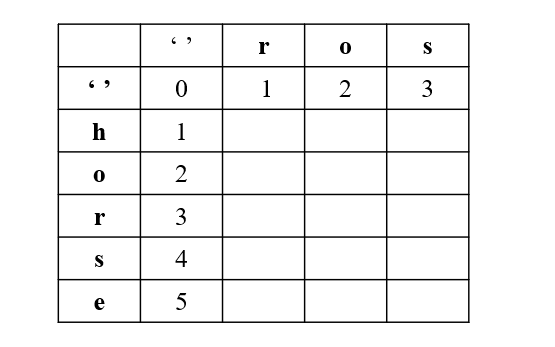
第一行,是 A 为空,变成 B 最少步数,就是插入操作
第一列,是 B 为空,需要的最少步数,就是删除操作
动态规划有两种做法:
- 自底向上的递推法,从起点状态开始扫描,输出值为终点状态值,需要填整个动态规划状态表,尽管不是所有的状态都对终点状态的计算有直接贡献,有些状态其实没有必要计算。递推填表的时间复杂度
O(M*N),空间复杂度可以从O(M*N)优化到O(N)。 - 自顶向下的递归法,从终点状态开始调用递归,扫描所有必需的状态空间,只需要填一部分的动态规划状态表,有些不必要的状态可以直接避免计算。这里的递归法其实是一种深度优先的办法去扫描动态规划的有效状态空间,对于递归过程中的重复计算,可以用记忆化方法剪枝来提高效率。记忆化递归的平均时间时间复杂度
O(M*N),但是时间常数项比递推填表的要小一半,速度更快,极端情况下记忆化递归的时间复杂度可以降为O(N);但是空间复杂度不能优化,为O(M*N)。
自底向上
以word1 = "horse", word2 = "ros"为例:
dp = [[0, 1, 2, 3], ""
[1, 1, 2, 3], h
[2, 2, 1, 2], o
[3, 2, 2, 2], r
[4, 3, 3, 2], s
[5, 4, 4, 3]] e
"" r o s
""是最开始补的一位空字符。
又比如对于word1 = "horse", word2 = "horse"
dp = [[0, 1, 2, 3, 4, 5], ""
[1, 0, 1, 2, 3, 4], h
[2, 1, 0, 1, 2, 3], o
[3, 2, 1, 0, 1, 2], r
[4, 3, 2, 1, 0, 1], s
[5, 4, 3, 2, 1, 0]] e
"" h o r s e
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n1 = len(word1)
n2 = len(word2)
dp = [[0] *(n2+1) for _ in range(n1+1)]
# 第一行
for j in range(1,n2+1):
dp[0][j] = dp[0][j-1] +1
# 第一列
for i in range(1,n1+1):
dp[i][0] = dp[i-1][0] +1
for i in range(1,n1+1):
for j in range(1,n2+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1],dp[i ][j-1],dp[i-1][j ]) +1
return dp[-1][-1]
自顶向下
记忆化递归可以只扫描计算对最后结果有贡献的dp单元值,运算量比递推法要小,速度可以快一倍,极端情况可以将时间复杂度由递推法的O(M*N)降为O(N),但是空间复杂度不能降低。
比如对于word1 = "horse", word2 = "ros"
dp = [[0, 1, -, -], ""
[1, 1, -, -], h
[2, 2, 1, -], o
[3, 2, 2, -], r
[4, 3, 3, 2], s
[5, 4, 4, 3]] e
"" r o s
-的那些状态就可以不用计算了,节省了时间。
又比如word1 = "horse", word2 = "horse"
dp = [[0, -, -, -, -, -], ""
[-, 0, -, -, -, -], h
[-, -, 0, -, -, -], o
[-, -, -, 0, -, -], r
[-, -, -, -, 0, -], s
[-, -, -, -, -, 0]] e
"" h o r s e
对于这个特殊的情况,只需要计算对角线上的那几个状态就可以了。
可以用dp数组做记忆化递归(初始化为-1用来作记录)
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m = len(word1)
n = len(word2)
dp = [[-1]*(n+1) for _ in range(m+1)]
def dp_list(i,j):
if dp[i][j]>=0:# 第一行和第一列初始化已经完成
return dp[i][j] #
if i*j == 0:
dp[i][j] = i+j # 第一行和第一列初始化
elif word1[i-1] == word2[j-1]:
dp[i][j] = dp_list(i - 1, j - 1)
else:
dp[i][j] = min(dp_list(i-1,j),dp_list(i,j-1),dp_list(i-1,j-1))+1
return dp[i][j]
return dp_list(m,n)
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
memo = dict()
def dp(i, j):
if (i, j) in memo:
return memo[(i, j)]
if i * j == 0:
res = i + j
elif word1[i - 1] == word2[j - 1]:
res = dp(i - 1, j - 1)
else:
res = min(dp(i - 1, j), dp(i, j - 1), dp(i - 1, j - 1)) + 1
memo[(i, j)] = res
return res
return dp(len(word1), len(word2))