[数据结构与算法]决策树的构建算法

决策树的构建算法

决策树算法用到的是，纯度的另一面不纯度。

ID3是基本算法，后两种都是在ID3的基础上优化后的算法。

ID3算法

使用信息增益作为不纯度。

即用信息增益来判断当前的节点用什么样的特征来构建决策树。信息增益越大，不确定性的减少程度越大，越适合用来构建决策树。

信息增益

也称作互信息，也就是下图的阴影部分。

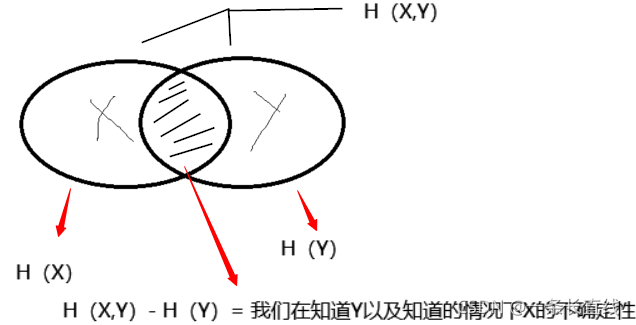
是用来衡量在已知Y的情况下X不确定性的减少程度or在已知X的情况下Y不确定性的减少程度。也就是表示X事件和Y事件的共同信息。

具有对称性。

表示为：$I(X,Y)=H(X)?H(X|Y)$

例子

样本D中有16个样本（统计学），输出0或1。10个输出1，6个输出0。

其中特征A有三种情况

• A1中有4个样本，3个输出1，1个输出0
• A2中有8个样本，5个输出1，3个输出0
• A3中有4个样本，2个输出1，2个输出0

整体的熵：$H(D)=?(\frac{10}{16}?log(\frac{10}{16})+\frac{6}{16}?log(\frac{6}{16})=0.66$

先算整体的熵其实类似于贝叶斯里的先验。之后算在各个特征下整体的不确定性。然后求各个特征的信息增益，比较信息增益，选取最大信息增益所对应的特征。

知道A特征后整体不确定性：$H(D|A)=\frac{4}{16}(?\frac{3}{4}?log\frac{3}{4}?\frac{1}{4}?log\frac{1}{4})+\frac{8}{16}(?\frac{5}{8}?log\frac{5}{8}?\frac{3}{8}?log\frac{3}{8})+\frac{4}{16}(?\frac{2}{4}?log\frac{2}{4}?\frac{2}{4}?log\frac{2}{4})=0.64$

信息增益：$I(D,A)=H(D)?H(D|A)=0.02$

假设还有特征$B、C、F$，对应的信息增益分别为$I(D,B)=0.04、I(D,C)=0.01、I(D,F)=0.1$

所以选取信息增益最大的F特征来做分节点。

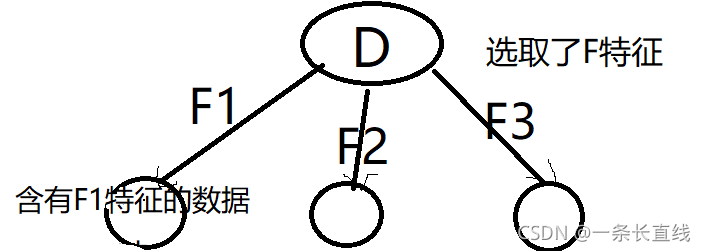
问题

在$D_{F1}$数据集中，特征$F_1$还可以继续用么？

答：如果是离散型特征则不可。已经根据特征F来划分了数据集了，在$D_{F1}$中已经没有特征F了，不可能再有增益了。如果是连续型特征则可以。

另外，用熵选择时候特征不可重复用。用比基尼系数选择时特征可重复用。

构造ID3决策树

1. 选取特征。也就是选择信息增益最大的特征。

2. 阈值的确定：也就是选择判断条件的属性值是什么。选择适当的阈值使得分类错误率最小。注意：阈值设置过高可能会导致欠拟合，过低可能会导致过拟合。

3. 确定停止分裂的情况。

   ? 分支停止条件：

   • 特征已经用完了

   • 剩下的特征整体提供的信息增益小于设定的阈值

   • 新划分出来的数据集里面的样本都一样（如全都是1）?，也就是样本数量为1

   • 最大深度、最小叶子节点数、最小样本分裂数

特性

构建决策树类似于递归。

递归：前进条件+停止条件。

构建决策树的前进条件：增益最大，使规模变小。停止条件如上。

缺点

• 不能处理连续型特征

• 信息增益准则对可取数目较多的属性有所偏好

  ? 比如：在选择特征时，对于$p(X_1)$~$p(X_3)=\frac{1}{2}$和$p(X_1)$~$p(X_6)=\frac{1}{6}$这种情况，ID3决策树更倾向于选择后者。

• 容易过拟合（随机森林可以很大程度上减少过拟合）

• 回归问题

• 因多叉树的结构特点，空间成本大

  由于计算机以二进制存储的特点（0，1），计算机对二叉树会更友好

• 计算涉及到log计算，需要占用较大计算资源

C4.5算法

使用信息增益率作为不纯度。

ID3有【无法处理连续型变量】和【偏向选择子类别多的特征】的缺点就决定了他选择的主观性偏强，并且也存在较大的局限性。于是C4.5就出来解决ID3的缺点。

首先为了解决【无法处理连续型变量】的缺点把连续值变量进行排序成（a1,a2,…an)。再从(a1,a2)区间里取A1作为分界来分裂数据，算信息增益率，从（a2,a3）区间里取A2作为分界来分裂数据，算信息增益率，这样可以得到n-1个信息增益率，然后选最大的。

其次为了解决【偏向选择子类别多的特征】的缺点，C4.5采用了信息增益率进行特征选择，弱化了主观性地偏向子类别多的特征选择。

信息增益率

本质是在信息增益的基础之上乘一个惩罚参数。

公式

信息增益率 = 信息增益 *惩罚参数

信息增益率$:I_R(D,A)=\frac{I(D,A)}{H_A(D)}$

惩罚参数：$\frac{1}{H_A(D)}=\frac{1}{?{\sum }_{i=1}^n\frac{|D_i|}{|D|}lo{g}_2\frac{|D_i|}{|D|}}$

惩罚参数：是数据集D以特征A作为随机变量的熵的倒数，即将特征A取值相同的样本划分到同一个子集中。

• 针对某一特征中类别数量n过多的惩罚。

  特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。

• 针对含有同类别数量的不同特征中各类别频率不等的惩罚。

  例如：现有两个特征A、B，两个特征都包含6各类别。其中特征A中的各类别是均匀的$P(X_1)$~$P(X_6)=\frac{1}{6}$，特征B中的不同类别频率不全相同$P(x_1)=\frac{2}{6}、P(x_2)=\frac{2}{6}、P(x_3)$~$P(X_6)=\frac{1}{12}$。$H_A(D)>H_B(D)$，$A$受到的惩罚更大。也就进一步解决了ID3决策树的倾向缺陷。

$H_A(D)$：对于样本集合$D$，将当前特征A作为随机变量（取值是特征A的各个特征值），求得的经验熵。

例子

样本D中有16个样本（统计学），输出0或1。10个输出1，6个输出0。

其中特征A有三种情况

• A1中有4个样本，3个输出1，1个输出0
• A2中有8个样本，5个输出1，3个输出0
• A3中有4个样本，2个输出1，2个输出0

特征A的熵：$H_A(D)=?(\frac{4}{16}?log\frac{4}{16}+\frac{8}{16}?log\frac{8}{16}+\frac{4}{16}?log\frac{4}{16})=1.03$

缺点

• 回归问题

• 因多叉树的结构特点，空间成本大

  由于计算机以二进制存储的特点（0，1），计算机对二叉树会更友好

• 计算涉及到log计算，需要占用较大计算资源

• 容易过拟合（随机森林可以很大程度上减少过拟合）

• 对连续型变量的处理不够好

  虽然有简单处理（连续性变离散型），但当变量特别大时，处理所需时间过多。

CART算法

使用基尼系数作为不纯度。也就是CART与ID4、C4.5不同的是，CART用基尼指数来判断当前的节点用什么样的特征来构建决策树

CART是一颗二叉树，哪怕某个特征有多类（年龄有青年，中年，老年），也是进行二分叉（青年一个叉，中年老年一个叉）再继续分下去。同时CART也是回归树，同时也是分类树。

基尼指数

表示在样本集合中一个随机选中的样本被分错的概率。

集合的纯度越高（样本集合的凌乱度越低）,也就是说集合中被选中的样本被分错的概率越小，gini指数越小。反之，gini指数越高。

基尼指数（基尼不纯度）= 样本被选中的概率 * 样本被分错的概率

公式

样本集合D中有n各类别，

$gini(D)={\sum }_{k=1}^n{p}_k(1?p_k)=1?{\sum }_{k=1}^n{p}_k^2$

• $p_k$：选中的样本属于k类别的概率，则这个样本被分错的概率是$(1?p_k)$

• ? 一个随机选中的样本可以属于这n个类别中的任意一个，因而对类别加和

• ? 当n=2时，$gini(p)=2p(1?p)$

条件基尼指数：$gini(D,A)={\sum }_{i=1}^k\frac{D_{Ai}}{D}gini(D_{Ai})$

特征选取过程

对于一个具有多个取值（超过2个）的特征，需要计算以每一个取值作为划分点，对样本D划分之后子集的纯度$Gini(D,Ai)$ (其中$Ai$表示特征$A$的可能取值)

然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分，这个划分的划分点，便是使用特征A对样本集合D进行划分的最佳划分点。

分裂中止条件

回归解析用来决定分布是否终止。

理想地说每一个叶节点里都只有一个类别时分类应该停止。

但是很多数据并不容易完全划分，或者完全划分需要很多次分裂，必然造成很长的运行时间，所以CART可以对每个叶节点里的数据分析其均值方差，当方差小于一定值可以终止分裂，以换取计算成本的降低。

优点

• 由于可以使用二叉树的形式分枝，计算机对其会更友好
• 由于去除了对数计算，计算资源得到改善
• 可以结合二叉树的特点，处理连续型特征和做回归

缺点

• 容易过拟合（和ID3一样，存在偏向细小分割）

  解决方法：对特别长的树进行剪枝处理，直接剪掉。

另外：树相关的集成算法如随机森林，GDBT，XGBoost中的弱分类器用的都是CART。