1. 问题描述:?
给两个整数数组?A?和?B?,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1] 。
提示:
1 <= len(A), len(B) <= 1000
0 <= A[i],B[i] < 100
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-length-of-repeated-subarray
2. 思路分析:
分析题目可以知道这道题目类似于最长公共子序列的问题,这里需要求解的是最长公共子数组问题,最长公共子数组问题也是一个经典的问题,比较好的解决是方法是使用二分来解决,我们可以使用二分计算出当前的mid,在nums1中求解出所以长度为mid的子数组,然后在nums2中判断是否存在长度为mid相等的子数组,根据当前长度为mid的check函数的结果来更新l和r,所以问题就转化为如何快速判断两个连续的子序列是否相等,这里可以使用字符串哈希算法快速判断两个连续的子序列是否相等(判断连续的子序列与字符串是否相等的本质上是一样的,字符串累加的是ascii值,序列累加的是对应的数值),字符串哈希使用O(n)的时间来预处理字符串前缀的哈希值,然后就可以使用O(1)的时间查询出任意一个子串的哈希值,字符串哈希涉及到以下几个公式:
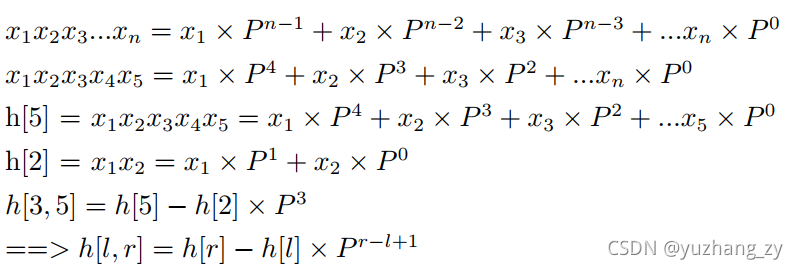
3. 代码如下:
from typing import List
class Solution:
# 查询数组中[l, r]区间的哈希值, 字符串的哈希数组查询的时候是从下标为1开始的
def query(self, h: List[int], l: int, r: int, P: int, p: List[int]):
return h[r] - h[l - 1] * p[r - l + 1]
def check(self, mid: int, ha: List[int], hb: List[int], n: int, m: int, P: int, p: List[int]):
hash = dict()
i = mid
# 将nums1中所有长度为mid的哈希值加入到哈希表中然后再遍历一下nums2中的所有长度为mid的哈希值如果存在两个哈希值是相等的说明满足要求返回True
while i <= n:
hash[self.query(ha, i - mid + 1, i, P, p)] = 1
i += 1
i = mid
# 在nums2中计算所有长度为mid的哈希值并判断是否存在哈希值相等的情况
while i <= m:
t = self.query(hb, i - mid + 1, i, P, p)
if t in hash: return True
i += 1
return False
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
ha, hb = [0], [0]
# p用来计算p的t次幂
p = [1]
# P为经验值, 一般为131,13331这样发生冲突的概率极小可以认为几乎是没有冲突如果发生冲突那么换一个P即可
P = 131
n, m = len(nums1), len(nums2)
# 预处理第一个数组的哈希值
for i in range(n):
ha.append(ha[-1] * P + nums1[i])
p.append(p[-1] * P)
# 预处理第二个数组的哈希值
for i in range(m):
hb.append(hb[-1] * P + nums2[i])
l, r = 0, n
res = 0
while l <= r:
mid = l + r >> 1
# 使用res来记录答案, 长度为mid满足条件说明答案应该是在右边
if self.check(mid, ha, hb, n, m, P, p):
res = mid
l = mid + 1
else:
r = mid - 1
return res