支持向量机SVM详解推导及代码实现smo算法
带约束条件优化问题
再讲SVM算法之前,先了解下带约束条件的优化问题,为后面svm优化奠定基础。
求一个函数的最(极)值
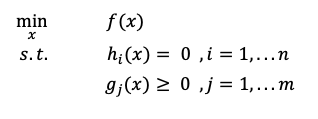
分三种情况:
-
无约束条件: 就是我们最常见的情况,直接对变量求导并令其为零,求极值即可;
-
含有等式约束:引入拉格朗日乘子,拉格朗日乘子的思想是将约束条件函数与原函数联系到一起,构造拉格朗日函数L,求导等于0即为最优解; L ( x , λ ) = f ( x ) ? ∑ i = 1 n λ i h i ( x ) L(x,\lambda)=f(x)-\sum_{i=1}^{n}\lambda_ih_i(x) L(x,λ)=f(x)?∑i=1n?λi?hi?(x)
-
不等式约束 :在等式约束条件的基础上,再引入一个松弛变量β,也叫KKT乘子。
L ( x , λ , β ) = f ( x ) ? ∑ i = 1 n λ i h i ( x ) ? ∑ i = 1 n β i g i ( x ) L(x,\lambda,\beta)=f(x)-\sum_{i=1}^{n}\lambda_ih_i(x)-\sum_{i=1}^{n}\beta_ig_i(x) L(x,λ,β)=f(x)?∑i=1n?λi?hi?(x)?∑i=1n?βi?gi?(x)
SVM支持向量机原理
SVM最开始提出是用来解决二分类问题的,但后来可以应用到多分类,但基础还是多分类。比如,一共有5类,先把1作为1类,把2345作为一类,不属于1分类里面的数据,就在2345里面找,再把2345再分为两类,2和345两类,一直向这样迭代…
最大间隔分类器
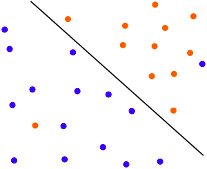
SVM的核心思想:我们要找到一个超平面(w,b),使得离超平面最近的样本点距离最大。
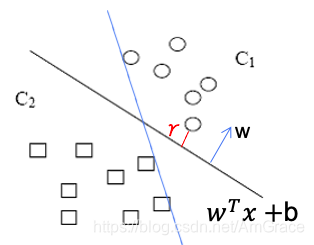
如上图,我们有这样两类数据,我们的任务就是要找到这样一条线,把这两类数据分开。
我们以线性分类器为例,我们可以用1表示属于类别C1,-1类别C2,找到一个超平面,使两类数据分开,这个超平面的函数方程是:
𝑤
𝑇
𝑥
+
𝑏
=
0
𝑤^𝑇 𝑥+𝑏=0
wTx+b=0
可以想象得到,将+1和-1分开的这条线,其实是有很多条的,哪一条最合适呢?比如图上有两个超平面,当然是黑色的合适些,因为蓝色超平面里样本点很近,就很容易分类错误,所以他的泛化误差没有另外一个好。
因此,SVM的核心是:我们要找到一个超平面(w,b),使得离超平面最近的样本点距离最大。
我们的最大间隔分类就是使这个点到直线的距离γ(又称为间隔margin)最大,并且在正确分类(因为这个是一个分类器)情况下,
𝑤
𝑇
𝑥
+
𝑏
<
0
,
y
=
?
1
,
𝑤
𝑇
𝑥
+
𝑏
>
0
,
y
=
+
1
𝑤^𝑇 𝑥+𝑏<0,y=-1, 𝑤^𝑇 𝑥+𝑏>0,y=+1
wTx+b<0,y=?1,wTx+b>0,y=+1,整合这两个情况,记为
y
(
𝑤
𝑇
𝑥
+
𝑏
)
>
0
y(𝑤^𝑇 𝑥+𝑏)>0
y(wTx+b)>0。因此,我们的优化目标变为:
m
a
x
????
γ
s
.
t
??
y
i
(
w
T
x
i
+
b
)
>
0
max \ \ \ \ \gamma\\s.t \ \ y_i(w^Tx_i+b)>0
max????γs.t??yi?(wTxi?+b)>0
又因为点到直线的距离公式:
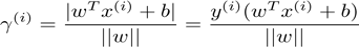
(第二个等式是因为去绝对值,前面讲过约束条件大于0了)
有n个样本点,就有n个距离,我们要找离超平面最近的,因此, γ = m i n γ ( i ) \gamma=min\gamma^{(i)} γ=minγ(i)
(接下来都是对优化函数的化简,因为其他人讲SVM都是一笔带过,直接把它化成了最后的结果,省去了很多步骤,这里我详细讲一下是如何化简的)
把两个式子带入优化目标中,整理一下得:
m
a
x
w
,
b
?
m
x
(
i
)
i
n
1
∣
∣
w
∣
∣
y
(
i
)
(
w
T
x
(
i
)
+
b
)
\underset{w,b}{max} \ \underset{x^{(i)}}min\frac{1}{||w||y^{(i)}}(w^Tx^{(i)}+b)
w,bmax??x(i)m?in∣∣w∣∣y(i)1?(wTx(i)+b)
s
.
t
.
???
y
i
(
w
T
+
b
)
>
0
s.t. \ \ \ y^i(w^T+b)>0
s.t.???yi(wT+b)>0
上述优化目标也再次说明,SVM的核心思想,求离超平面最近的点的距离最大!
公式中||w||可以提到前面(因为min中和w无关),因此优化目标变为:
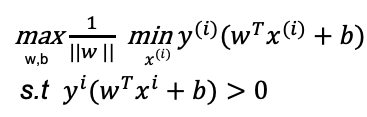
还可以化简…看下面的约束条件𝑦^𝑖 (𝑤^𝑇 𝑥^𝑖+𝑏)>0,所以一定存在?𝛾>0,使得𝑚𝑖𝑛 𝑦^𝑖 (𝑤^𝑇 𝑥^𝑖+𝑏)=𝛾 (因为它的最小值等于𝛾且大于零,所以𝑦^𝑖 (𝑤^𝑇 𝑥^𝑖+𝑏)所有的值都大于0) 。𝑚𝑖𝑛 𝑦^𝑖 (𝑤^𝑇 𝑥^𝑖+𝑏)=𝛾 这个形式带入上面的函数中,整理得:
m
w
,
b
a
x
1
∣
∣
w
∣
∣
γ
\underset{w,b}max\frac{1}{||w||}\gamma
w,bm?ax∣∣w∣∣1?γ
s
.
t
.
?
y
i
(
w
T
x
i
+
b
)
>
0
s.t. \ y_i(w^Tx_i+b)>0
s.t.?yi?(wTxi?+b)>0
还是看
m
i
n
?
y
i
(
w
T
x
i
+
b
)
=
γ
min \ y^i(w^Tx^i+b)=\gamma
min?yi(wTxi+b)=γ,可以推出
𝑦
𝑖
(
𝑤
𝑇
𝑥
𝑖
+
𝑏
)
≥
γ
𝑦^𝑖 (𝑤^𝑇 𝑥^𝑖+𝑏)\ge\gamma
yi(wTxi+b)≥γ(最小值等于𝛾,所以它的所有值都大于等于𝛾),因此我们的约束条件变为:
m
w
,
b
a
x
1
∣
∣
w
∣
∣
γ
s
.
t
.
?
y
i
(
w
T
x
i
+
b
)
≥
γ
\underset{w,b}max\frac{1}{||w||}\gamma \\ s.t. \ y_i(w^Tx_i+b)\ge\gamma
w,bm?ax∣∣w∣∣1?γs.t.?yi?(wTxi?+b)≥γ
(接下来要讲的是比较重要的,为什么𝛾=1,很多书都没写)
因为我们的超平面方程为
𝑤
𝑇
𝑥
+
𝑏
=
0
𝑤^𝑇 𝑥+𝑏=0
wTx+b=0 ,同比例放大缩小w和b,我们的超平面不变,为什么?因为等式两边都乘以2之后:
2
𝑤
𝑇
𝑥
+
2
𝑏
=
2
?
0
2𝑤^𝑇 𝑥+2𝑏=2*0
2wTx+2b=2?0, 这个等式没变,所以超平面也没变。
我是这样理解的,我觉得这种理解方法更容易理解,举个例子:比如在三维空间内,我们同比例缩放w和b,就相当于把我们的超平面的面积增大或者缩小,但其实它的所在位置没有变化,因此这个超平面没有变化!
所以我们将𝛾除以一个适当的值,我们的𝛾是可以等于1的,因此,最后化简为:
m
w
,
b
a
x
1
∣
∣
w
∣
∣
\underset{w,b} max\frac{1}{||w||}
w,bm?ax∣∣w∣∣1?
s
.
t
.
?
y
i
(
w
T
x
i
+
b
)
≥
1
s.t. \ y_i(w^Tx_i+b)\ge1
s.t.?yi?(wTxi?+b)≥1
再化简:
m
w
,
b
i
n
?
1
2
∣
∣
w
∣
∣
2
\underset{w,b} min \ \frac{1}{2}||w||^2
w,bm?in?21?∣∣w∣∣2
s
.
t
.
?
y
i
(
w
T
x
i
+
b
)
≥
1
s.t. \ y_i(w^Tx_i+b)\ge1
s.t.?yi?(wTxi?+b)≥1
(这的二分之一和平方是因为后面要优化这个函数,对他求导,使计算更加简便,并且对我们找这个超平面无影响)
所以问题就变成了一个带约束条件的优化问题,前面提到过,引入拉格朗日乘子,构造拉格朗日函数L,求它的最大值:
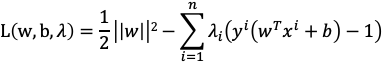
因此,优化目标函数变为
m
w
,
b
i
n
?
m
λ
a
x
?
L
(
w
,
b
,
λ
)
\underset{w,b}min \ \underset{\lambda}max \ L(w,b,\lambda)
w,bm?in?λm?ax?L(w,b,λ)
为什么可以这样化简呢?可以这样理解,以下不是证明,只是逻辑上的理解:
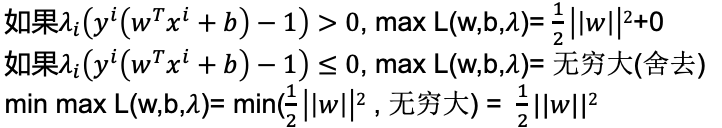
再经过强对偶化简为:
m
λ
a
x
?
m
w
,
b
i
n
?
L
(
w
,
b
,
λ
)
\underset{\lambda}max \ \underset{w,b}min \ L(w,b,\lambda)
λm?ax?w,bm?in?L(w,b,λ)
强对偶是可以进行证明的,但是这个特别复杂,有兴趣的可以单独了解。为什么要这样化简,因为优化拉格朗日函数L,是一个凸优化问题,求它的最大值不方便,求最小值方便,所以要用强对偶。因此, m w , b i n ? L ( w , b , λ ) \underset{w,b}min \ L(w,b,\lambda) w,bm?in?L(w,b,λ)对w和b求偏导令其为0, w ? = ∑ i = 1 n λ i y i x i , ∑ i = 1 n λ i y i = 0 w^*=\sum_{i=1}^{n}\lambda_iy_ix_i,\sum_{i=1}^{n}\lambda_iy_i=0 w?=∑i=1n?λi?yi?xi?,∑i=1n?λi?yi?=0
把w带入拉格朗日函数L中,化简整理得:
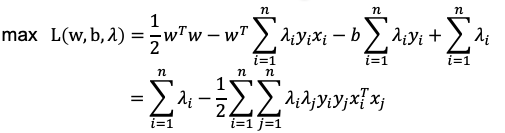
和前面一样,凸优化问题,求最大值比较困难,我们取相反数求最小值,最终将问题转化为:
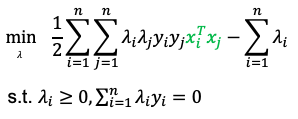
为什么要用对偶问题
- 首先是我们有不等式约束方程,这就需要我们写成min max的形式来得到最优解。而这种写成这种形式对w,b不能求导,所以我们需要转换成max min的形式。而为了满足这种对偶变换成立,就需要满足KKT条件(KKT条件是原问题与对偶问题等价的必要条件,当原问题是凸优化问题时,变为充要条件);
- 对偶问题将原始问题中的不等式约束条件转为了对偶问题中的等式约束条件,方便引入拉格朗日函数;
- 方便核函数的引入kernel。
核函数kernel function
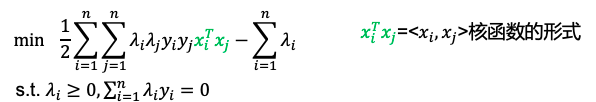
核函数
K
(
x
,
z
)
=
?
(
𝑥
)
T
?
(
𝑧
)
=
<
?
(
𝑥
)
,
?
(
𝑧
)
>
=
(
x
T
z
)
2
K(x,z)=\text{\o}(𝑥)^T\text{\o}(𝑧)=<\text{\o}(𝑥),\text{\o}(𝑧)> =(x^Tz)^2
K(x,z)=?(x)T?(z)=<?(x),?(z)>=(xTz)2, 𝜙是从n维到m维映射。举个例子:
x
=
(
x
1
x
2
x
3
)
3
维
,
z
=
(
z
1
z
2
z
3
)
3
维
,
?
(
𝑥
)
=
(
x
1
x
1
x
1
x
2
x
1
x
3
x
2
x
1
x
2
x
2
x
2
x
3
x
3
x
1
x
3
x
2
x
3
x
3
)
9
维
,
?
(
z
)
=
(
z
1
z
1
z
1
z
2
z
1
z
3
z
2
z
1
z
2
z
2
z
2
z
3
z
3
z
1
z
3
z
2
z
3
z
3
)
9
维
,
K
(
x
,
z
)
=
(
x
T
,
z
)
2
x=\underset{3维}{\begin{pmatrix}x_1 \\ x_2 \\ x_3\end{pmatrix}},z=\underset{3维}{\begin{pmatrix}z_1 \\ z_2 \\ z_3\end{pmatrix}},\text{\o}(𝑥)=\underset{9维}{\begin{pmatrix}x_1x_1 \\ x_1x_2 \\ x_1x_3 \\ x_2x_1 \\ x_2x_2 \\ x_2x_3 \\ x_3x_1 \\ x_3x_2 \\ x_3x_3\end{pmatrix}},\text{\o}(z)=\underset{9维}{\begin{pmatrix}z_1z_1 \\ z_1z_2 \\ z_1z_3 \\ z_2z_1 \\ z_2z_2 \\ z_2z_3 \\ z_3z_1 \\ z_3z_2 \\ z_3z_3\end{pmatrix}},K(x,z)=(x^T,z)^2
x=3维???x1?x2?x3??????,z=3维???z1?z2?z3??????,?(x)=9维???????????????x1?x1?x1?x2?x1?x3?x2?x1?x2?x2?x2?x3?x3?x1?x3?x2?x3?x3??????????????????,?(z)=9维???????????????z1?z1?z1?z2?z1?z3?z2?z1?z2?z2?z2?z3?z3?z1?z3?z2?z3?z3??????????????????,K(x,z)=(xT,z)2
Kernel函数将原本9维的计算变成了求x和z内积的平方,变成3维的问题。因此kernel函数就是帮我们省去了在高位空间里进行繁琐计算的简便运算法.
为什么要用核函数?
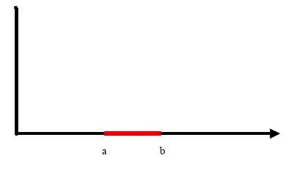
举个例子:假设把a和b之间红色部分里的所有点定为正类,两边的黑色部分里的点定为负类。试问能找到一个线性函数把两类正确分开吗?
答案是不能的,因为二维空间里的线性函数就是指直线,显然找不到符合条件的直线。但我们可以找到一条二次曲线将它们分开,如下图。
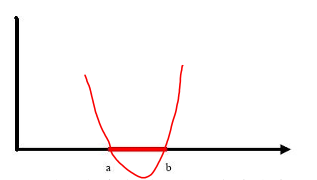
因此,这个二次曲线的函数表达式
g
(
x
)
=
c
0
+
c
1
x
+
c
2
x
2
=
<
a
,
y
>
g(x)=c_0+c_1x+c_2x^2=<a,y>
g(x)=c0?+c1?x+c2?x2=<a,y>,新建两个向量:
a = ( a 1 a 2 a 3 ) = ( c 0 c 1 c 2 ) , y = ( y 1 y 2 y 3 ) = ( 1 2 x 2 ) a=\begin{pmatrix}a_1 \\ a_2 \\ a_3\end{pmatrix}=\begin{pmatrix}c_0 \\ c_1 \\ c_2\end{pmatrix},y=\begin{pmatrix}y_1 \\ y_2 \\ y_3\end{pmatrix}=\begin{pmatrix}1 \\ 2 \\ x^2\end{pmatrix} a=???a1?a2?a3?????=???c0?c1?c2?????,y=???y1?y2?y3?????=???12x2????
所以,原来在二维空间中一个线性不可分的问题,映射到高维空间后,变成了线性可分的。
看下图,左边的数据本来是线性不可分的,经过了
?
\text{\o}
?函数后,有一个超平面可以将原本线性不可分的数据变成了线性可分的。
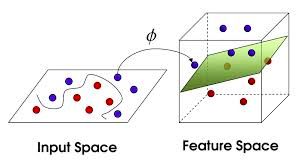
软间隔支持向量机 (soft margin)
我们之前讲是hard margin,引入soft的原因是因为:在hard margin的时候是认为这个数据是最理想的情况下是线性可分的,但是实际情况是比较复杂的,要么数据是不可分的,或者这个数据是可分的但是这个数据是存在噪声的。
在这种情况下,我们可以把噪声点剔除,可以利用软间隔支持向量机,通俗的来说就是可以容错,如下图:
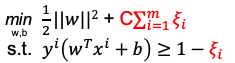
软误差:
∑
i
=
1
m
ξ
i
\sum_{i=1}^{m}\xi_i
∑i=1m?ξi? ,所有数据元组松弛变量的和,C>0为惩罚参数, C的取值用来在数据拟合之间找到平衡。C越大,对目标函数的损失也越大,此时就暗示着你非常不愿意放弃这些离群点。
SVM涉及到的内容基本都讲到了,但是这里面还是很多细节,有兴趣的大家可以单独去了解,去学习。接下来讲一下SVM代码实现,最简答的算法smo算法。
SMO算法实现
SMO算法思路
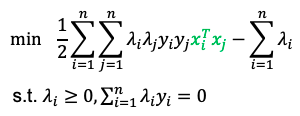
其中
λ
=
[
λ
1
,
λ
2
,
λ
3
,
λ
4
…
…
λ
n
]
\lambda=[\lambda_1, \lambda_2, \lambda_3,\lambda_4……\lambda_n]
λ=[λ1?,λ2?,λ3?,λ4?……λn?]
smo算法思路:选取两个优化变量 λ i , λ j \lambda_i, \lambda_j λi?,λj? ,把剩余变量看做是固定的常数,进行优化目标函数,再迭代 λ i , λ j \lambda_i, \lambda_j λi?,λj?,再优化,直到所有的 λ \lambda λ被优化完,迭代终止。
为什么要选取两个变量进行优化,因为有限制条件 ∑ i = 1 n λ i y i = 0 \sum_{i=1}^{n}\lambda_iy_i=0 ∑i=1n?λi?yi?=0,只优化一个的话,会不满足这个约束,所以我们选择两个,其中一个变化,另外一个也随着变化,然后把剩下的变量看成一个常数。
为了方便讲解,先举一对变量 λ 1 , λ 2 \lambda_1, \lambda_2 λ1?,λ2?优化,令 K i j = x i T x j K_{ij}=x_i^Tx_j Kij?=xiT?xj?,把含有 λ 1 , λ 2 \lambda_1, \lambda_2 λ1?,λ2?变量的写出来,剩下的变量看做成常数用R表示:
f ( λ 1 , λ 2 ) = 1 2 λ 1 2 𝐾 11 + 1 2 λ 2 2 𝐾 22 + λ 1 λ 2 y 1 y 2 K 12 + y 1 λ 1 ∑ i = 3 n y i λ i K i 1 + y 2 λ 2 ∑ i = 3 n y i λ i K i 2 ? λ 1 ? λ 2 + R f(\lambda_1, \lambda_2)=\frac{1}{2} \lambda_1^2𝐾_{11}+\frac{1}{2} \lambda_2^2𝐾_{22}+ \lambda_1\lambda_2y_1y_2K_{12}+y_1\lambda_1\sum_{i=3}^{n}y_i\lambda_iK_{i1}+y_2\lambda_2\sum_{i=3}^{n}y_i\lambda_iK_{i2}-\lambda_1-\lambda_2+R f(λ1?,λ2?)=21?λ12?K11?+21?λ22?K22?+λ1?λ2?y1?y2?K12?+y1?λ1?∑i=3n?yi?λi?Ki1?+y2?λ2?∑i=3n?yi?λi?Ki2??λ1??λ2?+R
于是就是一个二元函数优化:
a
r
g
??
m
a
x
λ
1
,
λ
2
f
(
λ
1
,
λ
2
)
arg \ \ max_{\lambda_1, \lambda_2}f(\lambda_1, \lambda_2)
arg??maxλ1?,λ2??f(λ1?,λ2?)
约束条件同样写成:
λ 1 y 1 + λ 2 y 2 + ∑ i = 3 n λ i y i = 0 \lambda_1y_1+\lambda_2y_2+\sum_{i=3}^{n}\lambda_iy_i=0 λ1?y1?+λ2?y2?+∑i=3n?λi?yi?=0,将 ∑ i = 3 n λ i y i \sum_{i=3}^{n}\lambda_iy_i ∑i=3n?λi?yi?看成常数C
所以可以写成: λ 1 y 1 + λ 2 y 2 = ? ∑ i = 3 n λ i y i = C \lambda_1y_1+\lambda_2y_2=-\sum_{i=3}^{n}\lambda_iy_i=C λ1?y1?+λ2?y2?=?∑i=3n?λi?yi?=C,等式两边同时乘以 y 1 y_1 y1?
因为 y i = ± 1 y_i=±1 yi?=±1,所以 y 1 2 = 1 y_1^2=1 y12?=1,因此 λ 1 = y 1 ( C ? λ 2 y 2 ) \lambda_1=y_1(C-\lambda_2y_2) λ1?=y1?(C?λ2?y2?),带入优化函数f中,就只有含有一个变量 λ 2 \lambda_2 λ2?,直接优化即可,令 v 1 = ∑ i = 3 N λ i y i K i , 1 , v 2 = ∑ i = 3 N λ i y i K i , 2 v_1=\sum_{i=3}^{N}\lambda_iy_iK_{i,1},v_2=\sum_{i=3}^{N}\lambda_iy_iK_{i,2} v1?=∑i=3N?λi?yi?Ki,1?,v2?=∑i=3N?λi?yi?Ki,2?:
f
(
λ
2
)
=
1
2
λ
1
2
𝐾
11
+
1
2
λ
2
2
𝐾
22
+
λ
1
λ
2
y
1
y
2
K
12
+
y
1
λ
1
v
1
+
y
2
λ
2
v
2
?
λ
1
?
λ
2
+
C
f( \lambda_2)=\frac{1}{2} \lambda_1^2𝐾_{11}+\frac{1}{2} \lambda_2^2𝐾_{22}+ \lambda_1\lambda_2y_1y_2K_{12}+y_1\lambda_1v_1+y_2\lambda_2v_2-\lambda_1-\lambda_2+C
f(λ2?)=21?λ12?K11?+21?λ22?K22?+λ1?λ2?y1?y2?K12?+y1?λ1?v1?+y2?λ2?v2??λ1??λ2?+C
对f函数求导得:
?
f
(
λ
2
)
?
λ
2
=
?
(
K
11
+
K
22
?
2
K
12
)
λ
2
+
K
11
C
y
2
?
K
12
C
y
2
+
v
1
y
2
?
v
2
y
2
?
y
1
y
2
+
y
2
2
=
0
\frac{\partial f(\lambda_2)}{\partial \lambda_2}=-(K_{11}+K_{22}-2K_{12})\lambda_2+K_{11}Cy_2-K_{12}Cy_2+v_1y_2-v_2y_2-y_1y_2+y_2^2=0
?λ2??f(λ2?)?=?(K11?+K22??2K12?)λ2?+K11?Cy2??K12?Cy2?+v1?y2??v2?y2??y1?y2?+y22?=0
下面我们稍微对上式进行下变形,因为参数
λ
\lambda
λ是不断更新迭代的,所以会有更新前
λ
o
l
d
\lambda_{old}
λold?更新后
λ
n
e
w
\lambda_{new}
λnew?的值。
因为SVM对数据点的预测值为:
f
(
x
)
=
w
T
x
i
+
b
=
∑
i
=
1
N
λ
i
y
i
K
(
x
i
,
x
)
+
b
f(x)=w^Tx_i+b=\sum_{i=1}^{N}\lambda_iy_iK(x_i,x)+b
f(x)=wTxi?+b=∑i=1N?λi?yi?K(xi?,x)+b
则用
v
1
,
v
2
v_1,v_2
v1?,v2?表示成:
v 1 = ∑ i = 3 N λ i y i K 1 i = f ( x 1 ) ? λ 1 y 1 K 11 ? λ 2 y 2 K 12 ? b v_1=\sum_{i=3}^{N}\lambda_iy_iK_{1i}=f(x_1)-\lambda_1y_1K_{11}-\lambda_2y_2K_{12}-b v1?=∑i=3N?λi?yi?K1i?=f(x1?)?λ1?y1?K11??λ2?y2?K12??b
v 2 = ∑ i = 3 N λ i y i K 2 i = f ( x 2 ) ? λ 1 y 1 K 12 ? λ 2 y 2 K 22 ? b v_2=\sum_{i=3}^{N}\lambda_iy_iK_{2i}=f(x_2)-\lambda_1y_1K_{12}-\lambda_2y_2K_{22}-b v2?=∑i=3N?λi?yi?K2i?=f(x2?)?λ1?y1?K12??λ2?y2?K22??b
已知 λ 1 = y 2 ( C ? λ 2 y 2 ) \lambda_1=y_2(C-\lambda_2y_2) λ1?=y2?(C?λ2?y2?),可得到:
v 1 ? v 2 = f ( x 1 ) ? f ( x 2 ) ? K 11 C + k 12 C + ( K 11 + K 22 ? 2 K 12 ) λ 2 y 2 v_1-v_2=f(x_1)-f(x_2)-K_{11}C+k_{12}C+(K_{11}+K_{22}-2K_{12})\lambda_2y_2 v1??v2?=f(x1?)?f(x2?)?K11?C+k12?C+(K11?+K22??2K12?)λ2?y2?
将 v 1 ? v 2 v_1-v_2 v1??v2?带入表达式 ? f ( λ 2 ) ? λ 2 \frac{\partial f(\lambda_2)}{\partial \lambda_2} ?λ2??f(λ2?)?得到:
? f ( λ 2 ) ? λ 2 = ? ( K 11 + K 22 ? 2 K 12 ) λ 2 n e w + ( K 11 + K 22 ? 2 K 12 ) λ 2 o l d + y 2 [ y 2 ? y 1 + f ( x 1 ) ? f ( x 2 ) ] \frac{\partial f(\lambda_2)}{\partial \lambda_2}=-(K_{11}+K_{22}-2K_{12})\lambda_2^{new}+(K_{11}+K_{22}-2K_{12})\lambda_2^{old}+y_2[y_2-y_1+f(x_1)-f(x_2)] ?λ2??f(λ2?)?=?(K11?+K22??2K12?)λ2new?+(K11?+K22??2K12?)λ2old?+y2?[y2??y1?+f(x1?)?f(x2?)]
我们记
E
i
E_i
Ei?为svm预测值与真实值的误差:
E
i
=
f
(
x
i
)
?
y
i
E_i=f(x_i)-y_i
Ei?=f(xi?)?yi?
令
η
=
K
11
+
K
22
?
2
K
12
\eta=K_{11}+K_{22}-2K_{12}
η=K11?+K22??2K12?
? f ( λ 2 ) ? λ 2 = ? η λ 2 n e w + η λ 2 o l d + y 2 ( E 1 ? E 2 ) = 0 \frac{\partial f(\lambda_2)}{\partial \lambda_2}=- \eta\lambda_2^{new}+\eta\lambda_2^{old}+y_2(E_1-E_2)=0 ?λ2??f(λ2?)?=?ηλ2new?+ηλ2old?+y2?(E1??E2?)=0,得到:
λ 2 n e w = λ 2 o l d + y 2 ( E 1 ? E 2 ) η \lambda_2^{new}=\lambda_2^{old}+\frac{y_2(E_1-E_2)}{\eta} λ2new?=λ2old?+ηy2?(E1??E2?)?
这样我们就可以通过不断迭代更新参数进行优化了。
以上是没有讨论了带约束条件的,但是在SVM中是有约束条件的,即:
λ
1
y
1
+
λ
2
y
2
=
?
∑
i
=
3
n
λ
i
y
i
=
γ
\lambda_1y_1+\lambda_2y_2=-\sum_{i=3}^{n}\lambda_iy_i=\gamma
λ1?y1?+λ2?y2?=?∑i=3n?λi?yi?=γ
0
≤
λ
i
≤
C
0≤\lambda_i≤C
0≤λi?≤C
因为 y i = ± 1 y_i=±1 yi?=±1,所以还要分情况讨论, y i = 1 y_i=1 yi?=1或者-1。以y1 y2 为例, λ 1 = y 1 ( γ ? λ 2 y 2 ) = y 1 γ ? λ 2 y 1 y 2 \lambda_1=y_1(\gamma-\lambda_2y_2)=y_1\gamma-\lambda_2y_1y_2 λ1?=y1?(γ?λ2?y2?)=y1?γ?λ2?y1?y2?
分情况讨论
第一种情况:当
y
1
和
y
2
y_1和y_2
y1?和y2?异号时,
λ
1
=
y
1
C
+
λ
2
\lambda_1=y_1C+\lambda_2
λ1?=y1?C+λ2?,这里面又分为两种情况,当y1等于1或者-1时,因此有:
(
1
)
λ
1
=
C
+
λ
2
(1)\lambda_1=C+\lambda_2
(1)λ1?=C+λ2? 和
(
2
)
λ
1
=
?
C
+
λ
2
(2)\lambda_1=-C+\lambda_2
(2)λ1?=?C+λ2?,这就变成了一个线性规划问题,把图画出来:
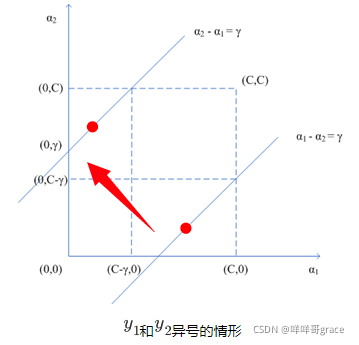
λ
1
和
λ
2
\lambda_1和\lambda_2
λ1?和λ2?既要在矩形方框内,又要在直线上,因此可以写为:
下界:
L
=
m
a
x
(
0
,
λ
2
o
l
d
?
λ
1
o
l
d
)
L=max(0,\lambda_2^{old}-\lambda_1^{old})
L=max(0,λ2old??λ1old?)
上界:
H
=
m
i
n
(
C
,
C
+
λ
2
o
l
d
?
λ
1
o
l
d
)
H=min(C,C+\lambda_2^{old}-\lambda_1^{old})
H=min(C,C+λ2old??λ1old?)
第二种情况:当
y
1
和
y
2
y_1和y_2
y1?和y2?同号时,同理,上下界:
下界:
L
=
m
a
x
(
0
,
λ
2
+
λ
1
?
C
)
L=max(0,\lambda_2+\lambda_1-C)
L=max(0,λ2?+λ1??C)
上界:
H
=
m
i
n
(
C
,
λ
2
+
λ
1
)
H=min(C,\lambda_2+\lambda_1)
H=min(C,λ2?+λ1?)
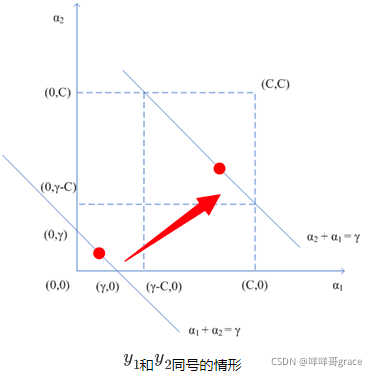
根据
λ
1
o
l
d
y
1
+
λ
2
o
l
d
y
2
=
λ
1
n
e
w
y
1
+
λ
2
n
e
w
y
2
\lambda_1^{old}y_1+\lambda_2^{old}y_2=\lambda_1^{new}y_1+\lambda_2^{new}y_2
λ1old?y1?+λ2old?y2?=λ1new?y1?+λ2new?y2?得到
λ 1 n e w = λ 1 o l d + y 1 y 2 ( λ 2 o l d ? λ 2 n e w ) \lambda_1^{new}=\lambda_1^{old}+y_1y_2(\lambda_2^{old}-\lambda_2^{new}) λ1new?=λ1old?+y1?y2?(λ2old??λ2new?)
这样,我们的一对 λ i , λ j \lambda_i,\lambda_j λi?,λj?就能优化更新了。
b阈值更新
更新了一对 λ i , λ j \lambda_i,\lambda_j λi?,λj?之后我们要计算b,因为有 f ( x ) = w T x i + b = ∑ i = 1 N λ i y i K ( x i , x ) + b f(x)=w^Tx_i+b=\sum_{i=1}^{N}\lambda_iy_iK(x_i,x)+b f(x)=wTxi?+b=∑i=1N?λi?yi?K(xi?,x)+b
且优化样本都满足kkt条件
当 λ 1 n e w \lambda_1^{new} λ1new?不在边界上,即在 0 < λ 1 n e w < C 0<\lambda_1^{new}<C 0<λ1new?<C,根据kkt条件相应的数据点为支持向量(支持向量就是离超平面最近的那个点),满足 y 1 ( w T x + b ) = 1 y_1(w^Tx+b)=1 y1?(wTx+b)=1,两边同乘以y1得 ∑ i = 1 N λ i y i K i 1 + b = y 1 \sum_{i=1}^{N}\lambda_iy_iK_{i1}+b=y_1 ∑i=1N?λi?yi?Ki1?+b=y1?,因此得到
b 1 n e w = y 1 ? ∑ i = 3 N λ i y i K i 1 ? λ 1 n e w y 1 K 11 ? λ 2 n e w y 2 K 21 b_1^{new}=y_1-\sum_{i=3}^{N}\lambda_iy_iK_{i1}-\lambda_1^{new}y_1K_{11}-\lambda_2^{new}y_2K_{21} b1new?=y1??∑i=3N?λi?yi?Ki1??λ1new?y1?K11??λ2new?y2?K21?
根据 ∑ i = 1 N λ i y i K i 1 + b = y 1 \sum_{i=1}^{N}\lambda_iy_iK_{i1}+b=y_1 ∑i=1N?λi?yi?Ki1?+b=y1?,前b中的两项等于:
y 1 ? ∑ i = 3 N λ i y i K i 1 = ? E 1 + λ 1 o l d y 1 K 11 + λ 2 o l d y 2 K 21 + b o l d y_1-\sum_{i=3}^{N}\lambda_iy_iK_{i1}=-E_1+\lambda_1^{old}y_1K_{11}+\lambda_2^{old}y_2K_{21}+b^{old} y1??∑i=3N?λi?yi?Ki1?=?E1?+λ1old?y1?K11?+λ2old?y2?K21?+bold
当 0 < λ 2 n e w < C 0<\lambda_2^{new}<C 0<λ2new?<C,可以得到:
b 2 n e w = ? E 2 ? y 1 K 12 ( λ 1 n e w ? λ 1 o l d ) ? y 2 K 22 ( λ 2 n e w ? λ 2 o l d ) + b o l d b_2^{new}=-E_2-y_1K_{12}(\lambda_1^{new}-\lambda_1^{old})-y_2K_{22}(\lambda_2^{new}-\lambda_2^{old})+b^{old} b2new?=?E2??y1?K12?(λ1new??λ1old?)?y2?K22?(λ2new??λ2old?)+bold
当b1和b2都有效的时候既是他们相等的时候,即 b n e w = b 1 n e w = b 2 n e w b^{new}=b_1^{new}=b_2^{new} bnew=b1new?=b2new?
当 λ 1 , λ 2 \lambda_1,\lambda_2 λ1?,λ2?都在边界上时,SMO选择他们的重点作为新的值:
b n e w = b 1 n e w + b 2 n e w 2 b^{new}=\frac{b_1^{new}+b_2^{new}}{2} bnew=2b1new?+b2new??
SMO代码实现
首先定义辅助函数,后面会用到
# 辅助函数
# 修剪alpha的值 L和H之间
def clip(alpha, L, H):
if alpha < L:
return L
if alpha > H:
return H
else:
return alpha
# 在0到m中随机选择除了i以外剩余的数
def select_j(i, m):
l = list(range(m)) # 0-m
seq = l[:i] + l[i+1:]
return random.choice(seq)
# 通过已知数据点和拉格朗日乘子获得分割超平面参数w
def get_w(alphas, dataset, labels):
alphas, dataset, labels = np.array(alphas), np.array(dataset), np.array(labels)
yx = labels.reshape(1,-1).T*np.array([1,1])*dataset # reshape(1,-1)变成一行
w = np.dot(yx.T, alphas)
return w.tolist()
# smo代码
def simple_smo(dataset, labels, C, max_iter):
# 初始化参数
dataset = np.array(dataset)
m, n = dataset.shape
labels = np.array(labels)
alphas = np.zeros(m)
b = 0
it = 0
def f(x):
"SVM分类器函数 y = w^Tx + b"
# Kernel function vector.
x = np.matrix(x).T
data = np.matrix(dataset)
ks = data*x
# Predictive value.
wx = np.matrix(alphas*labels)*ks
fx = wx + b
return fx[0, 0]
# 迭代开始,选一对ai和aj进行迭代
while it < max_iter:
pair_changed = 0 # 迭代一次计数一次
for i in range(m):
a_i, x_i, y_i = alphas[i], dataset[i], labels[i]
fx_i = f(x_i) # 分类器函数y=wTx+b
E_i = fx_i - y_i # 预测值和真实值误差
j = select_j(i, m)
a_j, x_j, y_j = alphas[j], dataset[j], labels[j]
fx_j = f(x_j)
E_j = fx_j - y_j
K_ii, K_jj, K_ij = np.dot(x_i, x_i), np.dot(x_j, x_j), np.dot(x_i, x_j)
eta = K_ii + K_jj - 2*K_ij
if eta <= 0:
print('WARNING eta <= 0')
continue #跳出此次循环
# 获取更新的alpha对
a_i_old, a_j_old = a_i, a_j
a_j_new = a_j_old + y_j*(E_i - E_j)/eta
# 对alpha进行修剪
if y_i != y_j:
L = max(0, a_j_old - a_i_old)
H = min(C, C + a_j_old - a_i_old)
else:
L = max(0, a_i_old + a_j_old - C)
H = min(C, a_j_old + a_i_old)
# 一对aiaj迭代了之后,范围也要更新
a_j_new = clip(a_j_new, L, H)
a_i_new = a_i_old + y_i*y_j*(a_j_old - a_j_new)
if abs(a_j_new - a_j_old) < 0.00001:
#print('WARNING alpha_j not moving enough')
continue
alphas[i], alphas[j] = a_i_new, a_j_new
# 更新阈值b
b_i = -E_i - y_i*K_ii*(a_i_new - a_i_old) - y_j*K_ij*(a_j_new - a_j_old) + b
b_j = -E_j - y_i*K_ij*(a_i_new - a_i_old) - y_j*K_jj*(a_j_new - a_j_old) + b
if 0 < a_i_new < C:
b = b_i
elif 0 < a_j_new < C:
b = b_j
else:
b = (b_i + b_j)/2
pair_changed += 1
print('第{}次迭代 pair_changed:{}'.format(it, pair_changed))
if pair_changed == 0:
it += 1
else:
it = 0
print('迭代次数: {}'.format(it))
return alphas, b
if '__main__' == __name__:
# 生成测试数据
a = 200 # 样本数
dataset, labels = make_blobs(n_samples=a, centers=2, n_features=2, random_state=2)
labels[labels == 0] = -1
# 使用简化版SMO算法优化SVM
alphas, b = simple_smo(dataset,labels,0.6,20)
# print('参数alphas: {}'.format(alphas))
# 分类数据点
classified_pts = {'+1':[], '-1':[]}
for point, label in zip(dataset, labels):
if label == 1.0:
classified_pts['+1'].append(point)
else:
classified_pts['-1'].append(point)
# print(classified_pts.items())
fig = plt.figure() # 创建一个子图plt.figure(figsize = (5,5))
ax = fig.add_subplot(111)
# 绘制数据点
for label, pts in classified_pts.items():
pts = np.array(pts)
ax.scatter(pts[:,0],pts[:,1], label = label)
# 绘制分割线
w = get_w(alphas,dataset,labels)
x1, _ = max(dataset, key=lambda x: x[0]) #在样本点第1列数的最大值[1,3] =3
x2, _ = min(dataset, key=lambda x: x[0])
w1, w2 = w # w=(3,4)
y1, y2 = (-b - w1*x1)/w2, (-b - w1*x2)/w2
ax.plot([x1,x2],[y1,y2],c='black')
# 绘制支持向量
for i, alpha in enumerate(alphas): # 遍历alphas
if abs(alpha) > 1e-3:
x, y = dataset[i]
ax.scatter([x],[y],s=50,c='r',marker="v" )
plt.show()
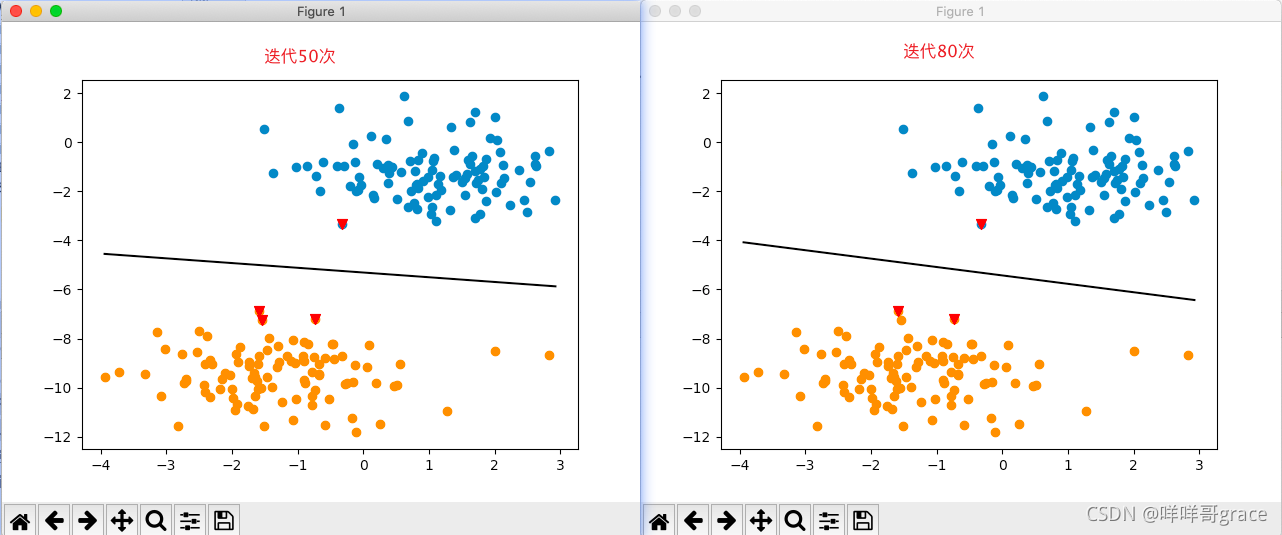
下面运行代码,分别是迭代了50次和80次的效果,其中红色三角符就是支持向量,即离超平面最近的点:
有些图是借鉴,侵则删!