【题目设置】:
难度:中等
链接:https://leetcode-cn.com/problems/valid-sudoku/
题目描述:
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:

输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true
示例 2:
输入:board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
- board.length == 9
- board[i].length == 9
- board[i][j] 是一位数字或者 ‘.’
【解题思路】
解法一:
这道题我们首先想到的就是遍历数组,用三个数组分别来存储每一行、每一列、每一个子九宫格的数据重复情况;判断数据重复,我们想到用HashSet来存储,但此处需要判重的数据是1-9的有限范围内的数字,我们也可以考虑使用一维数组来存储,数组中每一位用true 或false 表示该位置下标的数字是否已经存在;
这样,每一行都用一个长度为9的数组来存储,总共9行,需要一个99的二维数组来存储;同理,每一列的数据重复状态、每一个子九宫格的数据重复状态也需要一个99的二维数组来存储;遍历初始二维数组,对每个数据分别判断三个数组中对应的位置是否为true(该位置是否应存在某数字),如果已经存在,则表示该行/该列/该子九宫格出现重复数字,则初始九宫格为无效;否则将该位置设置为true;
show me the code!
class Solution {
public boolean isValidSudoku(char[][] board) {
boolean[][] rowFlag = new boolean[9][9];
boolean[][] colFlag = new boolean[9][9];
boolean[][] gridFlag = new boolean[9][9];
for (int i = 0; i < 9; i++){
for (int j = 0; j<9; j++){
if (board[i][j] != '.'){
int tmp = board[i][j] - '1';
//如果第i行的tmp数字已经出现过,即rowFlag[i][tmp]==true;则无效
if (rowFlag[i][tmp]){
return false;
}else {
rowFlag[i][tmp] = true;
}
//如果第j列的tmp数字已经出现过,即colFlag[j][tmp]==true;则无效
if (colFlag[j][tmp]){
return false;
}else {
colFlag[j][tmp] = true;
}
//如果第(i/3 * 3 + j/3)个子九宫格中tmp数字已经出现过,即rowFlag[i][tmp]==true;则无效
if (gridFlag[i/3 * 3 + j/3][tmp]){
return false;
}else {
gridFlag[i/3 * 3 + j/3][tmp] = true;
}
}
}
}
return true;
}
}
解法二:
以上方法需要使用3个二维数组来保存每一行、每一列、每一个子九宫格的状态,能否只使用3个一维数组来保存,即令每个数组都可以重复使用;这需要分析我们遍历的顺序,保证每次遍历,都满足同时遍历完某一行所有数据、某一列所有数据、某一个子九宫格所有数据,这样在遍历第二趟,就全都轮到下一行、下一列和下一个子九宫格,之前的三个一维数组就可以清空重复使用;
那么好,对某一行和某一列同时遍历,我们想到在 i 和 j 的双重for循环里取board[i][j] 和board[j][i]分别表示对 i 行遍历和对 i 列进行遍历;
重点是用哪个来表示对第k个子九宫格进行遍历呢?
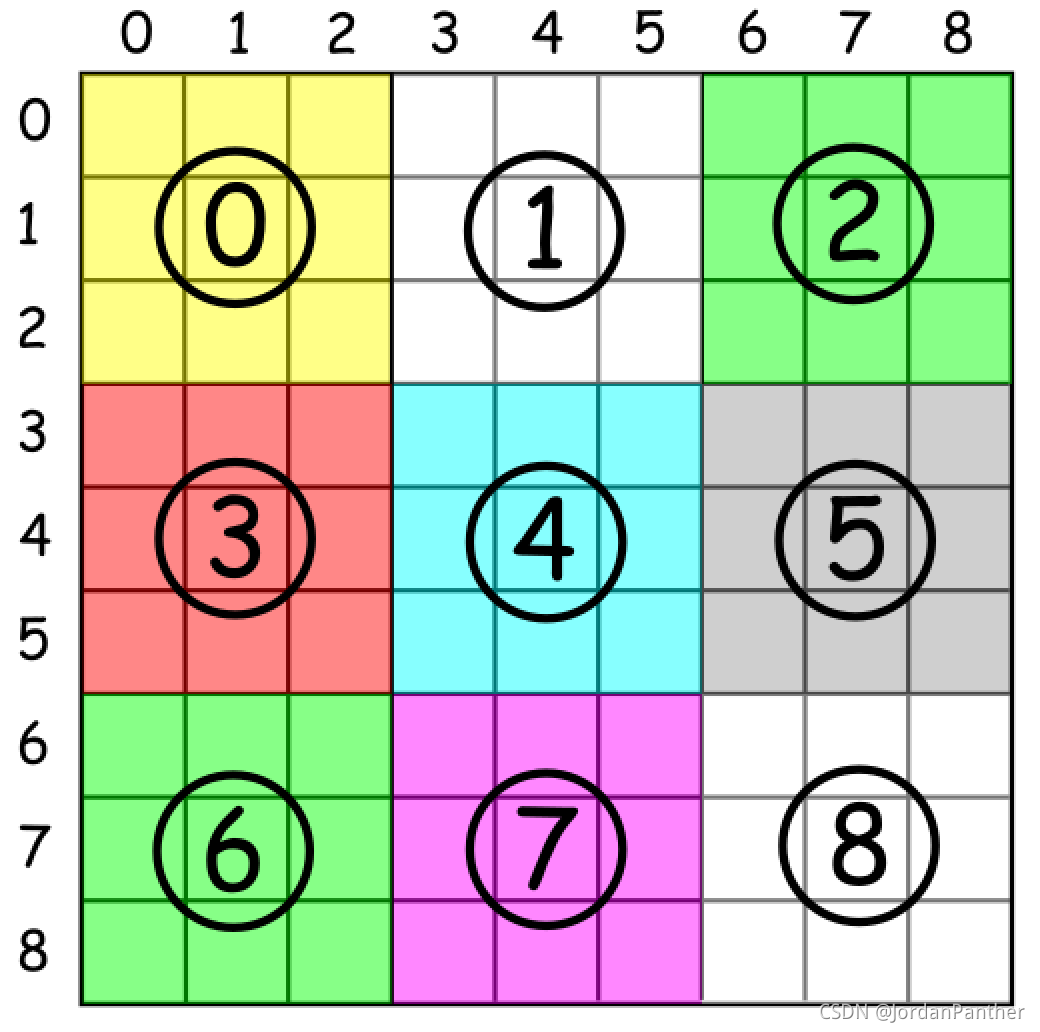
如下图,我们可以用以下公式表示:
board[i % 3 * 3 + j / 3][i / 3 * 3 + j % 3]
这样,当i=0,j 从0遍历到8,都能确保以上位置都是在第0个子九宫格遍历,同理,i=1,j 从0遍历到8,都能确保以上位置都是在第3个子九宫格遍历;
为了好复用每次遍历的存储结构,我们将一维数组换成HashSet(一维数组每次清空都需要再次遍历);
show me the code!
class Solution {
public boolean isValidSudoku(char[][] board) {
Set<Character> rowSet = new HashSet<>();
Set<Character> colSet = new HashSet<>();
Set<Character> gridSet = new HashSet<>();
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
// 行校验
if (board[j][i] != '.' && !rowSet.add(board[j][i]))
return false;
// 列校验
if (board[i][j] != '.' && !colSet.add(board[i][j]))
return false;
// 九宫格校验
if (board[i % 3 * 3 + j / 3][i / 3 * 3 + j % 3] != '.' && !gridSet.add(board[i % 3 * 3 + j / 3][i / 3 * 3 + j % 3]))
return false;
}
rowSet.clear();
colSet.clear();
gridSet.clear();
}
return true;
}
}