1、基础数据结构
1.1数据结构种类
数组
栈
队列和双端队列
链表
集合
字典和散列表
递归
树
二叉堆和堆排序
在写每个知识点的时候 我自己总结的方式是按照定义>javascript实现方式>对应的方法>算法实现的结构去写的 后面有想法在继续补充
1.2 数组
1.2.1 数组定义
js数组其实就是API的调用 是一种最简单的内存数据结构 数组存储一系列同一种数据类型的值
注:javascript中数组可以保存不同类型的值 但是一般不推荐哈
1.2.2 数组创建
在javascript中有两种创建数组的方式
1.使用Array构造函数
let shuzu=new Array();
注意:括号里面参数可以有参数,若为一个数字,表示该数组的长度,如果为多个数字或者一个(多个)非数字表示的是传递数组中应该包含的值。
2.使用数组字面量
let shuzu=[];
1.2.3 数组方法
添加元素 (首尾)
删除元素(首尾)
1、在数组末尾添加元素
使用push方法
numbers.push(11);
原生的方法:
numbers[numbers.length] = 10;
在Javascript中,数组是可以修改的对象,如果要添加元素,会动态生长,所以直接赋值给数组最后一个空位即可
2、在数组开头插入元素
使用unshift方法
numbers.unshift(10);
3从数组末尾删除元素
使用pop方法;
numbers.pop();
4、数组开头删除元素
使用shif方法
number.shif();
5、任意位置添加或者删除元素
使用splice方法:
splice接受多个参数
number.splice(4.,0,6,4)
第一个参数标识要删除或者插入的元素索引值
第二个参数是删除元素的个数,这个例子我们要添加元素所以第二个删除元素的个数为0.
第三个参数往后,就是我们 要添加到数组里面的值
1.2.4 数组的扩展
二维数组本质上是以数组作为数组元素的数组,即“数组的数组”,
类型说明符 数组名[常量表达式][常量表达式]。二维数组又称为矩阵,
行列数相等的矩阵称为方阵。对称矩阵a[i][j] = a[j][i],
对角矩阵:n阶方阵主对角线外都是零元素
var arr = [[1,2],[‘a’,‘b’]];
console.log(arr[1][0]); //a 第2列第1行所在的元素
1.2.5 javascript常用的数组方法
1、concat(),连接两个或者更多的数组,并返回一个新的数组**
2、ES6:copyWithin(),从数组的指定位置复制元素到数组的指定位置。语法:array.copyWithin(target, start, end)
3、ES6:entries(),返回数组的迭代对象
4、every(),检测数组所有元素是否都符合指定条件,接收一个函数作为参数,用于检测数组中的元素
5、ES6:fill(),将一个固定的值替换数组里面的元素。语法:array.fill(value, start, end)
6、filter(),返回一个数组,里面包含符合条件的元素
7、find(),返回数组中符合条件的第一个元素
8、findIndex(),返回数组中符合条件的第一个元素的所在位置
9、forEach(),数组每个元素都执行一次回调函数
10、ES6:from(),将伪数组转换为真正的数组
11、ES6:includes(),判断数组中是否函数指定的值,如有返回true,否则返回false
12、indexOf(),返回数组中指定元素的位置,如果数组中没有指定的元素则返回-1
13、isArray(),判断一个对象是否为数组,是 返回true,不是 返回false
15、ES6:keys(),从数组创建一个包含数组键的可迭代对象
16、lastIndexOf(),返回指定的元素在数组中最后出现的位置,在数组的后面开始搜索
17、map(),返回一个新数组,数组中的元素是原始数组的元素调用函数之后处理的值
18、pop(),删除数组的最后一个元素,并返回删除的元素
19、push(),在数组后面添加新元素,并返回数组新的长度
20、reduce(),将元素的值计算为一个值,从左到右
21、reduceRight(),将元素的值计算为一个值,从右到左
22、reverse(),反转数组元素的排列顺序
23、shift(),删除并返回数组第一个元素
24、unshift(),向数组的最前面添加新元素,并返回新的数组长度
25、slice(),返回指定的数组元素,第一个参数是开始的位置,第二个是结束位置(不包含结束位置的元素)
26、splice(),添加和删除数组中的元素,第一个参数是要删除的元素的开始位置,第二个参数是要删除的元素的个数。第三个以及以后的参数都是添加到数组中的新元素
27、some(),检测数组中是否含有指定的元素,有的话就返回true,没有就返回false
28、sort(),对数组进行排序,可以接收一个比较函数
29、toString(),将数组转为字符串,并返回结果
30、valueOf(),返回数组对象的原始值
常用的我已经加粗了!!!
1.2.6 类型数组
由于javascript与c和Java等语言不同,javascript数组不是强类型。可以存储任意类型数据
那么如何让javascript的数组也存储单一的数据类型呢?
这个就用到类型数组。
具体语法:
let myArray = new TypedArray(length)
//在实际使用中 把TypedArray换成下面列表中需要的类型
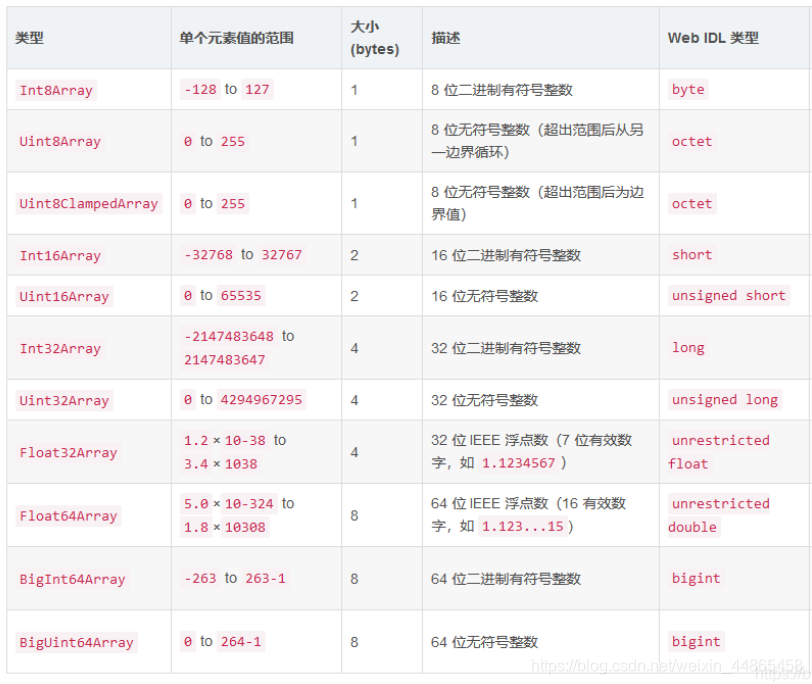
1.2.7TypeScript中的数组
Typescript中最简单的方法是使用「类型 + 方括号」来表示数组
let fibonacci: number[] = [1, 1, 2, 3, 5];
数组的项中不允许出现其他的类型:
在使用数组方法时,对应增删改查的元素类型必须一致,否则会报错。
详解文章:
TypeScript 数组Array操作
1.3 栈
1.3.1 概述
栈是一种遵从先进后出(LIFO)原则的有序集合。
新添加或待删除的元素都保存在栈的末尾,称作栈顶,另一端就叫栈底。
在栈里,新元素都靠近栈顶,旧元素都接近栈底
用日常生活中的例子:
栈就像我们的衣服口袋,先放进去的东西后取出来,后放进去的东西能先取出来
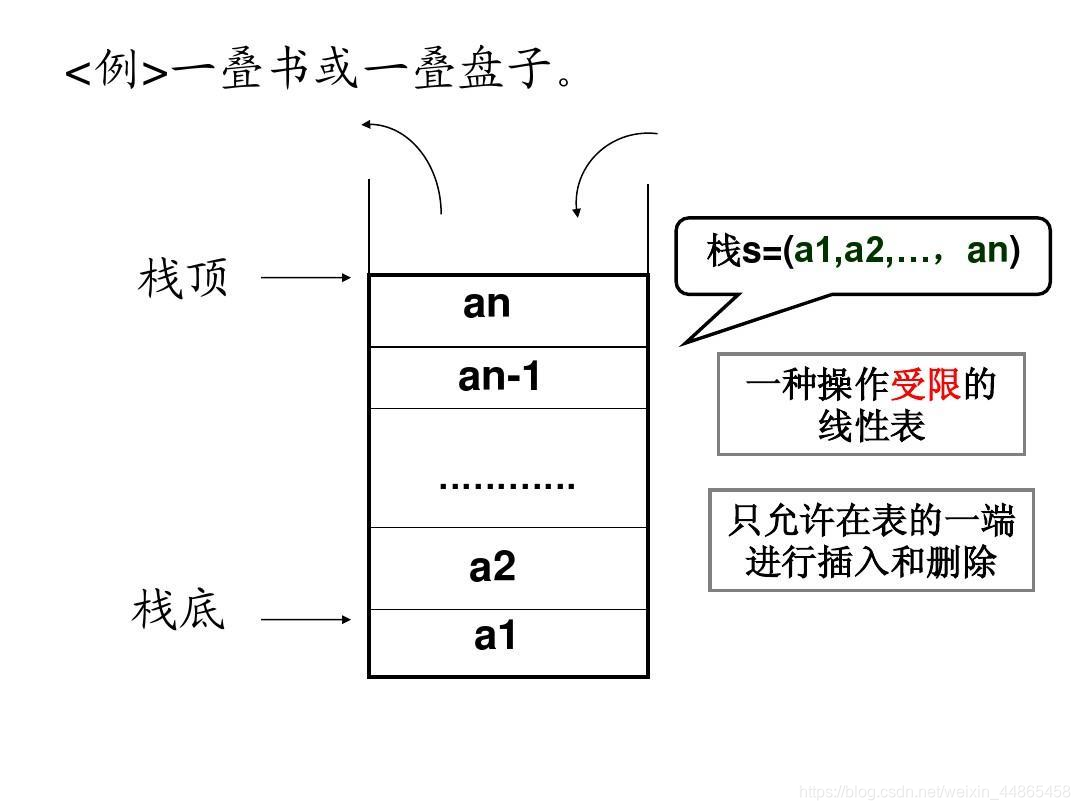
栈被用在编程语言的编译器和内存中用于保存变量,方法调用等等,也被用于浏览器历史记录(浏览器的返回按钮)
1.3.2 基于javascript数组创建栈
在javascript中用数组创建一个栈一共7个步骤:
1、先声明一个stack类,用于存放栈
2、向栈中使用push添加元素(只能从栈顶添加)
3、从栈中使用pop方法移除元素(从栈顶移除)
4.查看栈顶元素(peek方法)
5.检查栈是否为空 方法为isEmpty 如果栈为空返回true 否则返回false
6.使用clear方法清空栈元素
7.可以开始使用stack类
经过上面的六步,stack已近具有了栈的特点。
代码实现:
//创建一个基于数组单位栈
class stack{
constructor{
this.items = [];
}
}
//向栈中使用push方法添加元素
push () {
this.items.push();
}
// 使用pop方法从栈顶移除元素
pop(){
reyurn this.items.pop();
}
//经过上面这两个步骤,基本实现了栈的先进后出的原则
//查看栈顶元素 (length -1)
peek{
return this.items{this.items.length - 1};
}
//使用isEmpty检查栈是否为空
isEmpty(){
return this.items.length === 0;
}
//完成上面的步骤后,使用clear方法清除栈里面的所有元素
clear(){
return this.items.length;
}
//至此。栈已经完成了
就可以使用栈的方法来对栈进行操作了
1.3.3 基于javascript对象创建栈
前面我们已经学会使用数组来创建栈了,但在实际的应用中,处理大量数据的时候,需要评估如何使用数据是最高效的,使用数组的时间复杂度为0(n),n代表数组的长度,因为数组是一个有序集合,为了保证元素排序,会占用更多的内存我们需要迭代整个数组直到寻找到目标元素。
由此引出了对象创建栈
对象能直接获取元素,占用较少的内存空间,而且能够按照我们的要求排列数据。
操作步骤一共六步:
1、声明一个stack类
2、向栈中插入元素
3、验证栈是否为空和它的大小
4、从栈中弹出元素
5、查看栈值并将栈清空
6、创建tostring方法
代码实现:
//首先声明一个stack类
class stack {
constructor () {
this.count = 0 ; //使用count来记录栈的大小,也能帮助我们删除和添加元素
this.items = {};
}
}
//向栈中加入元素
push(element) {
this.items[this.count ] = element;
this.count ++ ;
}
//在js中,对象是键值对的形式表现出来,我们使用count作为items对象的键名,插入的元素则是它的值,插入元素后,我们把count++,以便于下一个变量值插入
//count属性也表示栈的大小,我们可以返回count的size来计算栈的大小
size(){
return this.count;
}
//验证栈是否为空
isEmpty(){
return this.count === 0;
}
//查看栈顶的值并将栈清空
peek{
if (this.isEmpty()){
return unerfined;
}
return this.items{this.items.length - 1};
}
//清空栈把值变为构造函数的初始值就ok
clear (){
this.items = {};
this.count = 0;
}
//也可以使用另外一种方法:
while (!this.isEmpty()){
this.pop();
}
//创建tostring方法
在前面的数组中没有提string方法,是因为数组内置就有tostring属性,使用对象的时候,就需要我们手动去穿件了
toString () {
if (this.isEmpty()){
return '';
}
let objStru=ing = '${this.items[0]}';
for (let i = 1 ; i < this.count; i++ ){
objString = '${objstring},${this.items[i]}';
}
return objstring ;
}
//如果栈是空的,返回空值就ok了
//如果不是空的。底部第一个元素作为字符串的初始值,然后迭代整个栈
至此,一个基于对象创建的栈就完成了
1.3.4 保护数据结构内部元素
在我们创建一个栈后,别的同事也可能要使用,我们想保护内部的元素,只允许改变我们暴露的元素,这个时候就提及到了保护数据结构内部元素:
主要有三种方法:
1、下划线命名约定
下划线命名定义
一部分开发者喜欢在javascript中使用下划线命名约定来标记一个属性为私有属性
下划线命名约定实在属性名称之间加一个下划线-,不过这种方法只是一种约定,不能保护数据,看不懂的程序员就gg了
代码实现:
class stack {
constructor () {
this._count = 0;
this._items = {};
}
}
2、symbol实现类
使用symbol实现类
在es6中规定,symbol是不可变的,可以用作对象的属性
代码实现:
cosnt_items = symbol('stacItems');
class stack {
constoructor () {
this[_items] = [];
}
//栈的方法
}
3、使用weakMap实现类
使用weakMap实现类
weakMap就能确保属性私有,weakMap是键值对的存在,键是对象,值是属性。
1.3.5 javascript中用栈解决实际问题
使用栈实现阶乘的递归
使用栈来模拟5!的过程,首先将数字5到1压入栈,然后使用一个循环将数字挨个弹出并连乘
代码实现:
1 function fact(num) {
2 var stack=new Stack;
3 while(num>0){
4 stack.push(num--);
5 }
6 var sum=1;
7 while(stack.length>0){
8 sum*=stack.pop;
9 }
10 return sum;
11 }
12
13 console.log(fact(5)) //120
1.3.6 合法括号
下面的字符串中包含小括号,请编写一个函数判断字符串中的括号是否合法,所谓合法,就是括号成对出现
sdf(ds(ew(we)re)rwqw)qwrwq 合法
(sd(qwqe)sd(sd)) 合法
()()sd()(sd()dw))( 不合法
思路分析
括号存在嵌套关系,也存在并列关系,如果使用数组来存储这些括号,然后再想办法一对一的抵消掉,似乎可行。但是我们无法判断一个左括号对应的是哪一个右括号。在数组的角度思考这个问题,就有些困难。
现在,我们使用栈来解决这个问题
遇到左括号,就把做括号压入栈中
遇到右括号,判断栈是否为空,如果为空则说明没有左括号与之相对应,字符串括号不合法。如果栈不为空,则把栈顶元素移除,这对括号就抵消了。
当for循环结束,如果栈是空的,说明所有的左右括号都抵消了,如果栈力还有元素,则说明缺少右括号,字符串括号不合法。
代码实现:
function is_leagl_brackets(string){
var stack = new Stack();
for (var i = 0;i<string.length;i++) {
var item = string[i];
// 遇到做括号入栈
if(item == '('){
stack.push(item)
}else if (item == ')'){
// 遇到右括号,判断栈是否为空
if(stack.isEmpty()){
return false
}else {
stack.pop() // 弹出左括号
}
}
}
// 如果栈为空,说明字符串括号合法
return stack.isEmpty()
}
console.log(is_leagl_brackets('sdf(ds(ew(we)re)rwqw)qwrwq')) // true
console.log(is_leagl_brackets('(sd(qwqe)sd(sd))')) // true
console.log(is_leagl_brackets('()()sd()(sd()dw))(')) // false
实现一个有min方法的栈
供一个min方法,返回栈里的最小的元素,且时间复杂度为O(1)
function MinStack() {
var data_stack = new Stack();
var min_stack = new Stack();
// 用min_stack 记录每次 push 进来的元素之后,栈中的最小值
this.push = function (item) {
data_stack.push(item);
if(min_stack.isEmpty() || item < min_stack.top()){
min_stack.push(item)
}else {
min_stack.push(min_stack.top())
}
};
// 这样,每次pop之后,min_stack 也会将上次栈中的最小值弹出
this.pop() = function () {
data_stack.pop()
min_stack.pop()
}
this.min = function () {
return min_stack.top()
}
}
实际应用中还有许多,这里我就不挨个列举 了。
1.4 队列和双端队列
1.4.1队列数据结构
1、队列的概念:
队列遵循的是先进先出原则的一组有序的列。队列在尾部添加元素,顶部移除元素。
联系到日常生活中排队付款,买菜,后面加人排队,前面的人付款先走。
2、队列的创建:
1、使用一个类来创建队列
class Queue { constructor() { this.count = 0; this.lowestCount = 0;//追踪队列的第一个元素 this.items = {}; }
2.使用enqueue方法向队列中添加元素(添加在队列末尾)
enqueue(element) { this.items[this.count] = element; this.count++; }
3、使用dequeue方法从队列中删除元素(从队列顶部移除)
size() { return this.count - this.lowestCount; };isEmpty() { return this.size() === 0; };
4、查看队列最前面的项(使用peek方法)
peek() { if (this.isEmpty()) { return undefined; } return this.items[this.lowestCount]; }
5、使用isEmpty方法检查队列是否为空和获取他的长度
6.清空队列
clear() { this.items = {}; this.count = 0; this.lowestCount = 0; }
7.创建tostring方法
toString() { if (this.isEmpty()) { return ‘’; } let objstring =${this.items[this.lowestCount]}; for (let i = this.lowestCount + 1; i < this.count; i++) { objstring =${objString},${this.items[i]}; } return objString; }
创建方法根据队列的原理和前面讲到得栈相似,这里我就不重复了
1.4.2 双端队列数据结构(deque)
1、双端队列的概念:
双端队列是一种允许我们同时从队列的前端和后端添加和移除元素的特殊队列
在计算机中双端队列常见的应用是储存一系列的撤销操作,用户在撤销后,该操作会被存储在一个双端队列中,可以点击撤销和烦撤销,
由于双端队列同时遵守了先进先出和后进先出的原则,可以说他是把队列和栈结合的一种数据结构。
2、双端队列的创建:
1、 创建双端队列
class Deque { constructor() { this.count = 0; this.lowestCount = 0; this.items = {}; }
2、队首添加元素
addFront(element) { if (this.isEmpty()) {//空队列 this.addBack(element); } else if (this.lowestCount > 0) {//之前被删除,重新添加 this.lowestCount–; this.items[this.lowestCount] = element; } else { for (let i = this.count; i > 0; i–) { this.items[i] = this.items[i - 1]; } this.count++; this.items[0] = element; } }
3、 队尾添加元素
addBack(element) { this.items[this.count] = element; this.count++; }
4、队首删除元素
removeFront() { if (this.isEmpty()) { return undefined; } const result = this.items[this.lowestCount]; delete this.items[this.lowestCount]; this.lowestCount++; return result; }
5、队尾删除元素
removeBack() { if (this.isEmpty()) { return undefined; } this.count–; const result = this.items[this.count]; delete this.items[this.count]; return result; }
6、返回队首元素
peekFront() { if (this.isEmpty()) { return undefined; } return this.items[this.lowestCount]; }
7、返回队尾元素
peekBack() { if (this.isEmpty()) { return undefined; } return this.items[this.count - 1]; }
1.4.3队列和双端队里的应用
模拟击鼓传花游戏
情景:孩子们围城一圈,把花传递给身边的人,某一时刻停止,花在谁手上,谁就推出。重复这个操作,剩下的最后一个人就是胜利者。
代码实现:
function hotPotato(elementsList, num) { const queue = new Queue(); const elimitatedList = [];
for (let i = 0; i < elementsList.length; i++) { queue.enqueue(elementsList[i]); }
while (queue.size() > 1) { for (let i = 0; i < num; i++) { queue.enqueue(queue.dequeue()); } elimitatedList.push(queue.dequeue()); }
return { eliminated: elimitatedList, winner: queue.dequeue() };}
回文检查器
检查一个词组挥着字符串是否为回文。
代码实现:
function palindromeChecker(aString) { if ( aString === undefined || aString === null || (aString !== null && aString.length === 0) ) { return false; } const deque = new Deque(); const lowerString = aString.toLocaleLowerCase().split(' ').join(''); let firstChar; let lastChar;
for (let i = 0; i < lowerString.length; i++) { deque.addBack(lowerString.charAt(i)); }
while (deque.size() > 1) { firstChar = deque.removeFront(); lastChar = deque.removeBack(); if (firstChar !== lastChar) { return false; } }
return true;};
1.5 链表
1.5.1 链表概述(LinkedList)
链表存储有序的元素集合,但不同于数组,链表中的元素在内存中并不是连续放置的。每个元素由一个存储元素本身的节点和一个指向下一个元素的引用(也称为指针或链接)组成。下图讲解:
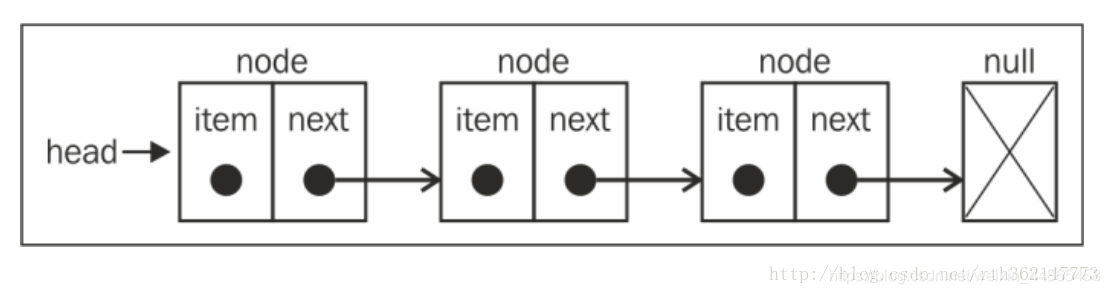
相对于传统的数组,链表的一个好处在于,添加或移除元素的时候不需要移动其他元素。然而,链表需要使用指针,因此实现链表的时候需要注意。数组的另一个细节是可以直接访问任何位置元素,而要想访问链表中间的一个元素,需要从起点(表头)开始送达列表直到找到所需要元素。
现实实例就是火车,火车有多节车厢相互衔接,通过接轨来链接火车。车厢就是链表的元素,而接轨就是指针。

1.5.2 创建链表
function LinkedList() {
var Node = function (val) { //新元素构造
this.val = val;
this.next = null;
};
var length = 0;
var head = null;
this.append = function (val) {
var node = new Node(val); //构造新的元素节点
var current;
if (head === null) { //头节点为空时 当前结点作为头节点
head = node;
} else {
current = head;
while (current.next) { //遍历,直到节点的next为null时停止循环,当前节点为尾节点
current = current.next;
}
current.next = node; //将尾节点指向新的元素,新元素作为尾节点
}
length++; //更新链表长度
};
this.removeAt = function (position) {
if (position > -1 && position < length) {
var current = head;
var index = 0;
var previous;
if (position == 0) {
head = current.next;
} else {
while (index++ < position) {
previous = current;
current = current.next;
}
previous.next = current.next;
}
length--;
return current.val;
} else {
return null;
}
};
this.insert = function (position, val) {
if (position > -1 && position <= length) { //校验边界
var node = new Node(val);
current = head;
var index = 0;
var previous;
if (position == 0) { //作为头节点,将新节点的next指向原有的头节点。
node.next = current;
head = node; //新节点赋值给头节点
} else {
while (index++ < position) {
previous = current;
current = current.next;
} //遍历结束得到当前position所在的current节点,和上一个节点
previous.next = node; //上一个节点的next指向新节点 新节点指向当前结点,可以参照上图来看
node.next = current;
}
length++;
return true;
} else {
return false;
}
};
this.toString = function () {
var string = head.val;
var current = head.next;
while (current) {
string += ',' + current.val;
current = current.next;
}
return string;
};
this.indexOf = function (val) {
var current = head;
var index = -1;
while (current) {
if (val === current.val) { //从头节点开始遍历
return index;
}
index++;
current = current.next;
}
return -1;
};
this.getLength = function () {
return length;
}
this.getHead = function () {
return head;
}
}
// 创建链表
var li = new LinkedList();
li.append(1);
li.append(2);
li.append(4);
li.append(4);
li.append(5);
li.insert(2,3);
li.insert(2,3);
console.log(li.toString()) // 1,2,3,3,4,4,5
console.log(li.getHead()) // 1->2->3->3->4->4->5
参考链接:
【数据结构】如何在JS中创建一个链表
1.5.3 双向链表
双向列表和普通列表的区别在于:
在单向列表中一个节点只有链向下一个节点的链接,而在双向列表中,链接是双向的一个链接向下一个元素,另一个链向前一个元素。
双向链表:既可以从头遍历到尾,又可以从尾遍历到头。也就是说链表连接的过程是双向的,它的实现原理是:一个节点既有向前连接的引用,也有一个向后连接的引用。
双向链表的缺点:
每次在插入或删除某个节点时,都需要处理四个引用,而不是两个,实现起来会困难些;
相对于单向链表,所占内存空间更大一些;
但是,相对于双向链表的便利性而言,这些缺点微不足道。
如图所示:
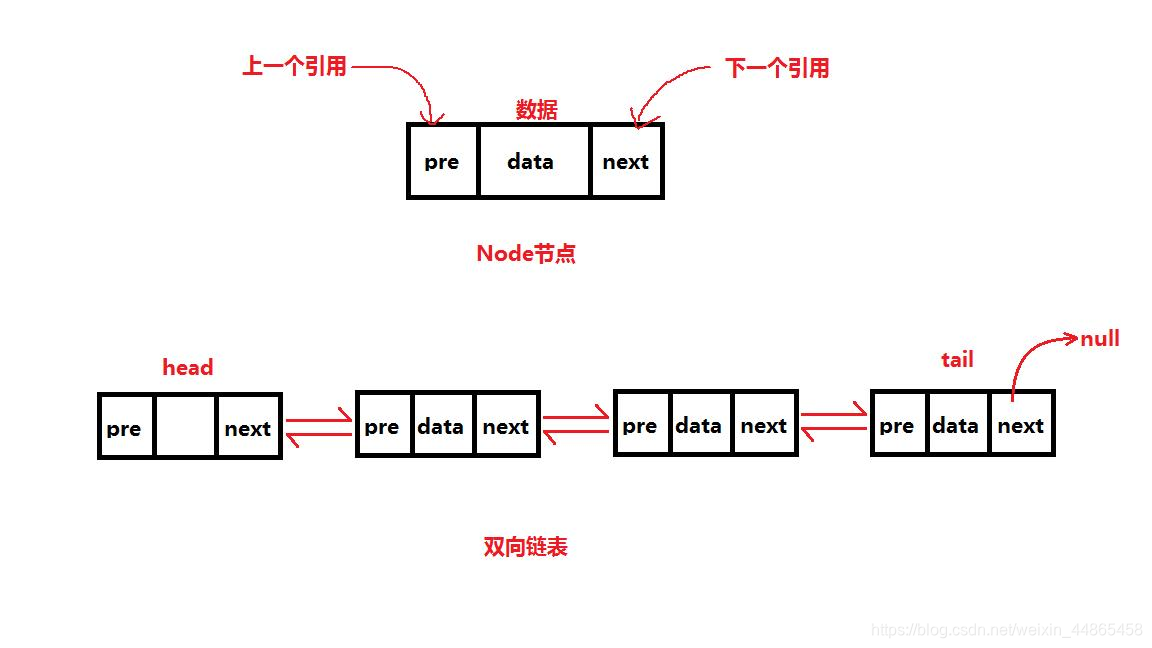
代码实现:
//先创建双向链表类DoubleLinklist,并添加基本属性,再实现双向链表的常用方法:
//封装双向链表类
function DoubleLinklist(){
//封装内部类:节点类
function Node(data){
this.data = data
this.prev = null
this.next = null
}
//属性
this.head = null
this.tail ==null
this.length = 0
}
1.5.4循环链表
双向链表的每个结点需要连接前一个结点和后一个结点,所以需要定义两个指针域,分别指向前一个结点和后一个结点。
双向链表中头节点的prev指针指向尾节点,尾节点的next指针指向头节点。
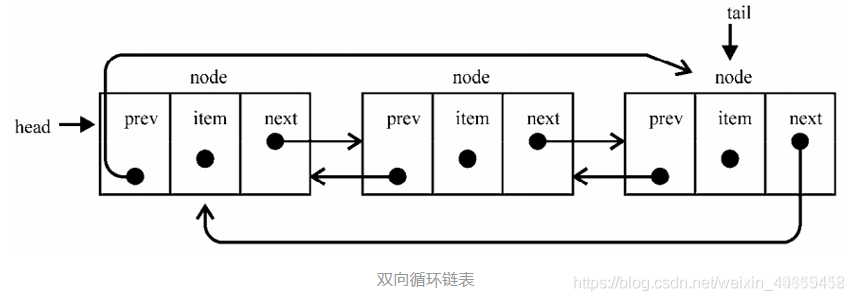
循环列表的实现:
1、创建双向循环链表
function DoublyCircularLinkedList(){
function Node(element){
this.element=element
this.next=null
this.prev=null
}
let length=0
let head=null
let tail=null
}
2、尾部插入新节点
this.append=function(element){
let node = new Node(element)
let current // 当前节点
let previous // 前一个节点
if(!head){
head=node
tail=node
head.prev=tail
tail.next=head
}else{
current=head
while(current.next !== head){
previous = current
current = current.next
}
current.next=node
node.next=head
node.prev=current
}
length++
return true
}
3、任意位置插入节点
// 在任意位置插入一个节点
this.insert=function(position,element){
if(position > 0 && position <= length){
let node = new Node(element)
let index = 0
let current = head
let previous
if(position === 0){ // 头部插入
if(!head){
node.next=node
node.prev=node
head=node
tail=node
}else{
current.prev=node
node.next=current
}
}else if(position === length){ // 在尾部插入
current=tail
current.next=node
node.prev=current
tail=node
node.next=head
}else{
while(index++ < position){
previous=current
current=current.next
}
current.prev=node
node.next=current
previous.next=node
node.prev=previous
}
length++
return true
}else{
return false
}
}
4、根据位置删除节点
this.removeAt = function(position){
if(position > -1 && position < length){
let current = head
let index = 0
let previous;
if(position === 0){
current.next.previous = tail
head = current.next;
}else if(position === length - 1){
current = tail;
current.prev.next = head
head.prev = current.prev
tail = current.prev
}else{
while(index++ < position){
previous = current
current = current.next
}
previous.next = current.next
current.next.prev = previous
}
length--
return true
}else{
return false
}
}
5、根据节点值删除节点
this.remove = function(element){
let current = head
let previous
let indexCheck = 0
while(current && indexCheck < length){
if(current.element === element){
if(indexCheck === 0){
current.next.prev = tail;
head = current.next
}else{
current.next.prev = previous
previous.next = current.next
}
length--
return true
}
previous = current
current = current.next
indexCheck++
}
return false
}
1.5.5有序链表
有序链表是指保持元素有序的链表结构,除了使用排序算法之外,我们还可以将元素插入到正确的位置来保证链表的有序性。
代码实现:
const Compare = {
LESS_THAN:-1,
BIGGER_THAN:1
};
function defaultCompare(a,b){
if(a === b){
return 0;
}
return a < b?Compare.LESS_THAN : Compare.BIGGER_THAN;
}
class SortedLinkedList extends LinkedList{//LinkedList这个类可以见https://www.cnblogs.com/MySweetheart/p/13212220.html
constructor(equalsFn = defaultEquals, compareFn = defaultCompare){
super(equalsFn);
this.compareFn = compareFn;
}
insert(element,index = 0){
if(this.isEmpty()){
return super.insert(element,0);
}
const pos = this.getIndexNextSortedElement(element);
return super.insert(element,pos);
}
getIndexNextSortedElement(element){
let current = this.head;
let i = 0;
for(;i < this.size() && current; i++){
const comp = this.compareFn(element,current.element);
if(comp == Compare.LESS_THAN){
return i;
}
current = current.next;
}
return i;
}
}
1.5.6 用链表实现栈
这点书上讲的比较模糊,可以参考下面这篇文章:
JAVASCRIPT——通过链表实现栈功能
1.7集合
1.7.1 集合的概念特点
在es6中提出了set()方法,它允许创建唯一值的集合,集合是由一组无序且唯一的项组成,是一种不允许重复的数据结构。集合中的元素可以是简单的数据,也可以是复杂的对象,可以把它理解称为没有重复数据的数组。
特点:
不允许重复的顺序数据结构
语法:
new Set([iterable]);
1.7.2集合创建
1、声明一个set类
2、add(element):向集合中添加一个新元素
3、delete(element):从集合中删除一个元素
4、has(element):如果元素在集合中,返回true ,否则返回false
5、clear():清除集合中的所有元素
6、size():返回集合中包含元素的数量,与数组中的length属性类似
7、values():返回一个包含集合中所有值的(元素)的数组代码实现:
class Set {
constructor () {
this.items = {};
}
add (value) { // 向集合中添加元素
if (!this.has(value)) {
this.items[value] = value;
return true;
}
return false;
}
delete (value) { // 从集合中删除对应的元素
if (this.has(value)) {
delete this.items[value];
return true;
}
return false;
}
has (value) { // 判断给定的元素在集合中是否存在
return this.items.hasOwnProperty(value);
}
clear() { // 清空集合内容
this.items = {};
}
size () { // 获取集合的长度
return Object.keys(this.items).length;
}
values () { // 返回集合中所有元素的内容
return Object.values(this.items);
}
}
1.7.3集合运算
集合运算在数学中我们就学习过,在计算机中也同样被重视,查询数据库的SQL语句的基础就是集合运算。查询后的数据库也会返回一个数据集合
1.并集
对于给定的两个集合,并集返回一个包含两个集合中所有元素的新集合。
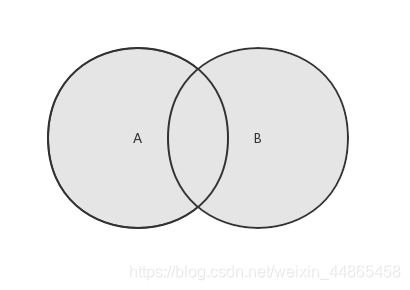
思路:首先遍历第一个集合,将所有的元素添加到新集合中,然后再遍历第二个集合,将所有的元素添加到新集合中。然后返回新集合。不用担心会添加重复的元素,因为集合的add()方法会自动排除掉已添加的元素。
代码实现:
union (otherSet) { // 并集
let unionSet = new Set();
this.values().forEach(value => unionSet.add(value));
otherSet.values().forEach(value => unionSet.add(value));
return unionSet;
}
2.交集
对于给定的两个集合,交集返回一个包含两个集合中共有元素的新集合
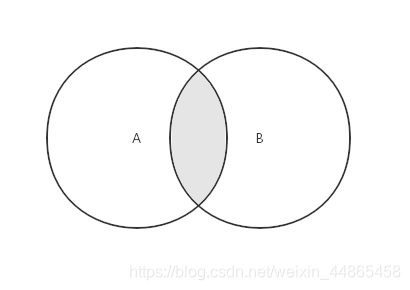
思路:遍历第一个集合,如果元素出现在第二个集合中,则将它添加到新集合。然后返回新集合。
代码实现:
intersection (otherSet) { // 交集
let intersectionSet = new Set();
this.values().forEach(value => {
if (otherSet.has(value)) intersectionSet.add(value);
});
return intersectionSet;
}
3.差集
对于给定的两个集合,差集返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合
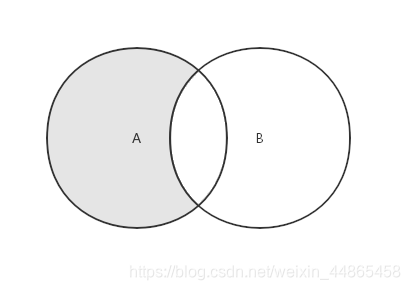
思路:遍历第一个集合,如果元素没有出现在第二个集合中,则将它添加到新集合。然后返回新集合。
代码实现:
difference (otherSet) { // 差集
let differenceSet = new Set();
this.values().forEach(value => {
if (!otherSet.has(value)) differenceSet.add(value);
});
return differenceSet;
}
4.子集
验证一个给定集合是否是另一个集合的子集,即判断给定的集合中的所有元素是否都存在于另一个集合中,如果是,则这个集合就是另一个集合的子集,反之则不是。

思路:
如果集合A比集合B的长度大,则直接返回false,因为这种情况A不可能是B的子集。然后使用every()函数遍历集合A的所有元素,一旦碰到其中的元素没有在集合B中出现,则直接返回false,并终止遍历
代码实现:
subset (otherSet) { // 子集
if (this.size() > otherSet.size()) return false;
let isSubset = true;
this.values().every(value => {
if (!otherSet.has(value)) {
isSubset = false;
return false;
}
return true;
});
return isSubset;
}
1.8 字典和散列表
1.8.1字典的概念和特点
在上一章中我们讲到集合:表示一组不重复的数据,字典和集合的主要区别就在于,集合中数据是以[值,值]的形式保存的,我们只关心值本身;而在字典和散列表中数据是以[键,值]的形式保存的,键不能重复,我们不仅关心键,也关心键所对应的值
字典也被称为:映射,符号表,关联数组。
1.8.2字典创建
创建方法:
set(key,value ):向字典中添加新元素。如果key存在,那么已经存在的value值也会被新值覆盖
remove(key):通过使用键值作为参数来从字典中移除对应的数据值
hasKey(key):如果某个键值存在于字典中,返回true,否则返回false
get(key):通过以键值作为参数查找特定的数值并返回
clear():删除该字典中的所有值
size():返回字典中所有值的数量,与数组中的length类似
isEmpty():在size等于零的时候返回true,其他时候返回false
keys():将字典中所有的键名以数组的形式返回
values():将字典中所有的键值以数组的形式返回
keyValues():将字典中所有的【键,值】返回
forEach(callbackFn):迭代字典中的所有键值对,有两个参数:key和value
代码实现:
class Dictionary {
constructor () {
this.items = {};
}
set (key, value) { // 向字典中添加或修改元素
this.items[key] = value;
}
get (key) { // 通过键值查找字典中的值
return this.items[key];
}
delete (key) { // 通过使用键值来从字典中删除对应的元素
if (this.has(key)) {
delete this.items[key];
return true;
}
return false;
}
has (key) { // 判断给定的键值是否存在于字典中
return this.items.hasOwnProperty(key);
}
clear() { // 清空字典内容
this.items = {};
}
size () { // 返回字典中所有元素的数量
return Object.keys(this.items).length;
}
keys () { // 返回字典中所有的键值
return Object.keys(this.items);
}
values () { // 返回字典中所有的值
return Object.values(this.items);
}
getItems () { // 返回字典中的所有元素
return this.items;
}
}
1.8.4散列表的概念和特点
散列表(或者叫哈希表),是一种改进的dictionary,它将key通过一个固定的算法(散列函数或哈希函数)得出一个数字,然后将dictionary中key所对应的value存放到这个数字所对应的数组下标所包含的存储空间中。在原始的dictionary中,如果要查找某个key所对应的value,我们需要遍历整个字典。为了提高查询的效率,我们将key对应的value保存到数组里,只要key不变,使用相同的散列函数计算出来的数字就是固定的,于是就可以很快地在数组中找到你想要查找的value。下面是散列表的数据结构示意图:
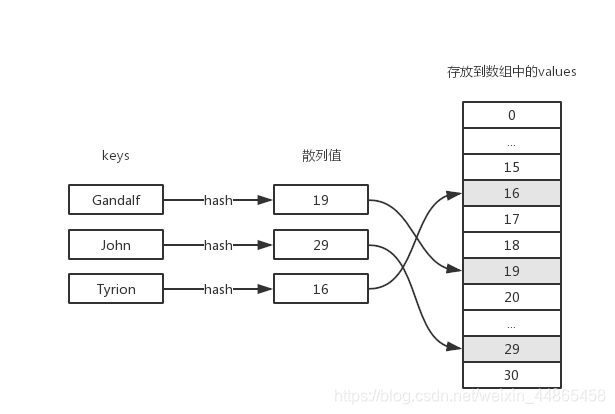
1.8.4 散列表的实现
lose lose 散列函数是比较简单的一种:把每个键值对中的每个字母的ASCII值相加
下面是散列函数loseloseHashCode()的实现代码:
loseloseHashCode (key) {
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash += key.charCodeAt(i);
}
return hash % 37;
}
这个散列函数的实现很简单,我们将传入的key中的每一个字符使用charCodeAt()函数(有关该函数的详细内容可以查看这里)将其转换成ASCII码,然后将这些ASCII码相加,最后用37求余,得到一个数字,这个数字就是这个key所对应的hash值。接下来要做的就是将value存放到hash值所对应的数组的存储空间内。下面是我们的HashTable类的主要实现代码:
class HashTable {
constructor () {
this.table = [];
}
loseloseHashCode (key) { // 散列函数
let hash = 0;
for (let i = 0; i < key.length; i++) {
hash += key.charCodeAt(i);
}
return hash % 37;
}
put (key, value) { // 将键值对存放到哈希表中
let position = this.loseloseHashCode(key);
console.log(`${position} - ${key}`);
this.table[position] = value;
}
get (key) { // 通过key查找哈希表中的值
return this.table[this.loseloseHashCode(key)];
}
remove (key) { // 通过key从哈希表中删除对应的值
this.table[this.loseloseHashCode(key)] = undefined;
}
isEmpty () { // 判断哈希表是否为空
return this.size() === 0;
}
size () { // 返回哈希表的长度
let count = 0;
this.table.forEach(item => {
if (item !== undefined) count++;
});
return count;
}
clear () { // 清空哈希表
this.table = [];
}
}
1.9 递归
1.9.1理解递归
一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。
简单来说就是自己调用自己,把大的问题切分成小的模块解决
1.9.2 计算一个n的阶乘
1、使用循环的方法计算n的阶乘
function xunhuan (number) {
if (number<0,) return underfind;
let tatal = 1;
for (let n = 1, n> 1,n++){
total = total *n;
}
return total ;
}
console.xunhuan(10)
//计算10的阶乘
2、使用递归的方法计算n的阶乘
function factorial (n) {
if ( n === 1 || n === 0){
return 1;}
return n*factorial(n-1);
}
console.log(factorial(10))
//计算10的阶乘
1.9.3斐波那契数列
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N)*
总结来说就是第一第二个数是1 ,后面每个数是前两个数之和
三种计算方法
迭代
递归
记忆求解(缓存出现过两次的计算值 把之前求的值都记录下来)
迭代:
function Fibo(n) {
if(n <= 0) {
return -1;
}
if(n <= 2) {
return 1;
}
let pre = 1; //第一次循环pre是f(1)也就是1
let next = 1; //第一次循环next是f(2)也就是1
let n_value = 0; // 保存f(n)的值
for(let i = 3; i <= n; i++) {
n_value = pre + next; //每一次循环n_value就是前两个数的和
pre = next; // 然后把next赋值给pre
next = n_value; //把新的n_value的值赋值给next
}
return n_value;
}
递归:
function Fibo(n) {
if(n <= 0) {
return -1; //输入的n不合法,返回-1
}
if(n <= 2) {
return 1; // 第一项和第二项为1
} else {
return Fibo(n-2) + Fibo(n-1); // 从第三项开始等于前两项的和
}
}
记忆化:
const fibonacci = (( cache = {} ) => n => {
if( cache[ n ] ){
return cache[ n ];
}
if( n < 2 ){
return cache[ n ] = n;
}
return cache[ n ] = fibonacci( n - 1 ) + fibonacci( n - 2 );
})();
1.10 树
1.10.1 树的基本概念和类型
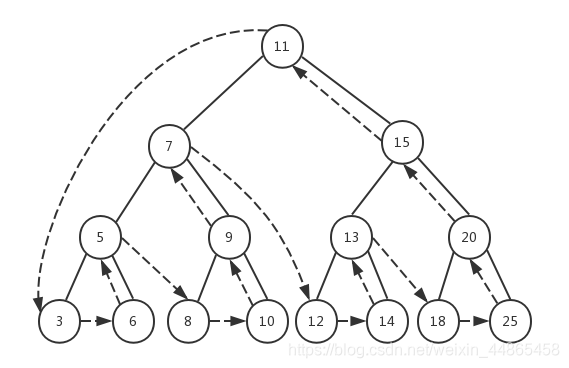
在计算机科学中,树是一种十分重要的数据结构。树被描述为一种分层数据抽象模型,常用来描述数据间的层级关系和组织结构。树也是一种非顺序的数据结构。下图展示了树的定义:
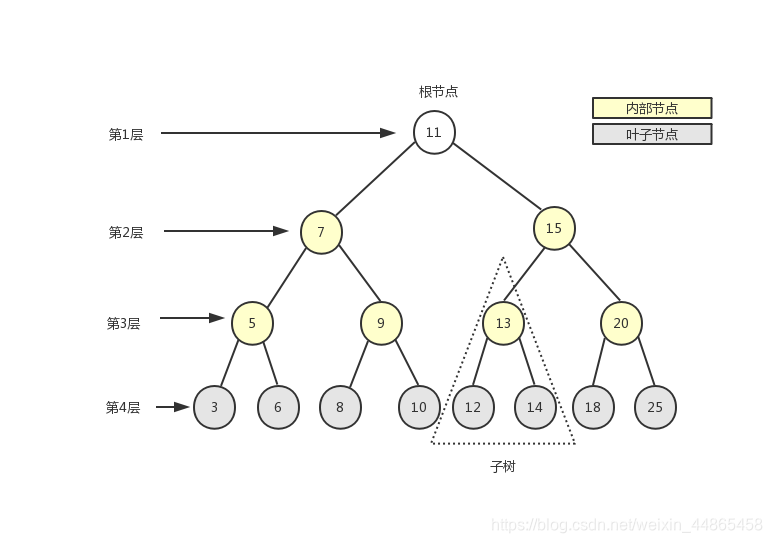
如上图所示,一棵完整的树包含一个位于树顶部的节点,称之为根节点(11),它没有父节点。树中的每一个元素都叫做一个节点,节点分为内部节点(图中显示为黄色的节点)和外部节点(图中显示为灰色的节点),至少有一个子节点的节点称为内部节点,没有子元素的节点称为外部节点或叶子节点。一个节点可以有祖先(根节点除外)和后代。子树由节点本身和它的后代组成,如上图中三角虚框中的部分就是一棵子树。节点拥有的子树的个数称之为节点的度,如上图中除叶子节点的度为0外,其余节点的度都为2。从根节点开始,根为第1层,第一级子节点为第2层,第二级子节点为第3层,以此类推。树的高度(深度)由树中节点的最大层级决定(上图中树的高度为4)。
在一棵树中,具有相同父节点的一组节点称为兄弟节点,如上图中的3和6、5和9等都是兄弟节点。
树的分类:
二叉树,二叉搜索树,自平衡树,红黑树,完全树
在后面的内容中都会详细讲到
本章重点讲二叉搜索树
1.10.2 二叉树和二叉搜索树
二叉树
二叉树中的节点最多只能有两个子节点,一个是左子节点,一个是右子节点。左右子节点的顺序不能颠倒。因此,二叉树中不存在度大于2的节点。
二叉搜索树(BST——Binary Search Tree)是二叉树的一种,它规定在左子节点上存储小(比父节点)的值,在右子节点上(比父节点)存储大(或等于)的值。上图就是一个二叉搜索树。
根据二叉树的描述,一个节点最多只有两个子节点,我们可以使用《JavaScript数据结构——链表的实现与应用》一文中的双向链表来实现二叉搜索树中的每一个节点。下面是二叉搜索树的数据结构示意图:
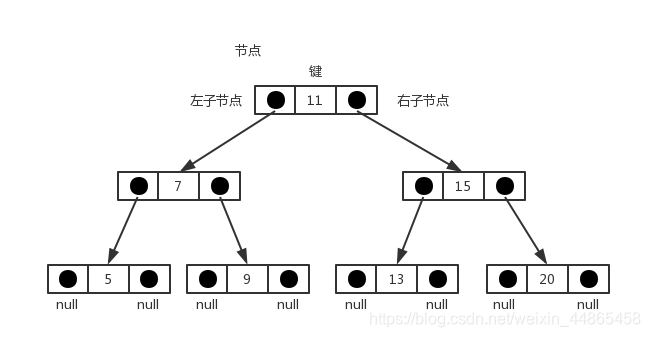
代码实现:
class BinarySearchTree {
constructor () {
this.root = null;
}
// 向树中插入一个节点
insert (key) {}
// 在树中查找一个节点
search (key) {}
// 通过中序遍历方式遍历树中的所有节点
inOrderTraverse () {}
// 通过先序遍历方式遍历树中的所有节点
preOrderTraverse () {}
// 通过后序遍历方式遍历树中的所有节点
postOrderTraverse () {}
// 返回树中的最小节点
min () {}
// 返回树中的最大节点
max () {}
// 从树中移除一个节点
remove (key) {}
}
在DoubleLinkedList类中,每一个节点有三个属性:element、next和prev。我们在这里用element表示树中节点的key,用next表示树中节点的右子节点(right),用prev表示树中节点的左子节点(left)。
insert (key) {
let newNode = new Node(key);
if (this.root === null) this.root = newNode;
else insertNode(this.root, newNode);
}
当树的root为null时,表示树为空,这时直接将新添加的节点作为树的根节点。否则,我们需要借助于私有函数insertNode()来完成节点的添加。在insertNode()函数中,我们需要根据新添加节点的key的大小来递归查找树的左侧子节点或者右侧子节点,因为根据我们的二叉搜索树的定义,值小的节点永远保存在左侧子节点上,值大的节点(包括值相等的情况)永远保存在右侧子节点上。下面是insertNode()函数的实现代码:
let insertNode = function (node, newNode) {
if (newNode.element < node.element) {
if (node.prev === null) node.prev = newNode;
else insertNode(node.prev, newNode);
}
else {
if (node.next === null) node.next = newNode;
else insertNode(node.next, newNode);
}
};
1.10.3 自平衡树(ALV树)
上面的BST树(二叉搜索树)存在一个问题,树的一条边可能会非常深,而其它边却只有几层,这会在这条很深的分支上添加、移除和搜索节点时引起一些性能问题。如下图所示:
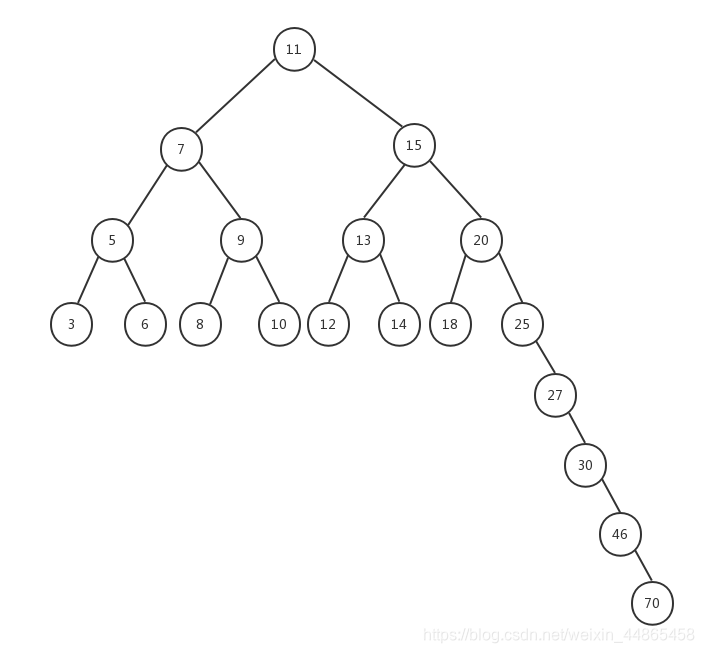
为了解决这个问题,我们引入了自平衡二叉搜索树(AVL——Adelson-Velskii-Landi)。在AVL中,任何一个节点左右两棵子树的高度之差最多为1,添加或移除节点时,AVL树会尝试自平衡。对AVL树的操作和对BST树的操作一样,不同点在于我们还需要重新平衡AVL树,在讲解对AVL树的平衡操作之前,我们先看一下什么是AVL树的平衡因子。
前面我们介绍过什么是树(子树)的高度,对于AVL树来说,每一个节点都保存一个平衡因子。
节点的平衡因子 = 左子树的高度 - 右子树的高度
观察下面这棵树,我们在上面标注了每个节点的平衡因子的值:
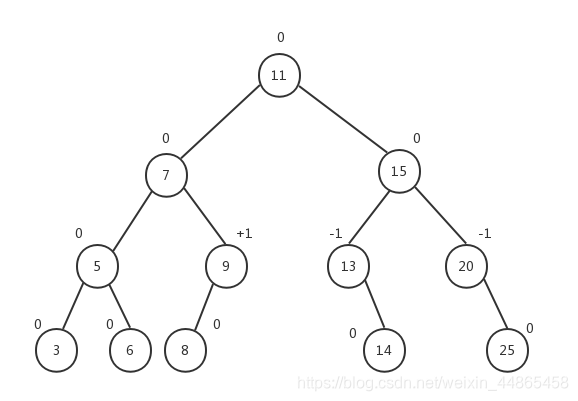
所有子节点的平衡因子都为0,因为子节点没有子树。节点5的左右子树的高度都为1,所以节点5的平衡因子是0。节点9的左子树高度为1,右子树高度为0,所以节点9的平衡因子是+1。节点13的左子树高度为0,右子树高度为1,所以节点13的平衡因子是-1…AVL树的所有节点的平衡因子保持三个值:0、+1或-1。同时,我们也注意到,当某个节点的平衡因子为+1时,它的子树是向左倾斜的(left-heavy);而当某个节点的平衡因子为-1时,它的子树是向右倾斜的(right-heavy);当节点的平衡因子为0时,该节点是平衡的。一颗子树的根节点的平衡因子代表了该子树的平衡性。
为了使AVL树重新达到平衡状态,我们需要对AVL树中的部分节点进行重新排列,使其既符合二叉搜索树的定义,又符合自平衡二叉树的定义,这个过程叫做AVL树的旋转。
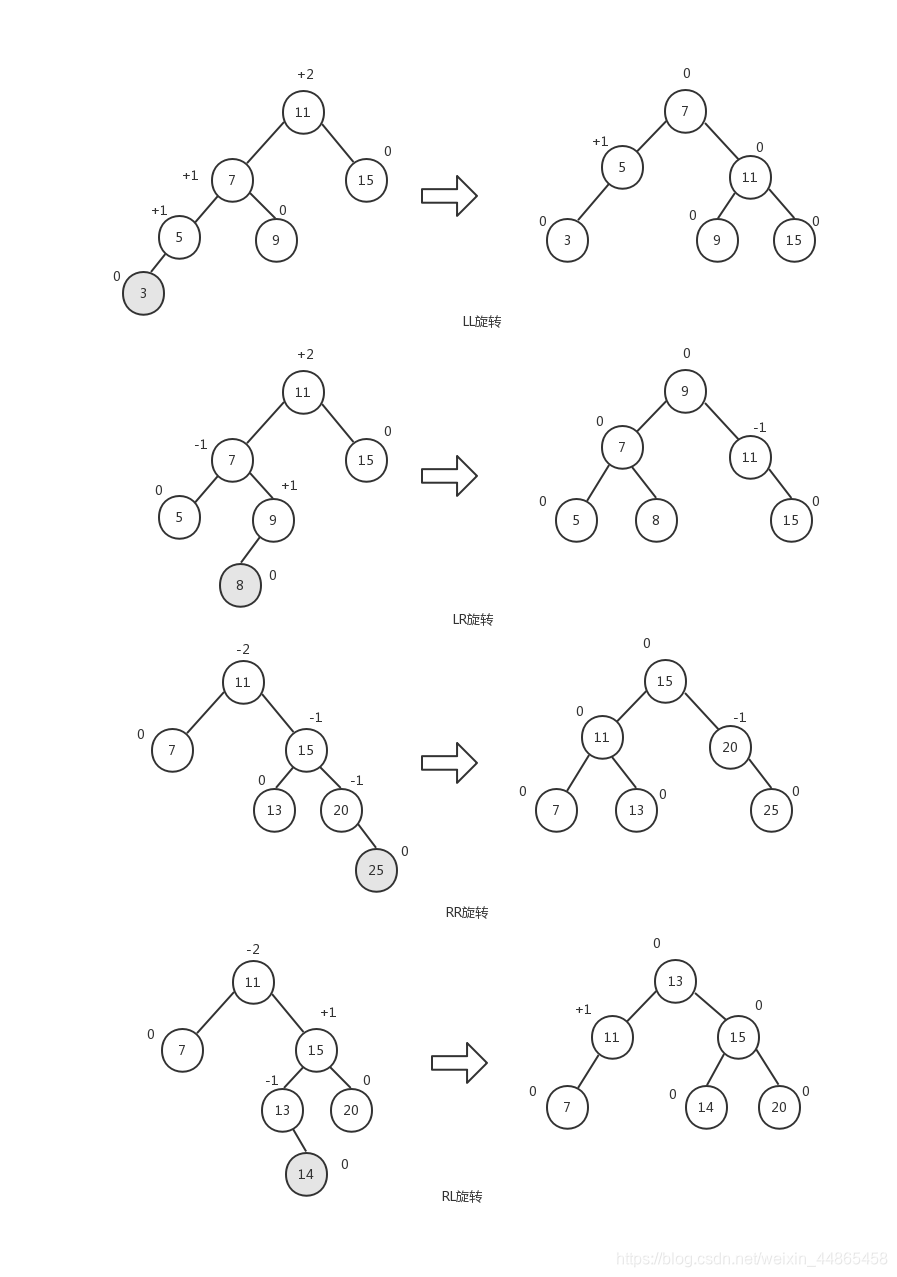
AVL树的旋转一共分为四种:
LL(left-left)旋转,新添加的节点位于树的根节点的左子树的左子树上。以非平衡因子的节点为中心将整棵树向右旋转。
LR(left-right)旋转,新添加的节点位于树的根节点的左子树的右子树上。先执行RR旋转,然后再执行LL旋转。
RR(right-right)旋转,新添加的节点位于树的根节点的右子树的右子树上。以非平衡因子的节点为中心将整棵树向左旋转。
RL(right-left)旋转,新添加的节点位于树的根节点的右子树的左子树上。先执行LL旋转,然后再执行RR旋转。
下面是这四种旋转的操作示意图:
红黑树
红黑树是一种平衡二叉树。这种树可以进行高效的中序遍历。通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束,确保没有一条路径会比其他路径长2倍,因而是近似平衡的。所以相对于严格要求平衡的AVL树来说,它的旋转保持平衡次数较少。用于搜索时,插入删除次数多的情况下我们就用红黑树来取代AVL
红黑树看的有点费劲,写不好,所大家就看这两篇文章吧:
javascript 红黑树算法与说明
树的三种遍历方式
前序遍历(NLR——Preorder Traversal)也叫先序遍历,先访问左子树,在访问根节点,最后访问右子树
口诀:左根右
中序遍历(LNR——Inorder Traversal),先访问根节点,后访问左子树和右子树
口诀:根左右
后序遍历(LRN——Postorder Traversal),先访问叶子及诶单。从左子树到右子树
左右根
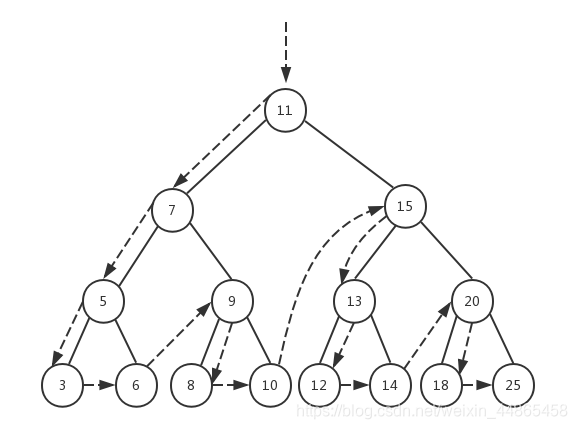
前序遍历:
中序遍历:
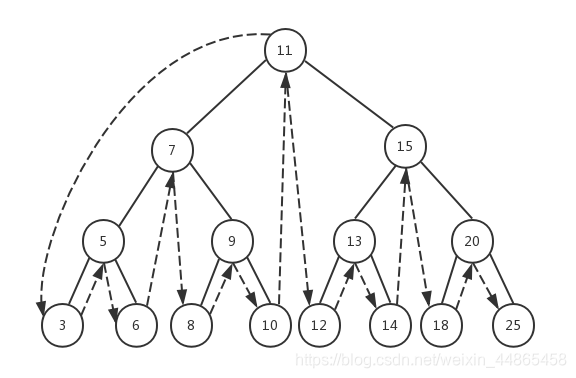
后序遍历:
代码实现:
// 前序遍历
let preOrderTraverseNode = function (node, callback) {
if (node !== null) {
callback(node.element);
preOrderTraverseNode(node.prev, callback);
preOrderTraverseNode(node.next, callback);
}
};
// 中序遍历
let inOrderTraverseNode = function (node, callback) {
if (node !== null) {
inOrderTraverseNode(node.prev, callback);
callback(node.element);
inOrderTraverseNode(node.next, callback);
}
};
// 后续遍历
let postOrderTraverseNode = function (node, callback) {
if (node !== null) {
postOrderTraverseNode(node.prev, callback);
postOrderTraverseNode(node.next, callback);
callback(node.element);
}
};
树的常用操作
搜索树中的最小值
搜索树中的最大值
搜索树中的特定值
删除节点
搜索树中的最小值
遍历左子树,找到最后一个子节点
代码实现:
let minNode = function (node) {
if (node === null) return null;
while (node && node.prev !== null) {
node = node.prev;
}
return node;
};
搜索树中的最大值
遍历右节点,直到找到最后一个子节点
代码实现:
`let maxNode = function (node) {
if (node === null) return null;
while (node && node.next !== null) {
node = node.next;
}
return node;
};`
搜索树中的特定值
第三种方式是搜索特定的值,我们需要比较要搜索的值与当前节点的值,如果要搜索的值小于当前节点的值,则从当前节点开始递归查找左子数(左子节点)。如果要搜索的值大于当前节点的值,则从当前节点开始递归查找右子树(右子节点)
代码实现:
let searchNode = function (node, key) {
if (node === null) return null;
if (key < node.element) return searchNode(node.prev, key);
else if (key > node.element) return searchNode(node.next, key);
else return node;
};
删除节点
如果删除的节点为叶子节点,则直接删除它
如果删除的节点只有一个子节点,则直接删除节点的父节点,指向其子节点
如果待删除的节点包含两个子节点,我们选择右子树上最小值创建一个临时子节点,然后复制到待删节点,然后删除最小子节点。
1.11二叉堆和堆排序
1.11.2二叉堆概述和特点
二叉堆是一种特殊的二叉树
也就是堆的数据结构,也叫做二叉堆,能高效的查找出最大值和最小值
常被应用于优先队列中,也经常被用在注明的堆排序算法中
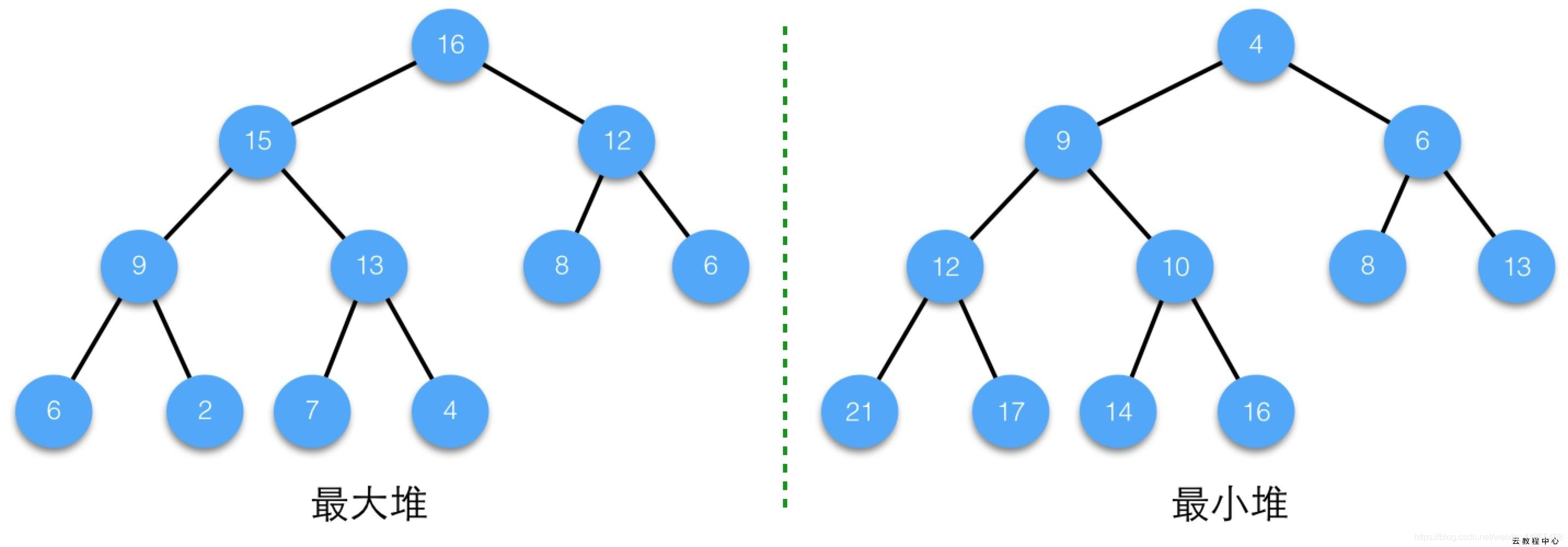
特点:
二叉堆是一颗完全二叉树,完全二叉树表示树的每一层都有左子树和右子树,(除了最后一层叶子节点),并且最后一层至少都哟一个左子树,
这叫结构特性
二叉堆不是最小堆就是最大堆,最小堆允许快速找出最小值,最大堆允许找出最大值,所有的节点都大于等于(最大堆)或小于等于(最小堆)的每个子节点,
这叫堆特性
1.11.3 二叉堆的实现
最小堆:
class MinHeap{
constructor() {
this.heap = []
}
// 替换两个节点值
swap(i1,i2){
const temp = this.heap[i1];
this.heap[i1] = this.heap[i2];
this.heap[i2] = temp;
}
// 获取父节点
getParentIndex() {
return (i -1) >> 1; //求除2的商
}
// 获取左节点
getLeftIndex() {
return i * 2 + 1; //求除2的商
}
// 获取右节点
getRightIndex() {
return i * 2 + 2; //求除2的商
}
// 上移
shiftUp(index) {
if(index == 0) {return;}
const parentIndex = this.getParentIndex(index);
if(this.heap[parentIndex] > this.heap[index]) {
this.swap(parentIndex,index);
this.shiftUp(parentIndex);
}
}
// 下移
shiftDown() {
const leftIndex = this.getLeftIndex(index);
const rightIndex = this.getRightIndex(index);
if(this.heap[leftIndex] < this.heap[index]) {
this.swap(leftIndex,index);
this.shiftDown(leftIndex);
}
if(this.heap[rightIndex] < this.heap[index]) {
this.swap(rightIndex,index);
this.shiftDown(rightIndex);
}
}
// 插入
insert(value) {
this.heap.push(value);
this.shiftUp(this.heap.length - 1);
}
// 删除堆顶
pop() {
this.heap[0] = this.heap.pop();
this.shiftDown(0);
}
// 获取堆顶
peek() {
return this.heap[0];
}
// 获取堆的大小
size() {
return this.heap.length;
}
}
const h = new MinHeap();
h.insert(3);
h.insert(2);
h.insert(1);
h.pop();
参考代码:
JavaScript 实现:最小堆类
最大堆:
let heap = [];
function swap(index1, index2) {
let temp;
temp = heap[index1];
heap[index1] = heap[index2];
heap[index2] = temp;
}
function shiftup(index) {
let parentIndex = (index - 1) >> 1// Math.floor((index - 1) / 2);
if (index != 0 && heap[parentIndex] < heap[index]) {
swap(parentIndex, index);
shiftup(parentIndex);
}
}
function shiftDown(index) {
let leftNodeIndex = (index + 1) * 2 - 1, rightNodeIndex = (index + 1) * 2
if (leftNodeIndex < heap.length && heap[leftNodeIndex] > heap[index]) {
swap(leftNodeIndex, index);
shiftDown(leftNodeIndex);
} else if (rightNodeIndex < heap.length && heap[rightNodeIndex] > heap[index]) {
swap(rightNodeIndex, index);
shiftDown(rightNodeIndex);
}
}
function insert(val) {
heap.push(val);
shiftup(heap.length - 1);
}
function remove() {
swap(0, heap.length - 1);
heap.pop();
shiftDown(0);
return heap[0];
}
insert(1);
insert(3);
insert(2);
insert(5);
remove();
insert(4);
insert(6);
remove();
console.log(heap);//[ 4, 3, 2, 1 ]